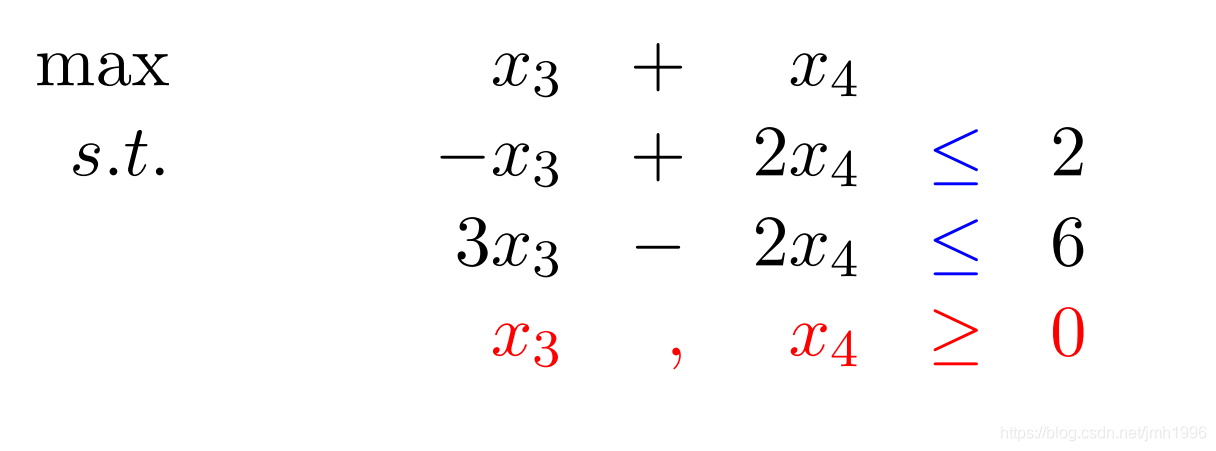线性规划，以前一直小瞧它了，它其实一种特别表达能力特别强的工具，只要能够将问题定义成线性规划的问题，那么就可以使用单纯形法来解决。

为什么说，线性规划的表达能力很强呢？因为像经典的网络流算法、最小费用流算法、多物品流算法都可以写成线性规划的形式，一旦划归成线性规划，那么就可以使用单纯形法在平滑多项式的时间内解决问题。至于如何划归成线性规划问题就是看个人的本事了，看个人的创造力了，近几年也的确有人尝试将原先复杂度极高的问题转换成线性规划问题后，使问题得到多项式时间内的解决。

单纯形算法是求解线性最优化问题的超级有效的算法，本文就来看看这个单纯形算法是如何导出的。

线性规划的几种形式

线性规划的一般形

线性规划是指目标函数、约束条件都是线性的最优化问题。
线性规划问题会有含有 $n$ 个自变量： $X=(x_{1},x_{2},x_{3},\dots,x_{n})^{T}$ ，
一个目标函数： $obj(X)=c_{1}x_{1}+c_{2}x_{2}+\dots+c_{n}x_{n}$ ,写成矩阵的形式就是 $obj(X)=C^{T}X$ 。这表示目标函数是自变量的线性函数，然后问题是最大化或者最小化这个目标函数： $min$ $obj(X)$ 或 $max$ $obj(X)$
然后会有一堆的线性约束：
一些等式约束： $a_{i}^{T}X=b_{i}$
一些不等式约束： $a_{j}^{T}X<=b_{j}$ 或者 $a_{k}^{T}X>=b_{k}$

上面描述就是线性规划的一般形，特指它的约束里面既有等式约束又有不等式约束，目标既可以最大化又可以最小化。
这种表达很自然，但是不适于用计算机处理。于是有学者提出了线性规划的标准型。

线性规划的标准型

线性规划的标准型，是从一般型转换而来，转换的目标是把最优化都转为最小化，然后把无约束、等式约束、不等式约束都转换为小等于约束，以及把每个变量约束到非负。
线性规划的标准型为：
$min \space C^TX$
$s.t.\space AX<=b,X>=0$
其中， $A \in R^{m\times n}，b \in R^{m},X\in R{^n}$
那么如何把一般型转成标准型呢？

把目标函数由最大化转最小化：假如原问题目标是 $max\space obj(X)$ ，那么最大化 $obj(X)$ 就是在最小化 $- obj(X)$ 。
把等式约束改成小于等于约束：假如原问题存在某个等式约束： $a_{i*}X=b_{i}$ ,其中 $a_{i}$ 是约束矩阵 $A$ 的第 $i$ 行。那么可以把这个等式约束转换为两个不等式约束： $a_{i*}X<=b_{i}$ 以及 $-a_{i*}X<=-b_{i}$ 。
把大等于约束改成小等于约束：假如原约束为 $a_{j*}X>=b_{j}$ ,那么两边同乘负号转为： $-a_{j*}X<=-b_{j}$
把无约束改成小等于约束：假如一般型里面有某个变量 $x_{k}$ 的约束是 $x_{k}\in R$ ，那么构造两个新变量： $x'_{k},x''_{k}$ 要求 $x'_{k}>=0,x''_{k}>=0$ 。令 $x_{k}=x'_{k}-x''_{k}$ ，然后把线性规划里面所有的 $x_{k}$ 都拿 $x'_{k}-x''_{k}$ 替换。

线性规划的松弛型

转换为标准型后，线性规划问题就已经很好描述了，但是它不是很好实现，一般人们更愿意看到等式约束，于是再把标准型转成松弛型。主要是把标准型里面的小等于约束，通过添加松弛变量的方法，把它们转为等式约束。
转换的方法为：
对于标准型的小等于约束： $a_{i*}X<=b_{i}$ 。通过添加松弛变量 $x_{n+1}>=0$ ,使得 $a_{i,1}x_{1}+a_{i,2}x_{2}+a_{i,3}x_{3}+\dots+a_{i,n}x_{n}+x_{n+1}=b_{i}$ 。这里需要松弛变量 $x_{n+1}$ 非负，才能满足原来条件。
经过这些变换，最终我们会得到线性规划的松弛型：
$min \space C^TX$
$s.t.\space AX=b,X>=0$
这种形式就很棒啦。

转换的例子

这里举一个线性规划由一般型转标准型，再由标准型转松弛型的例子。
一般型：
在这里插入图片描述
转换标准型：

在这里插入图片描述

转换为松弛型：
在这里插入图片描述

单纯形法的导出

通过一定的转换后，线性规划的可以转换为松弛型：
$min \space C^T X$
$s.t. \space AX=b,X>=0$
其中，X是一个n维的列向量 $X=(x_{1},x_{2},\dots,x_{n})$ 表示n个自变量。 $C^{T}$ 也是n维列向量， $A$ 是 $m\times n$ 的矩阵表示m个约束。一般我们会假设 $rank(A)=m<n$ ，表示给出的m个约束条件都是有效的，否则可以通过行初等变换把0行去掉。

可行解对应了一个多胞体

约束条件里面的 $AX=b$ 是我们都很熟悉的线性方程组，因为这个 $rank(A)=m<n$ ,因此 $AX=b$ 必定有解，而且通解的形式应该是一个 $AX=b$ 的特解加上 $AX=0$ 的通解。因为 $AX=0$ 通解包含 $n-m$ 个自由量，那么 $\{X|AX=b\}$ 其实就是一个自由度为 $n-m$ 的向量空间。同时这也说明了 $A$ 中线性无关的列的数目是 $m$ 。当通解里面的自由变量的解确定了，那么完整的解也就是确定了，因此虽然 $X \in R^{n}$ ，但是它的自由度是 $n-m$ 。

而 $X>=0$ ,说明了各个分量不得非负，这就要求自由量非负，同时这些自由量决定的非自由量也是非负的。这就会对 $\{X|AX=b\}$ 加上一定的限制。
我们先把 $A$ 的 $m$ 个线性无关的列放挪前m列，然后x要做相应的转换，我们假设已经转换好了，x也对应好了。
然后对 $AX=b$ 展开：
$a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+\dots+a_{1m}x_{m}+\dots+a_{1n}x_{n}=b_{1}$
$a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+\dots+a_{2m}x_{m}+\dots+a_{2n}x_{n}=b_{2}$
$\dots$
$a_{m1}x_{1}+a_{m2}x_{2}+a_{m3}x_{3}+\dots+a_{mm}x_{m}+\dots+a_{mn}x_{n}=b_{m}$
经过高斯消元后，前m列可以化成一个 $m \times m$ 的单位阵，即：

$x_{1}+0x_{2}+0x_{3}+\dots+0x_{m}+a'_{1,m+1}x_{m+1}\dots+a'_{1,n}x_{n}=b'_{1}$
$0x_{1}+x_{2}+0x_{3}+\dots+0x_{m}+a'_{2,m+1}x_{m+1}\dots+a'_{2,n}x_{n}=b'_{2}$
$\dots$
$0x_{1}+0x_{2}+0x_{3}+\dots+x_{m}+a'_{m,m+1}x_{m+1}\dots+a_{m,n}x_{n}=b'_{m}$
于是，后面的n-m个未知数就是自由变量了，现在要求每个变量都要非负：于是： $x_{1}>=0,x_{2}>=0,\dots,x_{n}>=0$ 。把前面m个变量当做松弛变量，那么这其实就可以转换对这n-m个自由变量的约束：
$a'_{1,m+1}x_{m+1}\dots+a'_{1,n}x_{n}<=b'_{1}$
$a'_{2,m+1}x_{m+1}\dots+a'_{2,n}x_{n}<=b'_{2}$
$\dots$
$a'_{m,m+1}x_{m+1}\dots+a_{m,n}x_{n}<=b'_{m}$
同时各个自由量非负。
因为n-m个自由变量确定后，m个基本量就可以唯一确定，因此现在我们来单独考察这n-m个自由变量的性质。
这n-n个自由变量构成了一个n-m维的向量空间。
这些约束里面的每个约束 $a'_{i,m+1}x_{m+1}\dots+a'_{i,n}x_{n}<=b'_{i},i\in [1,2,3,···,m]$ 都构成了一个n-m维向量空间的半超平面 $HS_{i}$ ，什么意思呢？
例如： $x_{1}+x_{2}+x_{3}<=3$ ，就是用 $x_{1}+x_{2}+x_{3}=3$ 这个超平面把 $R^3$ 空间分成两半，我们需要的是小于3的那一半。

于是最终的可行解 $Solution$ 就是由这m个约束以及n个非负约束构成的半平面的交集了,即 $Solution=\bigcap^{n}_{i=1}HS_{i}$ 。而这个可行解空间就构成了一个所谓的多胞体。

注意一点就是现在我们研究的对象是那n-m个自由变量，因为剩下的m个基本量在这些自由变量确定后会被唯一确定的。

我们把上面的过程用一个具体的例子来体现。
假设一个线性规划为：
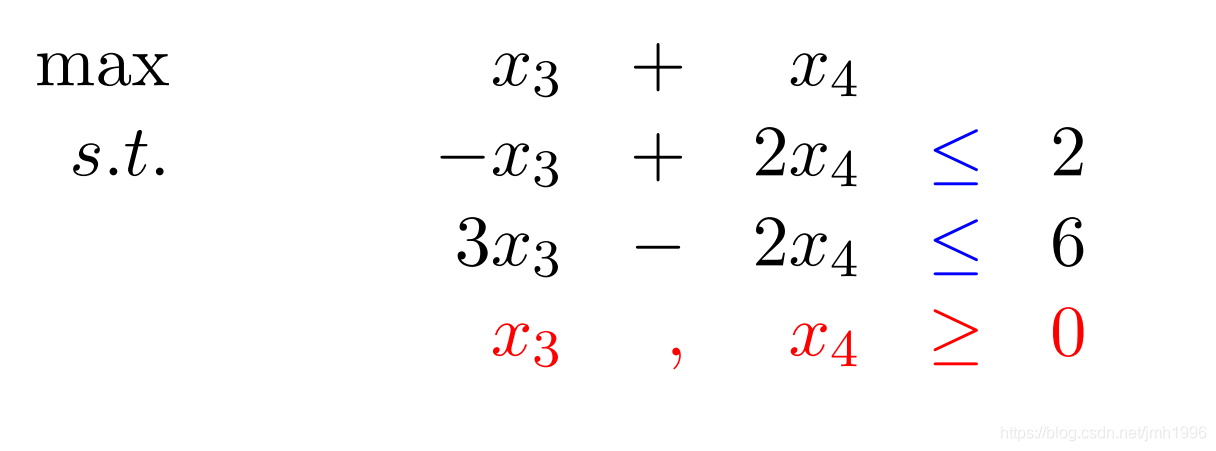
在这里插入图片描述
它的松弛形式为：
$min \space -x_{3}-x_{4}\space$
s.t.
$x_1\space -x_{3}+2x_{4}=2$
$\space x_{2} \space +3x_{3}-2x_{4}=6$
$x_1>=0,x_2>=0,x_3>=0,x_4>=0$
那么于是可以把 $x_{3},x_{4}$ 当做自由变量，当它们的值确定后 $x_{1},x_{2}$ 也就确定了。
最终这些约束下构成的可行解为：
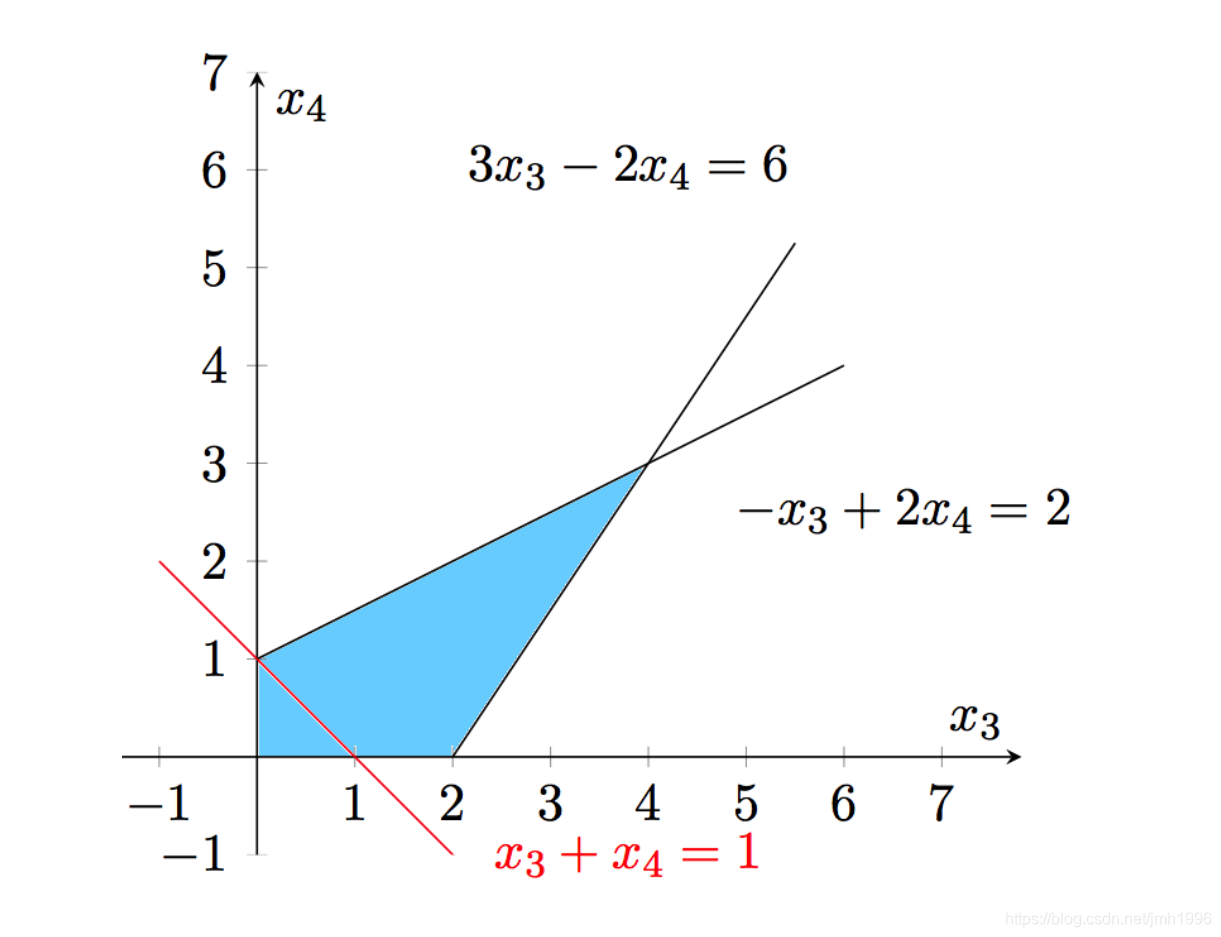
在这里插入图片描述

最优解可以在多胞体的顶点获得

我们知道可行解是由多个半平面的交集构成的，因此这些半平面的交点就构成一个个的顶点，本节需要说明的就是目标函数的最优值一定可以在某个顶点取得（如果存在的最优解的话）。
例如，上面的例子
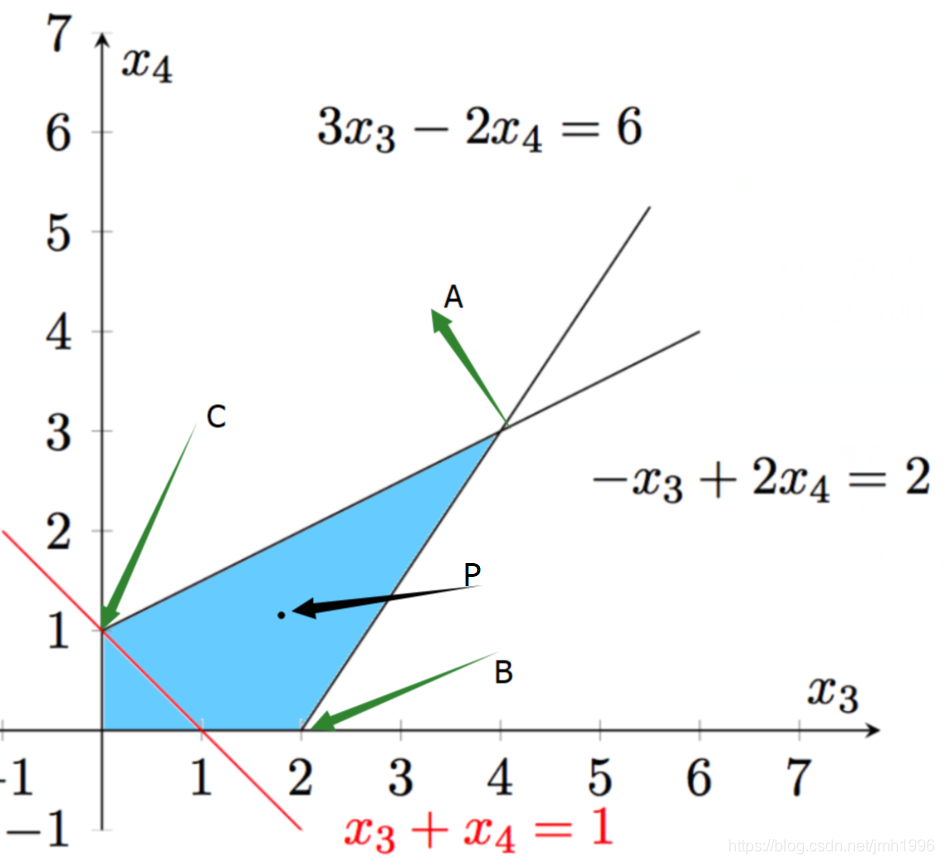
在这里插入图片描述
假设目标函数的最小值是在这个多边形区域的 $P$ 点取得的。
那么因为P是在四边形 $OBAC$ 内部，那么一定存在非负的 $\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4}$ ,且 $\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}=1$ ，使得： $P=\lambda_{1}O+\lambda_{2}B+\lambda_{3}A+\lambda_{4}C$ 。

于是： $c^TP=\lambda_{1}c^TO+\lambda_{2}c^TB+\lambda_{3}c^TA+\lambda_{4}c^T C$
取这四部分最小的那个 $t=min(c^TO,c^TB,c^TA,c^T C)$
$c^TP>=\lambda_{1}t+\lambda_{2}t+\lambda_{3}t+\lambda_{4}t=t$

===>在某个顶点出找到一个最起码不会更差的最优解。
因此，最优解一定可以某个顶点取得。
于是，在计算最优解的时候，我们无须计算可行解里面的所有解，只需要计算那些顶点的最优解即可。
至此，问题就转而如何求这个多胞型的顶点的问题了。

如何找到顶点

首先，我们得先给出一个多胞型里面顶点的准确定义。那上面的四边形做例子：
在这里插入图片描述
一共有四个顶点，这些顶点的特征是什么呢？他们都不在这个多边形内任意两点构成的线段里面。形式化的表达就是：四边形内不存在 $P_1,P_2$ 两个点，使得 $O=\lambda_{1}P_1+\lambda_2 P_2$ ,其中 $\lambda_1+\lambda_2=1,\lambda_1>0,\lambda_2>0$ 。

OK,理清这一点后，我们就要指出下面这个定理了。
多胞体里面的每个顶点对应着由A的某组基本列，这组基确定了这个顶点的坐标。
先说说啥是基本列。上面说到 $A \in R^{m \times n}$ ,而且 $rank(A)=m<n$ 。于是矩阵A里面线性无关的列的个数就是 $m$ 。一组线性无关的列，就构成了矩阵 $A$ 的基本列。

我们假设矩阵 $A$ 的基本列的下标是 $i_{1},i_{2},i_{3},\dots,i_{m}$ ，表示第 $i_{1},i_{2},i_{3},\dots,i_{m}$ 列构成m个无关向量。

因为 $AX=b$ ,这个式子含义是A的所有列按照 $X$ 为系数的线性组合构成了b。因此有： $b=\vec a_{*1}x_{1}+\vec a_{*2}x_{2}+\vec a_{*3}x_{3}+\dots+\vec a_{*n}x_{n}$ ,其中 $a_{*j}$ 表示第j列。
我们把那些基本列表示出来：
$b=\vec a_{*1}x_{1}+\vec a_{*2}x_{2}+\dots+\vec a_{*i_{1}}x_{i_{1}}+\vec a_{*j}x_{j}+\dots+\vec a_{*i_{k}}x_{i_{k}}+\dots+\vec a_{*i_{m}}x_{m}+\dots+\vec a_{*n}x_{n}$ .

现在，基于第 $i_{1},i_{2},i_{3},\dots,i_{m}$ 列构成m个无关向量，我们构造一个特殊的解。

既然第 $i_{1},i_{2},i_{3},\dots,i_{m}$ 列构成m个线性无关向量，于是这些向量就已经足够来表出 $b$ 。于是，我们让基本列以外的列的系数设置为0，然后指定由这组基本列来表出b。
即：
$b=\vec a_{*1}0+\vec a_{*2}0+\dots+\vec a_{*i_{1}}x_{i_{1}}+\vec a_{*j}0+\dots+\vec a_{*i_{k}}x_{i_{k}}+\dots+\vec a_{*i_{m}}x_{m}+\dots+\vec a_{*n}0$ 让那些 $x_{i}=0,i \not \in \{ i_{1},i_{2},i_{3},\dots,i_{m} \}$ 。

举个例子，如果矩阵A有7列，它的1,3,5,6列构成一组基本列。那么就让 $x_{2}=x_{4}=x_{7}=0$ ，而 $b=a_{*1}x_{1}+a_{*3}x_{3}+a_{*5}x_5+a_{*6}x_6$ 。

因为第 $i_{1},i_{2},i_{3},\dots,i_{m}$ 列构成m个无关向量，那么通过它们来线性表出 $b$ 的方式就是唯一的。
这是因为,我们把这组基本列堆在一起构成的矩阵 $B=(a_{*i_{1}}|a_{*i_{2}}|···|a_{i_{m-1}}|a_{i_{m}}|)$ 是一个 $m\times m$ 的满秩矩阵。那么 $BX'=b$ 当然就只有唯一的解： $X'=B^{-1}b$ ，当然我们得要求 $X'>=0$ ,如果不满足条件就话再换一组基本列。

我们会发现，这个 $X'$ 配上各个的m个0 所构成的解 $X=(0,0,0,\dots,x'_1,··· x'_2···，x'_m···)$ 就是解空间的那个多胞体的顶点。

这是因为，假设这个构造的 $X$ (含有n-m个0)的点不是顶点，那么它必然可以在解空间内某两个点形成的线段的内部：即存在不同 $X^{(1)},X^{(2)}$ ，使得 $X=\lambda X^{(1)}+(1-\lambda)X^{(2)}$ ,其中： $0<=\lambda<=1,AX^{(1)}=b,AX^{(2)}=b,X^{(1)}>=0,X^{(2)}>=0$ 。
显然，对于那么 $X$ 中为0的分量， $X^{(1)}和X^{(2)}$ 对应的分量也为0。于是 $X^{(1)},X^{(2)}$ 和 $X$ 一样，有n-m个0，剩下m个分量作为基本列的系数去线性表出 $b$ 。于是 $X=X^{(1)}=X^{(2)}$ ，这就导致了矛盾。
==>说明 $X$ 是顶点。
其实，这也是说明了一点：含有m-n个0的解，一定对应于多胞体的某个顶点。

通过这种方式，我们就已经构造出了一个顶点了。

只得到一个顶点显然是不够的，虽然我们知道最优值在顶点取得，但是具体在那个顶点是不得而知的，我们得不断的尝试。

解决了如何找顶点的问题，现在的问题就是如何由当前顶点，构造出另外一个顶点了。这点由下篇博客给出。

线性规划专题——SIMPLEX 单纯形算法（一）