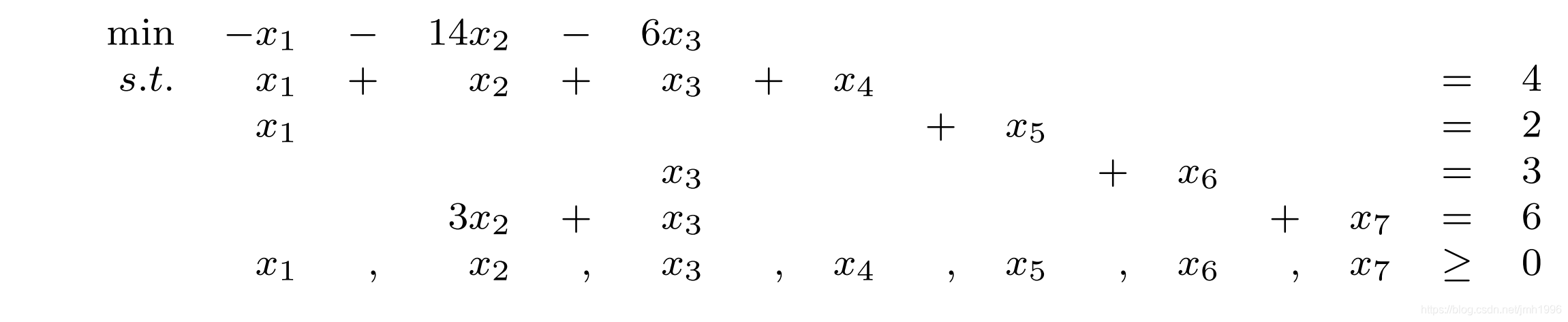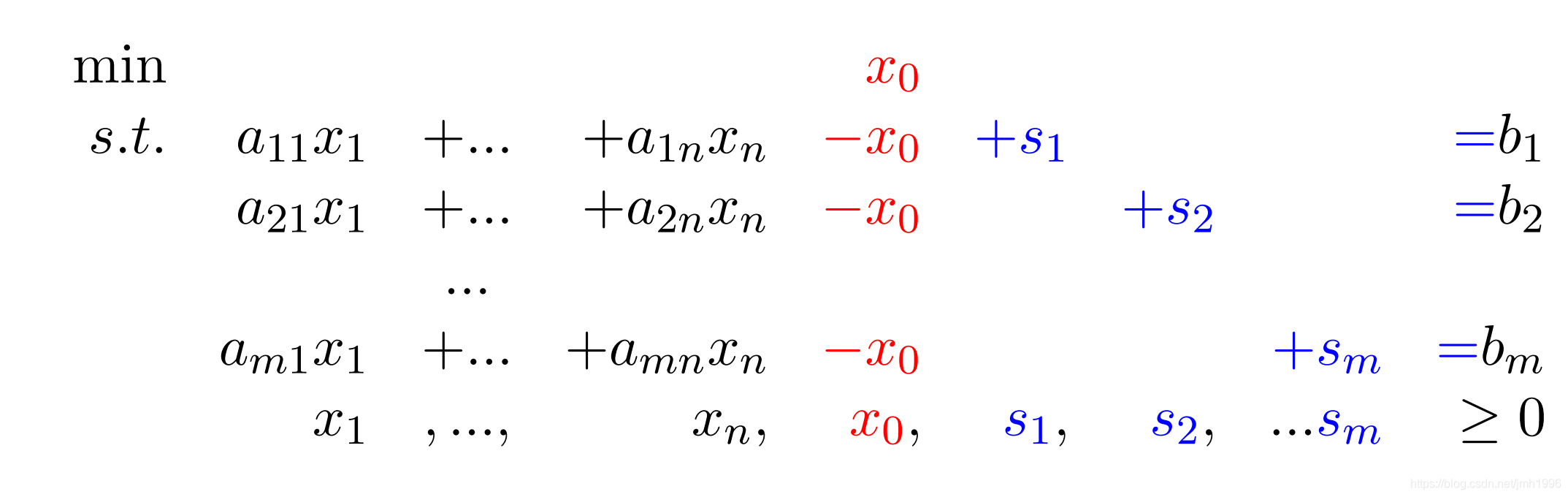线性规划专题——SIMPLEX 单纯形算法（二）

版权声明：本文为博主jmh原创文章，未经博主允许不得转载。 https://blog.csdn.net/jmh1996/article/details/85010037

前言

线性规划专题——SIMPLEX 单纯形算法（一) 提到了在线性规划问题的以下结论：

1. 问题的所有可行解构成了一个n-m维度的多胞型
2. 而且最优解会在多胞型的顶点取得。
3. 每个顶点对着系数矩阵的一组基，或者系数矩阵的每组基对应着一个顶点。
4. 同时我们给出了多边形或者更一般的多胞型的顶点的定义：顶点是那些特殊点，对于这些点而言，无法找到多边形内部两个不同的点，使得顶点在这两个内部点形成的线段内。同时我们给出了多边形或者更一般的多胞型的顶点的定义：顶点是那些特殊点，对于这些点而言，无法找到多边形内部两个不同的点，使得顶点在这两个内部点形成的线段内。
   
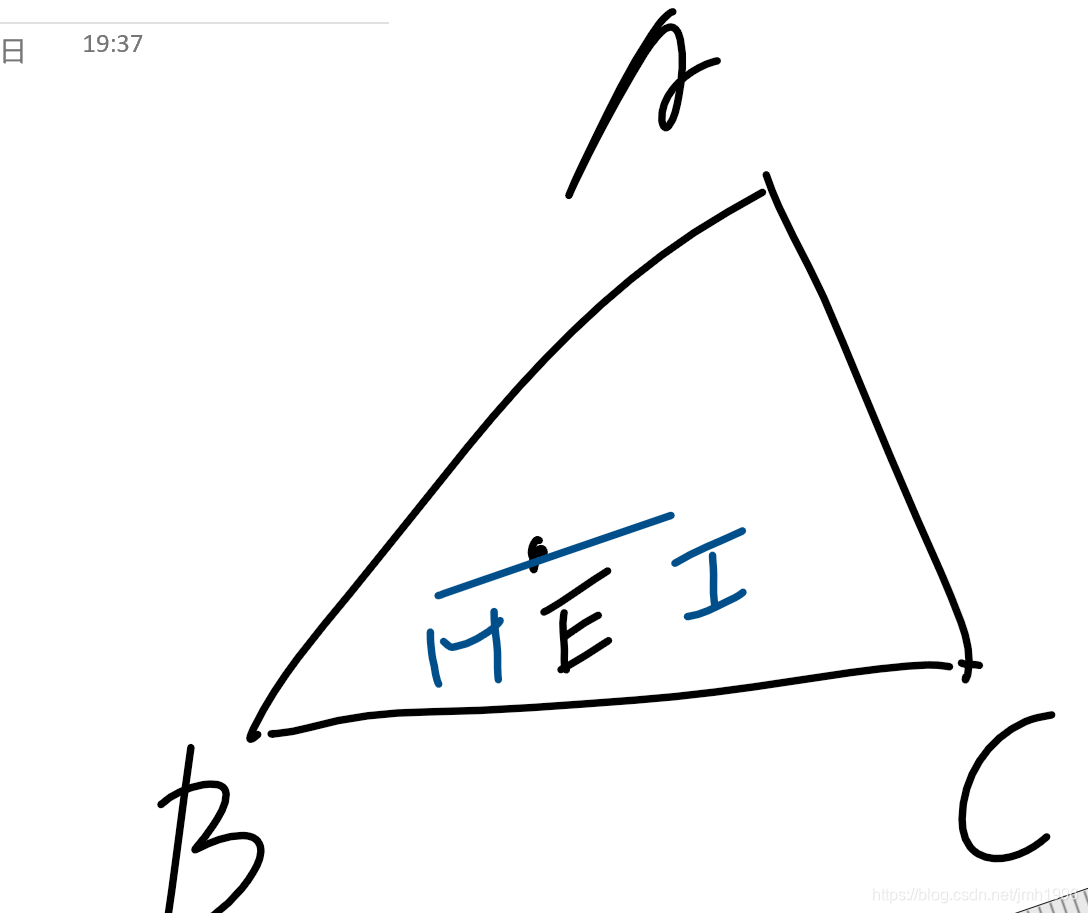
   例如上面这个多边形里面，A,B,C是顶点，这三个点就不在任何多边形内点所形成的线段内部。而E不是顶点，那么总是可以找到任意多条线段使得E在线段的内部。
5. 顶点的解的格式：对于一个 $m \times n$的系数矩阵 $A$来说，且 $rank(A)=m$,它表示 $m$约束， $n$个未知数。那么这个系数矩阵内每组基含有 $m$线性无关的列。顶点的解的格式：至少 $n-m$个0，剩下每一个 $x_{i}$都对应着矩阵 $A$的第 $i$列选为基本列下的解。

OK，本章就来解决单纯型法剩下的几个问题。

1. 如何从一个顶点转移到另外一个顶点？
2. 什么时候单纯型算法停止？
3. 如何生成第一个可行解，或者可行顶点？

如何从一个顶点转移到另外一个顶点？

假设对于如下化为松弛型的线性规划：

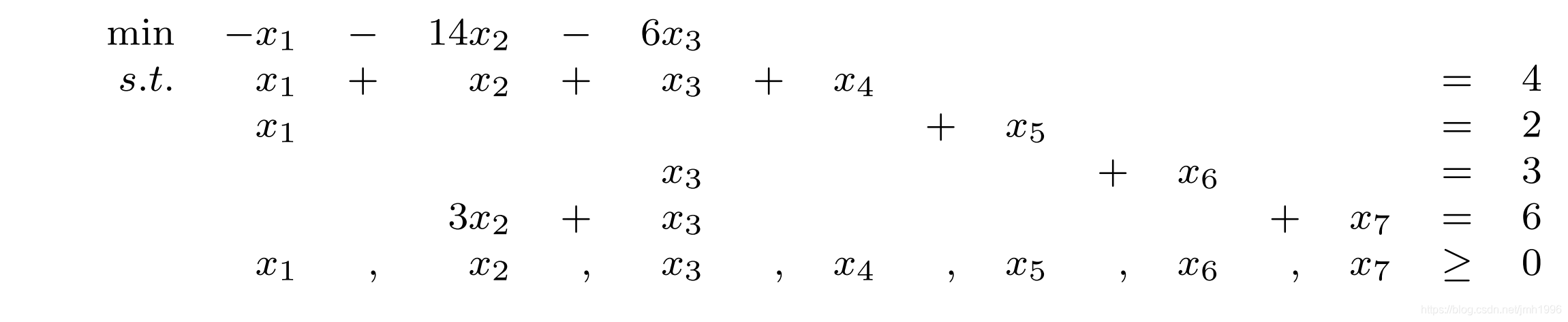
我们提取出它的系数矩阵，并且找到它的一个顶点。

这个顶点是： $X=[2,0,0,2,0,3,6]$，注意这里的蓝色的 $x_{i}$。他们的值不为0，那么他们对应的列：第1列，第4列，第6列，第7列构成了系数矩阵的一组基。

现在，我们从 $x$出发，构造出一个新的顶点出来。
因为每组顶点都对应这一组基，于是这个问题就等价于从原来由第1列、第4列、第6列、第7列形成的一组基构造出一个新的基来。

我们知道，这个系数矩阵是包含了 $n$列的，在示例中就是7列，而这个矩阵的rank，又是 $m$,也就是4。因此，为了构造一个新的基，我们只要把旧的那组基本列里面换下一列，然后从原来非基本列里面选出一列放进去就又形成了一组基。

例如，现在我们想把系数矩阵的第三列放进来。那么应该把旧基本列里面那个列踢出去呢？

第三列本来是不属于基本列的，那么第三列肯定是可以由旧的基：第2列、第4列、第5列、第6列线性表出的。

下面，我们用 $A_{*i}$表示矩阵A的第i列, $A_{j*}$ 表示矩阵A的第j行。

显然 $(A_{*1},A_{*4},A_{*6},A_{*7})$构成了 $A$的基本列，因为他们正好是一个元素个数为4的线性无关组。
于是 $A_{*3}$必然可以由这组基本列线性表出。怎么计算系数呢？

假设 $A_{*3}=\lambda_1A_{*1}+\lambda_4A_{*4}+\lambda_5A_{*6}+\lambda_7A_{*7}$,把 $A_{*1},A_{*4},A_{*6},A_{*7}$并排在一起形成一个新的矩阵，那么这可以写成矩阵的形式：
$(A_{*1}|A_{*4}|A_{*6}|A_{*7})(\lambda_1,\lambda_2,\lambda_6,\lambda_7)^T=A_{*3}$
解这个线性方程组就是了。最后可以解的： $A_{*3}=0A_{*1}+1A_{*4}+1A_{*6}+1A_{*7}$,

于是两边同时减去 $A_{*3}$得到：
$0=-A_{*3}+0A_{*1}+1A_{*4}+1A_{*6}+1A_{*7}$
我们整理一下，按列下标递增的方式写一下：
$0A_{*1}+0A_{*2}-1A_{*3}+1A_{*4}+0A_{*5}+1A_{*6}+1A_{*7}=0$
把它写成矩阵的形式就是说：
$A(0,0,-1,1,0,1,1)^T=0$
令 $\vec\lambda=(0,0,-1,1,0,1,1)$，那么就是 $A\vec\lambda^T=0$

那么，这意味这什么？？？？？？？
那么，这意味这什么？？？？？？？
那么，这意味这什么？？？？？？？

我们线性规划的约束条件不就是：

1. $AX=\vec b$
2. $X>=0$

对于当前的一个顶点 $X=[2,0,0,2,0,3,6]$，考虑 $X'=X+\theta\vec\lambda$，那么 $AX'^T=A(X^T-\theta \vec \lambda)=AX^T-\theta A \vec \lambda=\vec b+\vec 0$。其中 $\theta>=0$。

这就是说明， $X'$最起码天然的满足第1个约束条件。当 $X'$恰好都非负的时候，它也满足第二个约束条件了，此时 $X'$就是可行域上面的一个可行解。

但是，别忘了我们的目标是什么：为了构造出另外一个顶点出来。因此， $X'$仅仅是个可行解还不够，我们还得想办法让它成为顶点才行。

那么顶点的特征是什么？通过上一篇博客，我们晓得了，顶点的特征是：至少具有n-m个0，这n-m的分量对应了n-m个非基本列；剩下m个分量对应了m个基本列。

于是，我们可不可以想办法让 $X'$也具有这个的特点？
$X'=X-\theta \vec \lambda$
注意到：

1. $X=[2,0,0,2,0,3,6]$
2. $\vec \lambda=[0,0,-1,1,0,1,1]$

我们慢慢的增大 $\theta$的值,得到下面的表格：

$\theta$	$X'=X-\theta \vec \lambda$
0.1	$[2,0,0.5,1.5,0,2.5,5.5]$
1	$[2,0,1,1,0,2,5]$
2	$[2,0,2,0,0,1,4]$
3	$[2,0,3,-1,0,0,3]$

当 $\theta=0.5或1$的时候，得到 $X'$的确是可行解，但是却不是顶点。
当 $\theta=2$的时候，得到的 $X'$刚好是可行解，也是顶点。
当 $\theta=3$的时候，得到的 $X'$就是可行解，因为它有一个分量都小于0。

于是，当 $\theta=2$的时候，得到的 $X'=[2,0,2,0,0,1,4]$ 就是我们需要的顶点。

我们观察一下，这个顶点里面第1,3，6,7项不为0，剩下3项为0.这就意味着这个顶点对应的基本列是 第1列、第3列、第6列、第7列。
跟原来的那组基本列相比，恰好把第4列换下来了，把第3列换上去了。

我们要注意，我们不仅可以选择第3列，还可以选择第2列，第5列换上去。但是，不管我们是从这三列中选的那一列，当要换上去的列确定后，旧的基本列要换下谁也就确定了。

例如，这里换上去的第3列是我们自己选择的，当我们选择这列后，被换下来的第4列是计算得到的：它是随着 $\theta$增大，那些基本列对应的 $X'$的分量中首先到达0的那个列。

至于，到底要选那一列，我们可以选择使得目标函数减少最大的那个那一列换入。

总结一下，如何从一个顶点切换到另外一个顶点。

1. 从当前顶点得到的解 $X$，找出对应的基本列。
2. 然后从非基本列里面随便选一个列出来，把它当做是将来要换上去成为新的基本列的列。
3. 用第一步的基本列去表示第二步选择的非基本列，求到它们的系数。构造一个向量 $\vec \lambda$,使得 $A\vec \lambda=\vec0$，而且 $\vec \lambda$不全为0。
4. 寻找最小的非负 $\theta$,使得 $X'=X-\theta \vec \lambda$ 是顶点。其实 $\theta=min\frac{x_{i}} {|\vec\lambda_{i}|}$。

如果很不幸，在4步 $\theta$为0 那么很容易进入死循环。如果 $\theta$全部是无穷大，这意味着可行域是无界的。

什么时候单纯型算法停止呢？

解决如何从一个顶点转移到另外一个顶点的时候，如何存在有好多可以换入的列，我们会选择使得目标函数减少最多的那一列换入。

记 $X'=X-\theta \vec \lambda$，于是目标函数的优化量： $\Delta=C^TX'^T-C^TX^T=C^T(X'^T-X)=-\theta C^T\vec \lambda^T$

• 当对于任意的非基本列，把它换进去以后，如果目标函数的优化量 $\Delta$都是大于等于0的话，说明换入任何新的一列，目标函数都不再减少了，此时当然就到达最优解了。算法可以终止了。

• 当 $\Delta$大于等于 0 的时候， $\theta C^T \vec \lambda^T$是小于等于0的。有因为 $\theta>=0$，所以 $C^T\vec \lambda^T$小于等于 0 。 $\vec \lambda$ 是用旧的基本列来表示当前需要换入的列的“系数”,它只有要换入的那个列对应的元素为-1，其他元素都是非负的。
  于是 $C^T\vec \lambda^T=-c_{e}+\sum_{i \not \in {e}} c_{i}\lambda_{i} <=0，e$是要换入的列的列号。两边同乘-1，于是有： $c_{e}-\sum_{i \not \in {e}} c_{i}\lambda_{i} >=0，For \space every \space e.$

• 反之，若存在某个非基本列，使得加入它后得到的目标函数优化量 $\Delta$是小于0的，说明目标函数还可以优化，于是就把这个非基本列换进来。

形式化的来说就是：

这是因为：

如何生成第一个顶点

考虑线性规划的一般型：

这是一个含有 $n$个变量， $m$个约束的线性规划，我们可以先把它化成松弛型。

要解这个问题，我们的思路当然就是先找到这个多胞型里面的一个顶点，然后从这个顶点出发转移到其他顶点。

那么第一个顶点如何求呢？

可以使用下面的方法，构造一个辅助的线性规划，通过解这个辅助的线性规划得到一个顶点；如果找不到顶点，那么说明没有可行解。

这个辅助线性规划的意思是说，既然这m个约束都是小于等于的约束，那么现在我们往里面再添加一个松弛变量 $x_{0}$，使得：
$a_{11}x_{1} + a_{12}x2+\dots+a_{1n}x_{n}<=b_1 +x_{0}$
$a_{21}x_{1} + a_{22}x2+\dots+a_{2n}x_{n}<=b_2 +x_{0}$
$a_{m1}x_{1} + a_{m2}x2+\dots+a_{mn}x_{n}<=b_m +x_{0}$
而且依然保持任意的变量 包括松弛变量非负，即 $x_{i}>=0，i\in{0,1,2,3,4...,n}$

然后我们最小化 $x_{0}$，如果得到 $x_{0}$的最小值为0，那么说明原来所有小等于约束条件都是满足，如果 $x_{0}$大于0，比如说 $x_{0}$ 为1，那就说明原来这些条件都是没法满足的，意味着可行解为 $\empty$。

于是问题就转而求这个辅助线性规划了。观察一下这个辅助线性规划，它有很好的性质。

把它转为松弛型：

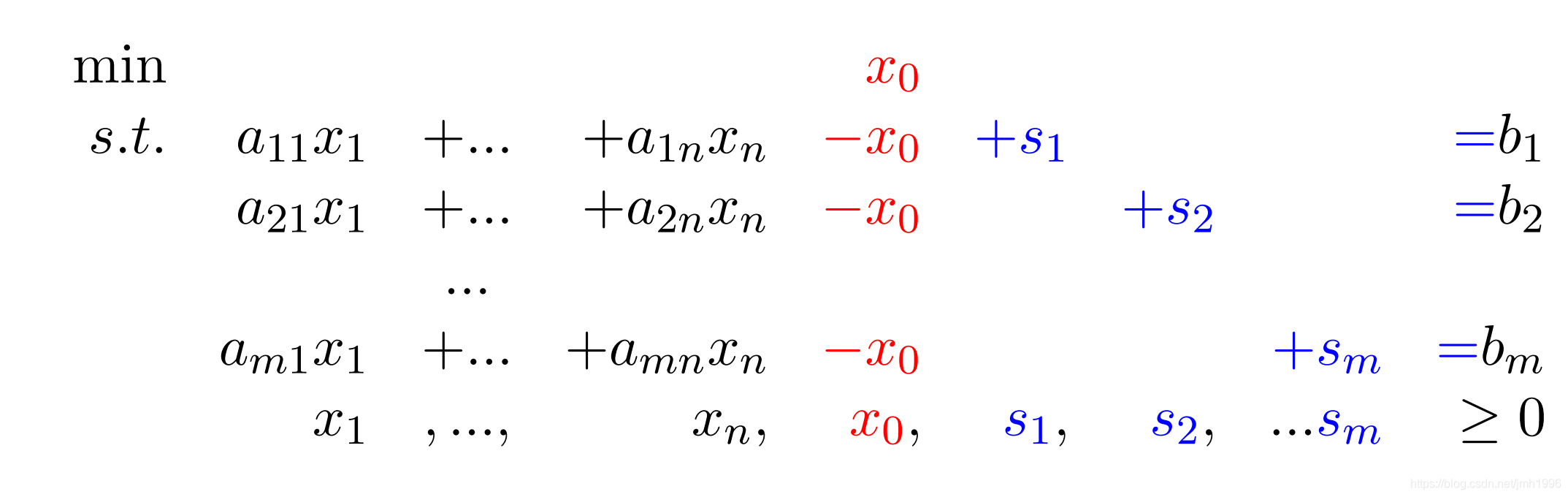
其中 $s_1,s_2,...,s_m$是m个松弛变量，他们都是非负的。而且这些松弛变量的前面的系数都是1，这是相当好的。

假设，任意的 $b_i>=0$的，其中 $i\in 1,2,3,...,m$,那么：让这些松弛变量就等于对应的 $b_i$ 就已经是解了。即 $s_i=b_i$。此时， $x_1=x_2=x_3=...=x_n=x_0=0$，而 $x_0$也等于0。

于是 $x_1=x_2=x_3=...=x_n=0$ 是原线性规划的一个顶点（注意这里有超过n-m个0）。此时，任选m列都是线性无关的，可以作为对应的基本列。

当存在 $b_i <0$ 的时候，这个时候就麻烦了，不可以直接 $s_i=b_i$了，因为这样会导致这种解（含义小于0的分量）不是辅助线性规划的解。

这个时候的做法，很简单，选中所有的 $b_i$里面 负的最厉害的那个（小于0，且最小的），假设负的最厉害的是 $b_j$。即 $b_j<0$,而且 $b_j\leq b_i,\space \forall \space i\in 1 ,2,3,...,m$。

让所有除 $b_j$的行都减去第j行（包括b那一列），这样，所有的 $b'_i=b_i-b_j>0$。然后把第j行同时乘以-1。这样就可以把所有的 $b'$ 都调整为非负。然后再在里面选中一组合适的基本列。

下一篇博客，我们就来面对单纯型法里面的一些特殊情况，例如：无界、死循环、以及实现的问题。