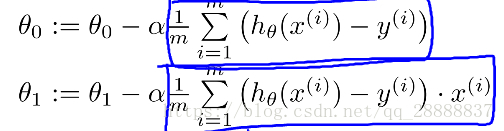python实现线性回归.md

python实现线性回归

一、相关数学推导

1.问题描述

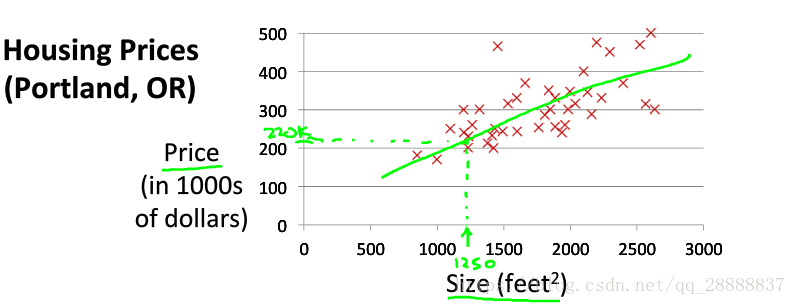
所谓线性回归，就是给你一批数据比如房子的面积以及房子的价格，然后你所做的就是找到一条线能尽量的拟合这一批数据。如下所示。

这里写图片描述

其中红色点就是给出的数据集合，有size代表面积，而price代表价格，红色点点就代表实际统计的数据，而线性回归的目的就在于找到那条最好的绿色直线，能使得这个绿色直线与所有红色点的差距最小。

2. 误差函数引出

上面可以看出我们要找到一条绿色的直线来拟合红色的点，在这里我假设这条绿色直线为： $h_\theta(x) = \theta_0 +\theta_1x$ ,这个函数也叫做假设函数，因为这条是我假设出来的，那么这个假设函数和真正的数据的距离可以使用欧式距离表示出来（当然你也可以使用其他的方式表示） $\frac{1}{2m} \sum_{i=1}^m （h_\theta(x^i) - y^i）$ ,这里计算的就是所有样本点的误差值，其中m代表所有红色点的个数，而 $x^i ,y^i$ 代表着第i个样本数，也就是第i个红色点的横坐标以及纵坐标，在有了上面的引入后，自然而然就得到了相应的误差函数为 $J(\theta_0,\theta_1) = \frac{1}{2m} \sum_{i=1}^m （h_\theta(x^i) - y^i）$ 其中 $h_\theta(x) = \theta_0 +\theta_1x$ ，所以我们现行回归的问题本质就是找到对应的 $\theta_0,\theta_1$ 使得 $J(\theta_0,\theta_1)$ 最小化。

3. 梯度下降法

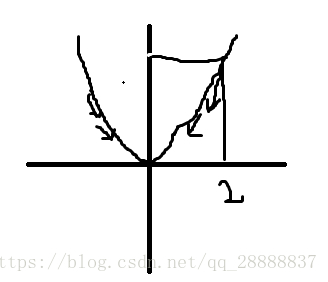
在求解最小化的过程中有一种方法叫做梯度下降法。让我们先看一下简单的梯度下降的过程，假如现在误差函数为 $J = \theta ^2$ ，假如目前我们 $\theta$ 的初始化为2，那么梯度下降的方式就是按照斜率（导数）的方向向下走，即 $\theta = \theta -\alpha \frac {dJ}{d\theta}$ ,其中 $\alpha$ 代表学习率，你可以看做每次减小是的步长，如果 $\alpha$ 比较大那么下降会快，小的话下降会慢，对于这个例子来说就是 $\theta = 2- \alpha *2*2$ ，如果我们取 $\alpha = 0.3$ 那么经过这个梯度下降后 $\theta$ 更新为0.8，而根据 $J = \theta ^2$ 的图像我们可以看出 $J$ 是在朝着最低点的方向走去。

在这里插入图片描述

4. 对我们的误差函数进行梯度下降

在有了2、3的结论下，我们就可以对我们的误差函数进行梯度下降了，这样通过多次的迭代我们就能找到相应的 $\theta_0 ,\theta_1$ 是的我们的误差函数最小。

这里写图片描述

所以剩下的事情就是求出来 $J(\theta_0,\theta_1)$ 对 $\theta_0,\theta_1$ 的导数，这里需要高等数学的知识，在这里直接给出结论。

在这里插入图片描述

蓝色框中的内容就是 $J(\theta_0,\theta_1)$ 对 $\theta_0,\theta_1$ 的偏导数，而前面 $\alpha$ 对应还是学习率。

5.问题矩阵化

其实在有了4的结论我们就可以直接编程了，但是由于更新 $\theta$ 的时候两个式子不同，并且里面还有累加，所以导致我们计算不方便，所以这里就把整个问题矩阵话，这样的话我们使用python编写程序就可以直接使用numpy进行矩阵操作，而不使用for循环，并且还可以通过小技巧是的两个更新只变成一个矩阵的更新。

在这里我们把所有的样本红色点的 $x$ 变成一个 $m*1$ 的向量 $X$ ，每一行代表相应红色点的size ，同样的把 $y$ 也变成一个 $m*1$ 的向量 $Y$ ，而把 $\theta_0 和 \theta_1$ 变成一个2*1的列向量 $\theta$ ，这样就发生一个有趣的事情，你会发现给 $X$ 左边进行扩充一列1，那么你用 $X *\theta$ 后得到一个 $m*1$ 的向量，这个向量的每一行其实就是 $\theta_0 + \theta_1 x$ 也就是我们上面所谓的假设函数，在这里我们通过矩阵你发现可以一次性计算出m个假设函数，并且通过矩阵化给 $X$ 扩充一列，就能消除 $\theta_0,\theta_1$ 的区别。这样的话4的梯度下降就能改写成如下格式：

$\theta = \theta - \alpha \frac{1}{m} X^T (X\theta-Y)$ 其中 $X$ 是扩展过1后的矩阵, $\theta$ 则是 $\theta_0,\theta_1$ 组成，其实这个式子就是4中的那个只是换了一种表达方式而已，你可以自己手动吧4中的式子展开,就是一个矩阵乘法。

二、python编制代码

1. 加载数据

# 产生数据
def load_data():
    # 样本个数
    sample_size = 50
    x = np.mat(np.random.rand(sample_size,1)*10)
    # y是数据标签 大概样子就是3.6x+(+-2)
    y = np.array([3.6*x[i] + random.uniform(-1,1) for i in  range(x.shape[0])])
    y=np.mat(y.reshape(sample_size,1))
    return x,y

# v2版本 这个产生的数据可以在x前面加上一列1，这样可以避免b
def load_data_v2():
    x,y = load_data()
    one = np.mat(np.ones((x.shape[0],1)))
    x_ = np.c_[one,x]
    return x_,y

第一个load_data就是产生的正常数据第二个load_data 主要目的就是给x扩充一列1.

2. 求导数

# 损失函数对w求偏导数
def derivative_w(x,y,w):
    m = x.shape[0]
    dw = x.T*(x*w-y)/m
    return dw

求导数只需要按照上面的公式进行就行了。

3.计算损失值

# 计算损失值  
def loss(x,y,w):
    y_i = x* w
    return np.sum((y-y_i).T*(y-y_i))/x.shape[0]

就是每次你得到一个模型，就计算一下其和真正数据的偏差有多少。

4. 迭代梯度下降预测模型

def L_Regression():
    # 每次喂入数据量
    batch_size = 30
    # 学习率
    learing_rate = 1e-3
    # 总共训练次数
    step = 50000
    
    itear = []
    loss_value = []
    x,y = load_data_v2()
    # w 就是模型的权重，这里随机初始化
    #w = np.random.rand(1,1)
    w = np.random.rand(2,1)
    # 每次喂入一批数据的开始和结束
    start = 0
    end = start + batch_size
    # 进行迭代更新w以及b的值
    for i in range (step):
        w = w- learing_rate*derivative_w(x[start:end],y[start:end],w)
        if (i+1) %1000 ==0:
            loss_v = loss(x[start:end],y[start:end],w)
            print("the step is %d th,the loss is %f"%(i,loss_v))
            itear+=[i]
            loss_value+=[loss_v]
        start = (start+batch_size)%x.shape[0]
        end = start + batch_size
    # y_i 是预测值
    y_i = x*w
    #进行绘图
    fig = plt.figure()
    ax1 = fig.add_subplot(121)
    ax1.scatter(x.getA()[:,1],y.getA(),color = "yellow")
    ax1.plot(x.getA()[:,1],y_i,color = "skyblue")
    ax2 = fig.add_subplot(122)
    ax2.plot(itear,loss_value,color = "gray")

其中多了一个batch_size 的东西，主要是每次不把所有数据喂入，而是训练一部分，这样减小内存消耗。

参考

吴恩达机器学习
 https://blog.csdn.net/qq_28888837/article/details/81258339