ml课程：线性回归、逻辑回归入门（含代码实现）

以下是我的学习笔记，以及总结，如有错误之处请不吝赐教。

本文主要介绍简单的线性回归、逻辑回归先关推倒，以及案例代码。

昨天做项目发现K-means都忘了，想想之前很多基础都忘了，于是决定重新开始学一遍ml的基础内容，顺便记录一下，也算是梳理自己的知识体系吧。

机器学习：目前包括有监督、无监督、强化学习三个大的方向，昨天说过了，就不详细展开。

几个基本概念：

数据集，样本（samples）、特征（features）、标签（labels）、输入空间、特征空间（feature vector），输出空间，如下图。

下面开始讲重点：线性回归和逻辑回归。

在说这两个初级算法之前，首先要知道算法包含的三个基本模块：目标函数、损失函数、优化算法。

线性回归：

简单说就是我们都学过的，线性方程:y=kx+b,输入一个x，得到一个y。

那么我们将它写成向量形式更好计算：

因此它的目标函数就是：

损失函数：是最简单的平方损失，即：预测点与实际点的差值平方/样本点个数。具体表示为：

其中： $\Theta$ 为权重， $_{h\Theta}$ 表示预测值，y表示实际值，m表示样本点个数，除以2是为了方便计算求导。

由于该损失函数为凸函数：

（二元情况）

（多元情况）

因此得到其优化函数为：梯度下降，即Gradient descent，沿梯度下降的方向逐渐减小其损失。为什么不直接对原方程求逆举证呢？因为第一计算资源有限，第二是因为有些矩阵并没有逆矩阵，因此我们用了这种启发式的函数。

函数形式如下：

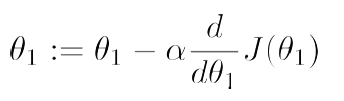
其中： $\alpha$ 表示学习率，即选择下降步子的大小，负号表示按照梯度下降方向。

（二元情况）

（多元情况）

这里还有一个正则化的问题：现实中我们处理的数据可能特征会很多，因此我们的模型可能会遇到以下两个问题：

欠拟合
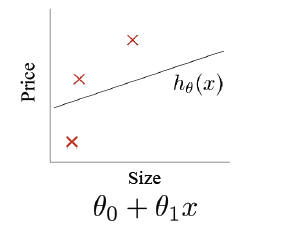
过拟合

一般情况下，我们遇到的都是过拟合现象，因为目前有很多高级的算法可以拟合出任何想要的曲线空间。所以我们加入正则化：

其中： $\lambda$ 表示正则化的权重，权重过小无法限制过拟合的情况，过大则会限制函数的拟合能力，下面代码阶段会举例说明。

线性回归实现核心代码：

# 计算损失函数
def computeCost(X, y, theta=[[0],[0]]):
    m = y.size
    J = 0
    
    h = X.dot(theta)
    
    J = 1.0/(2*m)*(np.sum(np.square(h-y)))
    
    return J

# 梯度下降
def gradientDescent(X, y, theta=[[0],[0]], alpha=0.01, num_iters=1500): #学习率设置为0.01
    m = y.size
    J_history = np.zeros(num_iters)
    
    for iter in np.arange(num_iters):
        h = X.dot(theta)
        theta = theta - alpha*(1.0/m)*(X.T.dot(h-y))
        J_history[iter] = computeCost(X, y, theta)  #返回损失函数
    return(theta, J_history)

具体代码可以看我之前码过得：python简单实现线性回归案例

逻辑回归：

逻辑回归名字及中是回归，其实是用来做分类，用来预测概率。

目标函数：sigmod函数， $g_{z}=\frac{1}{(1+e^{-z})}$ 。将y=kx+b阈值为（- $\infty$ ，+ $\infty$ ）映射到（0,1）之间的概率，因为sigmod函数拥有很好的数学特性， $g^{'}=g_{z}(1-g_{z})$ 。

损失函数：log损失函数，由于平方损失在sigmod上为非凸函数，且由于目标函数 $h_{\Theta }(x)$ 为一个p概率范围在（0,1）之间的数，我们想要得到p越大越好，就是-p越小越好，但是我们要对p求乘积时越来越小，因此我们加入log函数，使其变为加法，而且log函数为单调递增或递减的函数，不改变其单调性。具体函数如下：

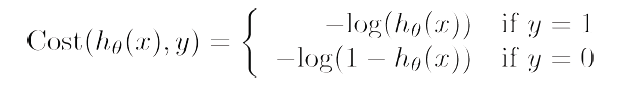
合并后：

加正则化项后：

$J(\theta) = \frac{1}{m}\sum_{i=1}^{m}\big[-y^{(i)}\, log\,( h_\theta\,(x^{(i)}))-(1-y^{(i)})\,log\,(1-h_\theta(x^{(i)}))\big]$$+\frac{\lambda }{2m}\sum_{i=1}^{m}\Theta _{j}^{2}$

向量化的公式：

$J(\theta) =- \frac{1}{m}\big((\,log\,(g(X\theta))^Ty+(\,log\,(1-g(X\theta))^T(1-y)\big) + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_{j}^{2}$

优化方法：依然还是梯度下降。

求偏倒：

$\frac{\delta J(\theta)}{\delta\theta_{j}} = \frac{1}{m}\sum_{i=1}^{m} ( h_\theta (x^{(i)})-y^{(i)})x^{(i)}_{j} + \frac{\lambda}{m}\theta_{j}$

向量化的偏导公式：

$\frac{\delta J(\theta)}{\delta\theta_{j}} = \frac{1}{m} X^T(g(X\theta)-y) + \frac{\lambda}{m}\theta_{j}$

核心代码：

#定义sigmod函数
def sigmod(z):
    return (1/(1+np.exp(-z))

#定义损失函数
def costFunction(theta, reg, *args):
    m = y.size
    h = sigmoid(X.dot(theta))
    
    J = -1.0*(1.0/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y)) +(reg/(2.0*m))*np.sum(np.square(theta[1:]))
               
    if np.isnan(J[0]):
        return(np.inf)  #np.inf表示无穷大的一个数
    return J[0]

#梯度下降
def gradinet(theta, reg, *args):
    m=y.size
    h=sigmod(X.dot(theta.reshape(-1,1)))
    grad = (1.0/m)*X.T.dot(h-y) + (reg/m)*np.r_[[[0]],theta[1:].reshape(-1,1)]
    return(grad.flatten())

应用：根据上面的学习，我们知道了算法的超参数，主要有：正则化系数、迭代轮次、学习率。因此我们在算法调优：

具体实现代码可以关注：我的github

未完，待续。