版权声明:本文为博主原创文章,若有错误之处望大家批评指正!转载需附上原文链接,谢谢! https://blog.csdn.net/summer_dew/article/details/84319196
二叉排序树
【二叉排序树】
- 二叉排序树可以是空树
- 结点p,它的左子树比它小,它的右子树比它大
【说明】
- 折半查找法的判定树就是一颗二叉排序树
- 对二叉排序树进行中序遍历,得到递增有序的序列
【基本操作】查找、插入、构建
typedef struct BTNode{
int key; //关键字
struct BTNode *lchild;
struct BTNOde *rchild;
}BiTNode, *BiTree;
// 查找的算法
BiTNode* BSTSearch(BiTree T, int key) {
if (T) {
if (T->key == key) return bt;
else if ( key< T->key ) return BSTSearch(T->lchild, key);
else return BSTSearch(T->rchild, key);
}
}
// 插入
int BSTInsert(BiTree *pT, int key) {
if ( (*pT)==NULL ) {
*pT = (BiTNode *)malloc(sizeof(BiTNode)); if ( !*pT ) exit(0);
(*pT)->key = key; (*pT)->lchild = (*pT)->rchild = NULL;
return 1;
} else {
if ( (*pT)->key == key ) return 0;
else if ( (*pT)->key > key ) return BSTInsert( &(*pT)->lchild, key);
else return BSTInsert( &(*pT)->rchild, key);
}
}
// 构建算法
void CreateBST(BiTree *pT, int key[], int n) {
int i;
*pT = NULL;
for (i=0; i<n; i++) BSTInsert(pT, key[i]);
}
【删除】二叉排序树有约束条件,删除时注意,需要分类讨论(这里选择的是更好理解的方法)
假设删除结点p,f是p的爸爸
- 【情况1】p为叶子结点:直接删除p
- 【情况2】p只有一个孩子:将p删除,用p的孩子替换p
- 【情况3】p有两个孩子
- 【第一步】p的关键字要删除,找一个结点r把p的位置顶上,结点r有两种找法
- 【第一种】去p的左子树上找:找p左子树上最大的结点(p往左走一步,再一直继续往右走,走到不能走,就找到了结点r)
- 【第二种】去p的右子树上找:找p右子树上最小的结点(p往右走一步,再一直继续往左走,走到不能走,就找到了结点r)
- 【第二步】把r的关键字替换掉p的关键字(完成了p的删除):
r->key = p->key - 【第三步】删除r结点(删除r的时候,肯定属于第1、2种情况的一种)
- 【第一步】p的关键字要删除,找一个结点r把p的位置顶上,结点r有两种找法
// 删除关键字key
int DeleteBST(BiTree *pT, int key) {
// 先查找到key,然后调用进行删除
if ( *pT ) {
if ( (*pT)->key == key ) return Delete(pT); //找到关键字
else if ( (*pT)->key > key ) return DeleteBST( &(*pT)->lchild, key);
else return DeleteBST( &(*pT)->rchild, key);
}
}
// 删除操作
int Delete(BiTree *pT) {
BiTNode *q, *r;
if ( (*pT)->lchild==NULL && (*pT)->rchild==NULL ) { //情况一
q = *pT;
*pT = NULL;
free(q);
} else if ( (*pT)->lchild && (*pT)->rchild ) { //情况三
r = (*pT)->lchild; //往左走一步
wihle (r->rchild) { //再往右走到尽头
r = r->rchild;
}
(*pT)->key = r->key; //r结点的key替换p,完成p关键字的删除
return Delete( &r ); //删除r结点:一定是情况一、情况二,不会出现循环调用
} else { //情况二
q = *pT;
*pT = (*pT)->lchild==NULL ? (*pT)->rchild : (*pT)->lchild; // 左子树为空 ? 挂上右子树 : 挂上左子树
free(q);
}
return TRUE;
}
平衡二叉树
| 名称 | 说明 | 图 |
|---|---|---|
| 二叉排序树 | 有时候会很低效(ASL=(1+2+3+4+5)/5=3,和没有建树一样) | 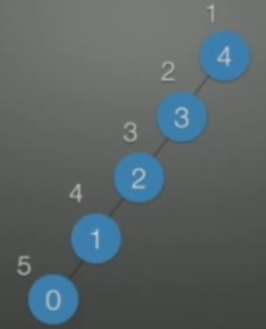 |
| 平衡二叉树 | 为了不让它这么长,边的扁一点矮一点胖一点,改进出了平衡二叉树(ASL=(1+2+2+3+3)/5=2.2) | 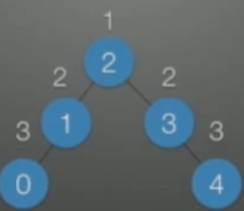 |
【约束条件】二叉排序树的进化,所有结点的左右子树高度之差的绝对值≤1
【平衡二叉树(AVL树)】一种特殊的二叉排序树,其左右子树都是平衡二叉树,且左右子树高度之差绝对值≤1
【定量判断】结点p,平衡因子=p左子树高度-p右子树高度,平衡因子的绝对值≤1
图中每个结点旁的数字代表该结点的平衡因子
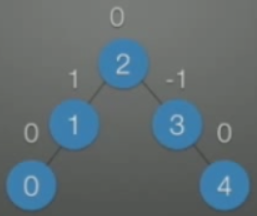
【平衡调整】|平衡因子|>1的结点即失去平衡,要进行平衡调整
【原理】
- 当失去平衡的最小子树被调整为平衡子树后,无需调整原有其他所有不平衡子树,整个二叉排序树就会变成一颗平衡二叉树
- 【失去平衡的最小子树】是以距离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树
【步骤】
- 插入新结点
- 插入后,找出失去平衡的最小子树
- 调整这棵子树,使之成为平衡子树
【调整的四种情况】LL型、RR型、LR型、RL型
| 名字 | 名字解释 | 说明 | 图例 |
|---|---|---|---|
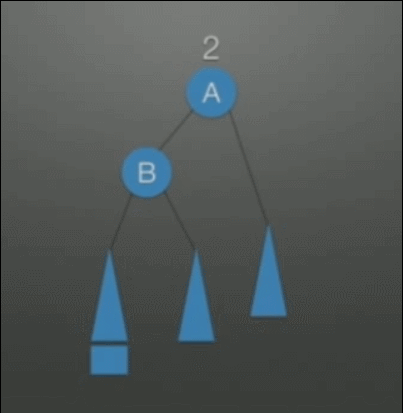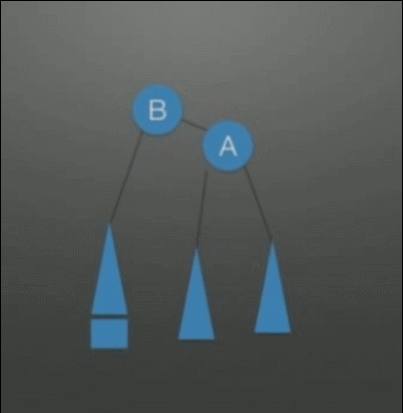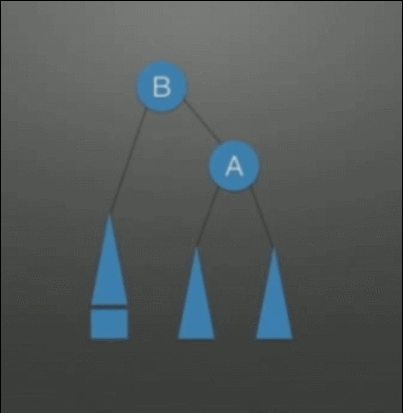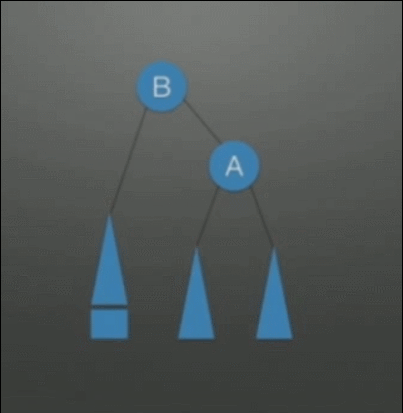
| LL(Left-Left)调整 右单旋转调整 |
在根(A)的左孩子(B)的左子树上插入结点,发生了不平衡 | 1. A往下旋转一个位置,变成B的右孩子结点 2. B的右子树挂在A的左子树上 |
 |
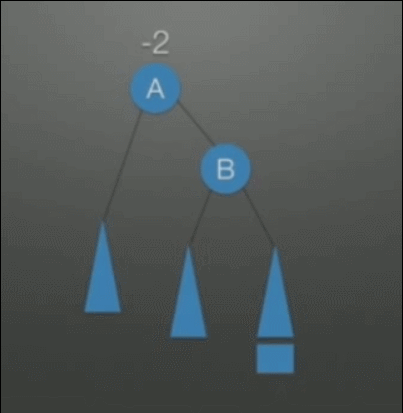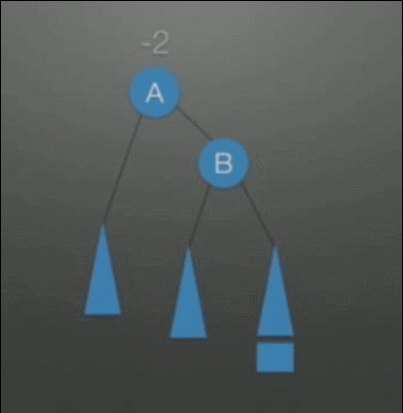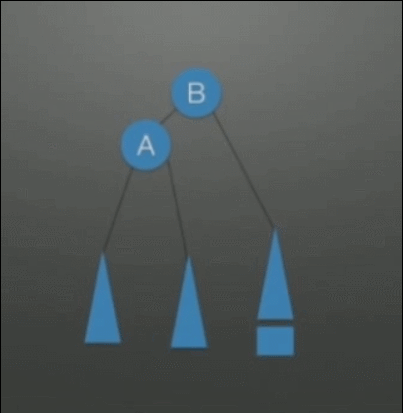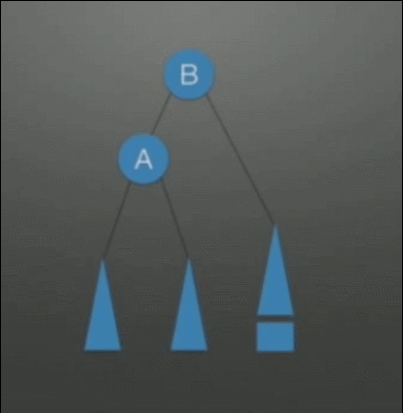
| RR(Right-Right)调整 左单旋转调整 |
在根(A)的右孩子(B)的右孩子上插入了结点,所发生的不平衡(是LL情况的对称情况) | 1. A往下旋转一个位置,变成B的左孩子 2. 将B的左孩子挂在A的右孩子上 |
 |
| LR调整 先左后右双旋转调整 |
在根结点(A)左孩子(B)的右子树上插入结点,导致不平衡 | 1. 把B整体摘下来,变成了RR的情况 2. 对B整体进行RR调整 3. 挂载A结点的空指针上,变成了LL的情况 4. 对A整体进行LL调整 |
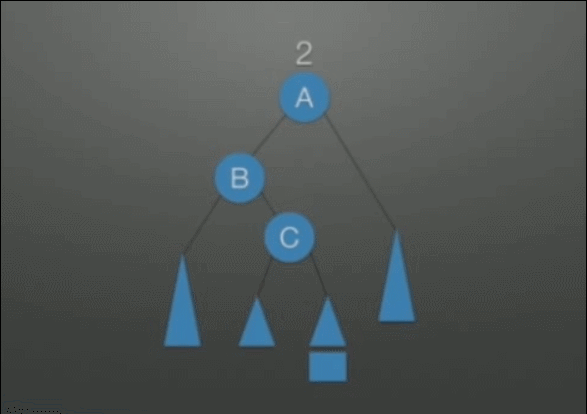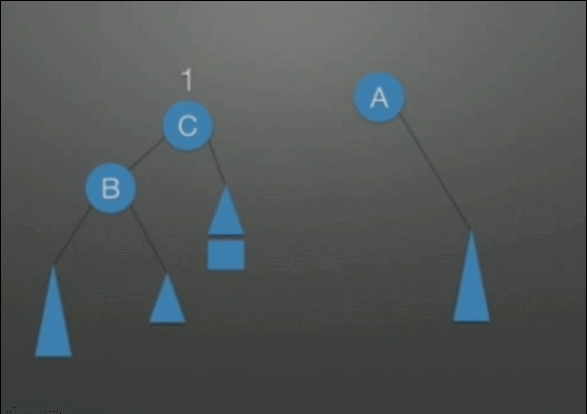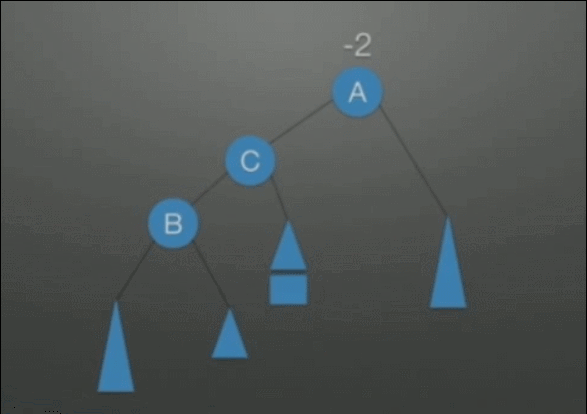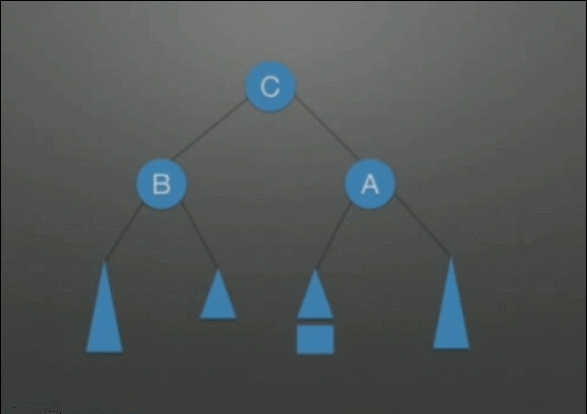 |
| RL调整 先右后左双旋转调整 |
根结点(A)的右孩子的左子树上插入结点,导致的不平衡(是LR调整的对称情况) | 1. 把B整体摘下来,变成了LL的情况 2. 对B整体进行LL调整 3. 挂在A结点的空指针上,变成了RR的情况 4. 对A进行RR调整 |
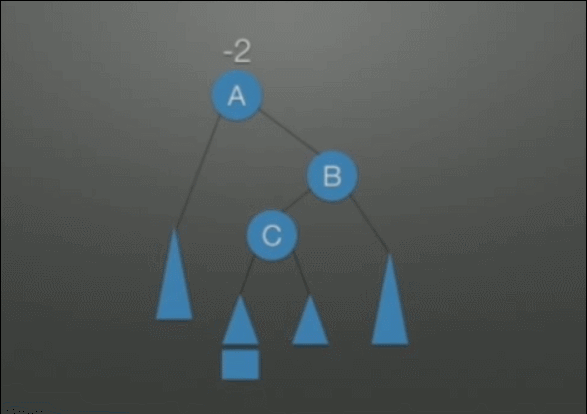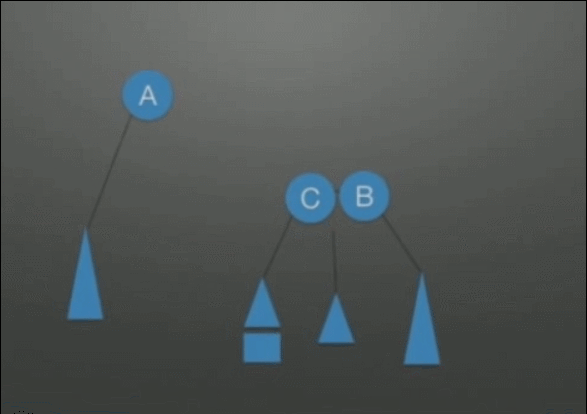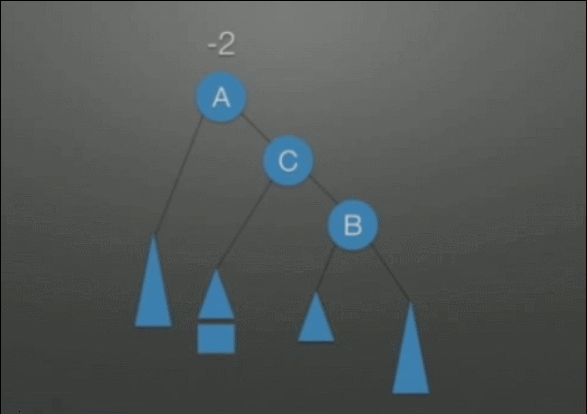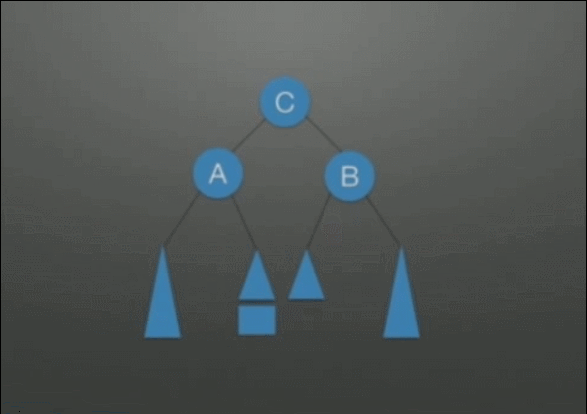 |
typedef struct BiTNode {
int data; //关键字
int bf; //平衡因子
struct BiTNode* lchild, *rchild;
}BiTNode, *BiTree;
#define LH +1 //左边高
#define EH 0 //左右高度相等
#define RH -1 //右边高
// 左单旋转调整(RR调整)
void L_Rotate(BiTree *A) {
BiTree B = (*A)->rchild; //得到B
B->bf = (*A)->bf = EH;
(*A)->rchild = B->lchild; //B的左子树给A的右子树
B->lchild = *A; //A挂到B的左子树上
*A = B;
return;
}
// 右单旋转调整(LL调整)
void R_Rotate(BiTree *A) {
BiTree B = (*A)->lchild;
B->bf = (*A)->bf = EH;
(*A)->lchild = B->rchild;
B->rchild = *A;
*A = B;
return;
}
// A的左子树变高了 - 有可能是LL、LR类型
void LeftBalance(BiTree* A) {
BiTree B = (*A)->lchild; //A的左子树
switch (B->bf) { //B的平衡因子
case LH: //B的左边更高 --> LL型
R_Rotate(A); //对A进行LL调整(即右单旋转调整)
break;
case RH: //B的右边高 --> LR型
L_Rotate(&B); //对B进行RR调整
(*A)->lchild = B; //挂在A的左子树上,代替刚才的B
R_Rotate(A); //A变成了LL情况,对A进行LL调整
break;
}
}
// A的右子树变高了 - 有可能是RL、RR类型
void RightBalance(BiTree *A) {
BiTree B = (*A)->rchild;
switch (B->bf) { //B的平衡因子
case LH: //B的左边更高 --> RL型
R_Rotate(&B); //对B进行LL调整(即右单旋转调整)
(*A)->rchild = B; //把新的根挂在A的空节点上
L_Rotate(A); //对A进行RR调整(即左单旋转调整)
case RH: //B的右边更高 --> RR型
L_Rotate(A); //对A进行RR调整(即左单旋转调整)
break;
}
}
// 平衡二叉树 - 插入结点
int InsertAVL(BiTree* pT,int data,int *taller) {
// @taller:该子树有没有变高,0未变高,1长高了
if( *pT == NULL ) { //找到插入位置
*pT = (BiTree)malloc(sizeof(BiTNode));
(*pT)->bf = EH; //左右高度相等
(*pT)->rchild = (*pT)->lchild = NULL;
(*pT)->data = data;
*taller = 1; //这棵子树长高了
return 1;
} else {
if ( data == (*pT)->data ) { //有相同的结点
*taller = 0;
return 0;
} else if ( data < (*pT)->data ) {
// 往左子树搜索
if ( InsertAVL( &(*pT)->lchild, data, taller) ) {
// 在左子树插入成功
if (*taller) {
// 左子树长高了
switch ( (*pT)->bf ) { //没插入前pT的平衡因子是
case LH: //没有插入前,pT左边就高出了1
LeftBalance(pT); //插入后左边不平衡-->调整
*taller = 0; //这棵没有变高,已经被处理掉了
break;
case EH: //没有插入前,pT两边平衡
(*pT)->bf = LH; //插入后,左边高出了1
*taller = 1; //这棵子树变高了
break;
case RH: //没有插入前,pT右边高
(*pT)->bf = EH; //插入后,左右平衡
*taller = 0; //这棵子树没有变高
break;
} //switch
} // if
return 1; //插入成功
} //if
} else if ( data > (*pT)->data ) {
// 往右子树搜索
if ( InsertAVL( &(*pT)->rchild, data, taller) ) {
// 在右子树插入成功
if (*taller) {
// 右子树长高了
switch ( (*pT)->bf ) { //没插入前pT的平衡因子是
case LH: //没插入前,pT的左子树高出了1
(*pT)->bf = EH; //插入后,左右平衡
*taller = 0; //这棵子树没有变高
break;
case EH: //没插入前,pT两边平衡
(*pT)->bf = RH; //插入后,右边高
*taller = 1; //这棵子树长高了
break;
case RH: //没插入前,pT的右子树更高
RightBalance(pT); //插入后,右子树不平衡
*taller = 0;
break;
} //switch
} //if
} //if
return 0;
} // else if
}
return 0; //插入失败
}