1 逻辑回归
1.1 概念
- 处理二分类问题
- 逻辑回归是广义的线性回归
- 将数据集带入Sigmoid分布函数,得到的结果大于0.5则判断为1,否则为0
1.2 推导方法
1.2.1 模型 - Sigmoid 分布函数
数据集:
zi=w0x0+w1x1+⋯+wixi=wTx(1)
zi 与线性回归模型很相似,一般情况下:
w0=b,
x0=1,也就是对应着线性函数中的截距项。
Sigmoid 分布函数:
f(zi)=1+e−zi1(2)
对每一个特征
x 乘上系数
w,然后通过 Sigmoid 函数计算
f(z) 值得到概率。其中,
z 可以被看作是分类边界,即将公式(1)代入公式(2)得到:
hw(x)=f(wTx)=1+ewTx1(3)
Sigmoid 函数图像:
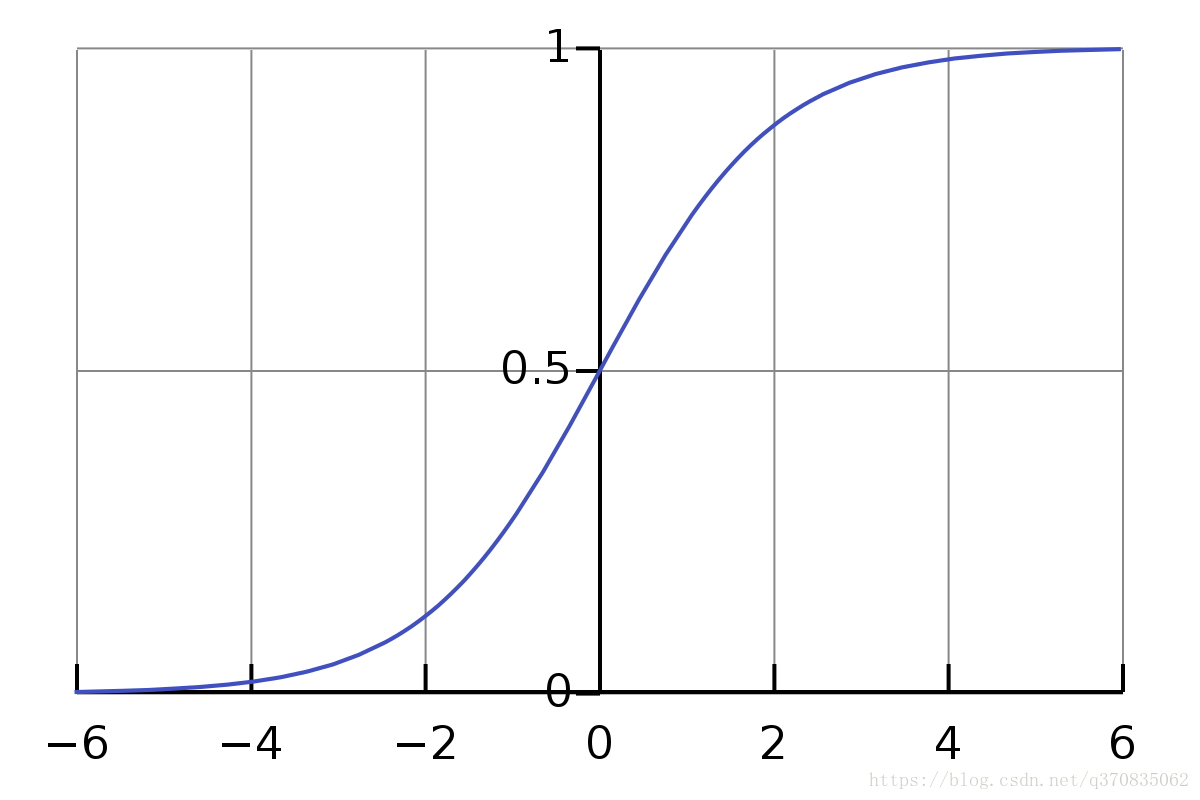
yi={01hw(x)<0.5hw(x)≥0.5(4)
1.2.2 目标函数 - 对数损失函数
J(w)=−m1i=1∑m[yilog(hw(xi))+(1−yi)log(1−hw(xi))](5)
目标就是求得 公式(5) 对数损失函数的 最小值
由于非凸函数,不能像最小二乘法求得全局最小值,所以需要用到梯度下降算法求解
1.2.3 求解方法
1.2.3.1 梯度下降法
针对公式(5)求导,得到梯度下降的方向
∂w∂J=m1XT(hw(x)−y)(5)
得到梯度的方向后,会定义一个 常数
α (学习率 Learning Rate),执行权重更新:
w←w−α∂w∂J(6)
如下图,每次更新
w0,
w1,
w2 … 直到获得最优解w*
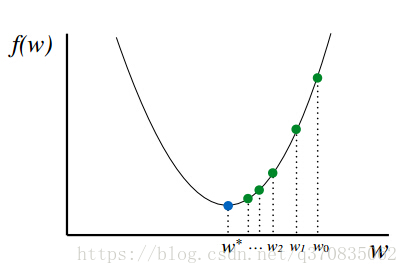
不断更新w的过程,即是:
w⟸w−αm1XT(hw(x)−y)(7)
1.2.4 性能度量
【 占位 - todo 】
2 Softmax
2.1 概念
2.2 推导方法
2.2.1 模型
数据集:
{(x1,y1),⋯,(xi,yi)}(8)
zi=wi0xi+wi1xi+⋯+wikxi=wkTxi(9)
其实
yi 这里是类别,有
{1,⋯,k}个类别,通过 Softmax函数 求得每个类别的概率:
p(yi)=∑i=1keziezi(10)
公式(9) 这里为什么是
wkTxi,这里演示一下
zi 的计算过程
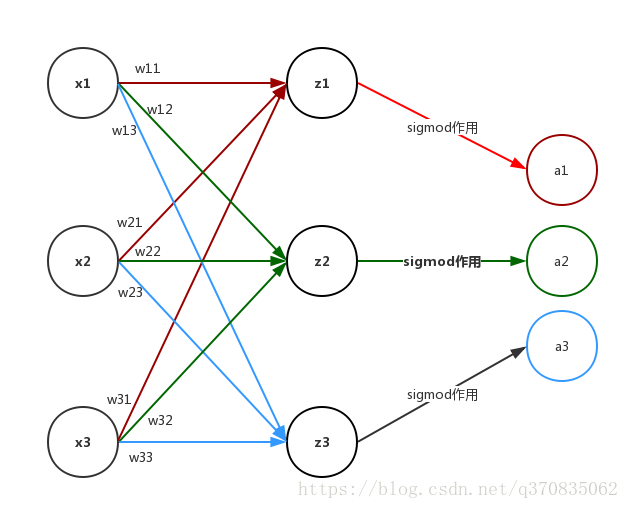
z1=w11x1+w21x2+w31x3z2=w12x1+w22x2+w33x3z3=w13x1+w23x2+w33x3
公式(10),
p(yi) 计算演示,注意:图中的
yi 应该是
p(yi)
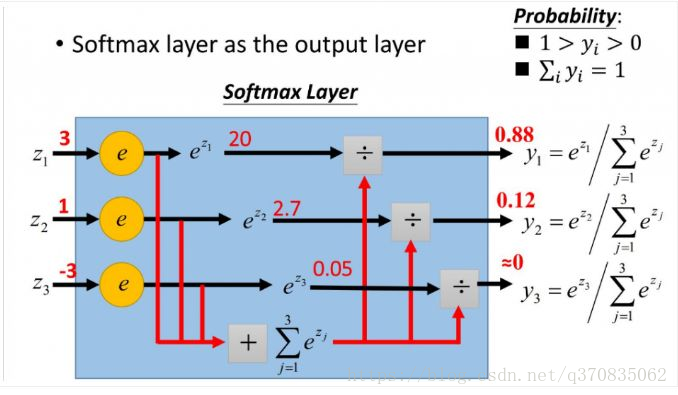
p(y1)=ez1+ez2+ez3ez1=e3+e1+e−3e3≈20+2.7+0.0520≈0.88p(y2)=ez1+ez2+ez3ez2=e3+e1+e−3e1≈20+2.7+0.052.7≈0.12p(y3)=ez1+ez2+ez3ez3=e3+e1+e−3e−3≈20+2.7+0.050.05≈0
∑p(yi)=p(y1)+p(y2)+p(y3)=0.88+0.12+0=1
看着计算过程,我们不难得到,我们的 模型函数:
hw(xi)=⎣⎢⎢⎡p(yi=1 ∣ xi ; θ)p(yi=2 ∣ xi ; θ)⋯p(yi=k ∣ xi ; θ)⎦⎥⎥⎤=∑l=1keθlTxi1⎣⎢⎢⎡eθ1Txieθ2Txi⋯eθkTxi⎦⎥⎥⎤(11)
2.2.2 目标函数 - loss函数
J(θ)=−m1[i=1∑mj=1∑k1{yi=j} log∑l=1keθlTxieθjTxi]=−m1[i=1∑m(1−yi)log(1−hθ(xi))+yilog(hθ(xi))]=−m1[i=1∑mj=1∑k1{yi=j} p(yi=j ∣ xi ; θ)](12)
公式(12)中的
1{yi=j} 是一个指示性函数,即当大括号中的值为真时(即
yi=j ),结果为1,否则为0
2.2.3 求解方法
2.2.3.1 梯度下降法
推导过程 可以参考 Softmax回归
这里不详细解释,过程可以参考 1.2.3.1 梯度下降法 理解
2.2.4 性能度量
【 占位 - todo 】
3 sklearn
3.1 逻辑回归
3.1.1 例子
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(tol=0.001, max_iter=10000)
model.fit(x, y)
model.coef_, model.intercept_
3.1.2 参数说明
模型参数详解 Google的文档
3.2 Sofrmax回归
3.2.1 例子
【 占位 - todo 】
3.2.2 参数说明
【 占位 - todo 】
4 优缺点
【 占位 - todo 】
5 算法对比
5.1 逻辑回归 vs 线性回归
5.2 逻辑回归/Softmax回归 vs 神经网络
6 疑问
- 逻辑回归的对数损失函数为什么是凸函数,要用梯度下降算法??
可以参考这两篇文章
机器学习总结之逻辑回归Logistic Regression
Proofs you probably weren’t taught
- 逻辑回归和Softmax回归除了梯度下降的方法,还有没有其他的求解方法?
参考资料
逻辑回归
第三章_线性模型:对数几率回归
逻辑回归算法面经
详解softmax函数以及相关求导过程
softmax 损失函数以及梯度推导计算
简单易懂的softmax交叉熵损失函数求导
Softmax回归
Logistic and Softmax Regression (逻辑回归和Softmax回归)



