一、前言
LCS是Longest Common Subsequence的缩写,即最长公共子序列。一个序列,如果是两个或多个已知序列的子序列,且是所有子序列中最长的,则为最长公共子序列。
另外还有个分支问题:最长公共子串。子串的字符位置必须连续,而子序列则不必,从原序列中去掉任意的元素获得的新序列。可以看出,子串问题比子序列问题要简单地多,子串必定是子序列,换言之,子串是子序列的子集。如果我们能解决子序列问题,子串问题也迎刃而解。
二、解法
2.1穷举法
穷举法是显而易见第一时间从脑子里蹦出来的想法,实际上代码层面的实现也不困难。提取出A序列的每一个子序列,检查其是否也是B序列的子序列,全部比对完后,比较出最长的一个子序列。
不考虑子序列重复的前提下啊,一个长度为n的序列,其子序列个数为2^n(容易理解,每一项取或不取)。易知其时间复杂度为O(2^n),指数级复杂度一般来说是不可接受的。
这里的空间复杂度我看一些文章说也是O(2^n),但是我觉得并不需要存下每一个子序列,每一个A的子序列经验证不是B的子序列后即可丢弃,所以存储的花费并不是所有子序列,而是所有公共子序列。所以我认为空间复杂度没有达到O(2^n),可能是我的理解有问题,如果有懂得观众看到这里,恳请指点一二。
2.2动态规划
记X = [x1,x2,...,xm]和Y = [y1,y2,...,yn]的一个最长公共子序列Z = [z1,z2,...,zk],则有:
1. 若xm=yn,则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列;
2. 若xm≠yn且zk≠xm,则Z是Xm-1和Y的最长公共子序列;
3. 若xm≠yn且zk≠yn,则Z是X和Yn-1的最长公共子序列。
其中Xm-1 = [x1, x2, …, xm-1],Yn-1 = [y1, y2, …, yn-1],Zk-1 = [z1, z2, …, zk-1]。
第2点和第3点可以合并为,max(LCS(Xm-1,Yn),LCS(Xm,Yn-1))。
2.3矩阵思想解题
记一个二维数组C[],c[i,j]存储Xi和Yi的最长公共子序列的长度。所以c[m,n]即矩阵最右下角的值为X与Y的最长公共子序列的长度。
虽然我们在递推过程是从序列的尾部开始的,但实际解题是从头部开始的,因为在计算max(LCS(Xm-1,Yn),LCS(Xm,Yn-1))时,需要事先计算出LCS(Xm-1,Yn)和LCS(Xm,Yn-1),才能比较他们的大小。
1. 先令c[i,0]整一列的值为0,显然任意序列与空序列的最长公共子序列长度为0;同理,令c[0,j]整一行的值为0;
2. 如果当前比较的两个字符xi=yj,令这个格子的c[i,j] = 1。方向为左上角(LeftTop);
3. 如果当前比较的两个字符xi≠yj,比较c[i-1,j]和c[i,j-1]的值,取其中较大的值填充入c[i,j]中,方向为值的来源方向左(Left)或者上(Top);
4. 一直迭代运算至二维数组C[]所有格子均有值,结束。
便于理解抄自网络的图:
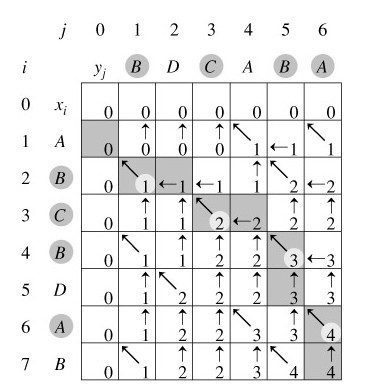
2.4小结
记录方向是为了构造出最长公共子序列,当然这样的算法有一个局限就是当LCS(Xm-1,Yn) = LCS(Xm,Yn-1)时会出现多解,即最长公共子序列不唯一。这样的情况显然是可预见的,所以在当出现LCS(Xm-1,Yn) = LCS(Xm,Yn-1)时两个方向都得记录,才能恢复出所有的最长公共子序列(如果有需要)。
当然,如果只是为了求得最长公共子序列的长度,方向是不必记录的。连矩阵都可以不用构造,因为c[i,j]的值完全来源于上一行的值,即c[i-1,j-1]、c[i-1,j]、c[i,j-1]三者其中之一,只需要记录矩阵中的两行数据即可,空间复杂度进一步降低。
2.5子问题1——最长公共子串
解决了最长公共子序列问题,最长公共子串就简单地多了。仍然是构造二维矩阵C[],当xi = yj时,令c[i,j] = c[i-1,j-1],然后矩阵中最大的元素就是最长公共子串的长度。构造最长公共子串也只需要找出最长的一条斜对角线即可。
附Python实现:
def find_lcs_len(input_x, input_y):
dp = [([0] * len(input_y)) for i in range(len(input_x))]
maxlen = 0
for i in range(0, len(input_x)):
for j in range(0, len(input_y)):
if input_x[i] == input_y[j]:
if i != 0 and j != 0:
dp[i][j] = dp[i - 1][j - 1] + 1
if i == 0 or j == 0:
dp[i][j] = 1
if dp[i][j] > maxlen:
maxlen = dp[i][j]
return maxlen2.6子问题2——最长递增子序列(LIS)
看到这有些人可能会疑惑,最长递增子序列只关系到一个序列。如序列X = [5,8,2,3,9,4,7]的LIS为[2,3,4,7]。而LCS问题是两个序列的公共子序列问题。
其实这里先构造一个辅助序列X' = [2,3,4,5,7,8,9],即对X排序生成的新序列。对序列X和X’求LCS就是这个问题的解。这里不再详细论述,相信聪明的读者都容易看懂其中逻辑。
三、总结
用LCS算法代替穷举法来解决最长公共子序列问题,时间复杂度由O(2^n)下降到了O(n*m),空间复杂度也是同等级数的下降。经由精妙的LCS算法,为我们方便地解决了运算起来繁复的问题。
有机会得继续学习这些有趣奇妙的算法。另外,我也得花时间去理解下复杂度的计算,之前一直是我的盲点。
收!