上一节我们详细的探讨了玻尔兹曼机，玻尔兹曼机的发明是为了解决Hopfield神经网络的伪吸引子的问题，因此把退火算法、玻尔兹曼分布和Hopfield神经网络结合在一起形成了玻尔兹曼机（随机神经网络）。通过前面几节我们知道玻尔兹曼机可以很好的解决Hopfield神经网络的伪吸引子的问题，但是带来的另外一个大问题就是计算量太大了，训练周期长，因此Hinton和Sejnowski于1986年提出的一种生成式随机神经网络(generative stochastic neuralnetwork)即受限玻尔兹曼机，其实受限玻尔兹曼机是在玻尔兹曼机的基础上通过Gibbs采样，进而提升了计算速度，也因此受限玻尔兹曼机得到广泛应用，但是想要搞明白Gibbs采样不是一件容易的事，他需要很深的背景知识，想要理解Gibbs采样就需要理解MCMC和Metropolis算法，想要理解MCMC就需要理解马尔科夫链，想要理解马尔科夫链就需要理解马尔科夫过程，因此这里需要很深的背景知识，我打算从最初的马尔科夫过程继续深入讲解，因为这些知识不仅仅这里使用到，在强化学习、自然语言处理都是经常使用的，搞明白他们很有必要，尤其马尔科夫过程，整个强化学习就是基于马尔科夫为基础的，因此深入理解他很有必要，而隐马尔可夫又是自然语言处理经常使用的，因此深入理解他们很有必要，从这里也可以看出，知识点并不是孤立的，他们都是有联系的，讲的简单点就是方法论，他们都是相通，因此大家学习时就要学会举一反三，触类旁通，然而想达到这样的地步，你必须深入理解他们。好了，废话不多说，大家都知道了问题和学习过程，下面我们就按照上面的过程进行逐步讲解。
在讲解马尔科夫过程之前呢，先和大家简单介绍一下随机过程，这里如果不懂随机过程的同学，建议看一下浙大的《概率统论与数理统计》这本书第12章和13章的内容，因为马尔科夫过程就会根据这本书进行介绍，因此想要深入理解的请看这本书，当然我会尽量讲清楚的。
随机过程：
具体的例子请参考《概率统论与数理统计》第四版301页，我只把定义拿过来，不懂随机过程的建议看看。
连续型随机过程：
设T是一无限实数集，我们把依赖于参数的一族（无限多个）随机变量称为随机过程，记为
，这里对每一个
，
是一随机变量，T叫做参数集．我们常把t看作为时间，称
为时刻t时过程的状态，而
(实数）说成是
时过程处于状态x，对于一切
，
所有可能取的一切值的全体称为随机过程的状态空间．
对随机过程进行一次试验（即在T上进行一次全程观测），其结果是t的函数，记为
，
称它为随机过程的一个样本函数或样本曲线，所有不同的试验结果构成一族样本函数．随机过程可以看作是多维随机变量的延伸．随机过程与其样本函数的关系就像数理统计中总体与样本的关系一样．
离散型随机过程：
随机过程还可依时间（参数）是连续或离散进行分类．当时间集T是有限或无限区间时，称为连续参数随机过程（以下如无特别指明，“随机过程”总是指连续参数而言的).如果T是离散集合，例如T={0，1，2，．．}，则称
为离散参数随机过程或随机序列，此时常记成
等
这是基本的随机过程的定义，但是我们知道随机过程如果不加以限制，则无法研究，为了研究方便，加入一些限制，例如平稳随机过程、马尔科夫随机过程，这里简单的介绍一下平稳随机过程，详细介绍马尔科夫随机过程。
平稳随机过程定义;
过程的统计特性不随时间的推移而变化，严格的说，如果对于任意的和任意实数h，当
时，n维随机变量：
和
具有相同的分布函数，则称随机过程具有平稳性，并同时称此过程为平稳随机过程，或简称平稳过程。
马尔科夫过程定义：
由时刻系统或过程所处的状态，可以决定系统或过程在时刻
所处的状态，而无需借助于
时刻以前的转态，简单来说就是将来不依赖过去只依赖现在。举个例子吧，书中讲的太生硬了，例如明天下不下雨只和今天有关，和昨天、前天无关说明天气就具有马尔科夫性或者无后效性 （即已经知道过程‘现在’的条件下，其“将来”不依赖于“过去”）。我们就称具有马尔科夫性的随机过程称为马尔科夫过程。具体的书面定义如下：
如果时间和状态都是离散的我们称为马尔科夫链简称为马氏链。下面给出例子：
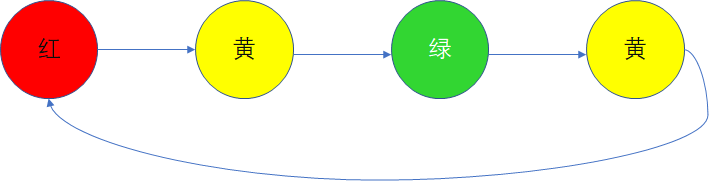
交通灯的就具有马尔科夫性，红到黄转移概率为1，黄到绿转移概率也是1，但是红到绿转移G概率为零，即下一个转向概率只和本次灯有关。在举个例子
这个是昨天天气转移到今天天气的方向图，但是这个图看转移概率很麻烦，因此我们可以使用转移矩阵来表示：
从上面的转移概率矩阵我们可以看到，今天的天气只取决于昨天，使用矩阵来表示很清晰间接，这个矩阵怎么看呢？第一行表示昨天是晴天那么转移到今天为晴天的概率为0.5，转移到今天是多云的概率是0.375，转移到雨天的概率为0.125，在这里只有三种天气，因此，每行的概率和为1，又因为昨天的天气也有三种情况，概率也为1，因此这转移概率矩阵每行每列的概率和均为1，这就是概率转移矩阵，下面给出书面对这方面的介绍：
这里大家好好理解转移概率的平稳性，只与ij和时间距离有关系，按照上面的例子，ij其实就是昨天和今天，而时间距离就是1，如果时间距离是n=2，说明昨天影响的是后天，那前前天影响的才是今天，这里大家需要多注意，多理解一下。需要搞明白n步转移概率和一步转移概率是什么意思，我们上面举得例子就是一步的，因为时间单位是1天，因此昨天影响今天就是一天的间隔，如果前天影响今天，昨天影响明天，这里的时间间隔就是n=2,即两天时间，这里大家需要好好理解，建议看看上面推荐的书。下面给出一步转移概率相关信息：
大家理解时完全可以按照天气来理解，上图的矩阵代表昨天，而昨天的天气具体有三个状态即晴天、多云、雨天；
代表的是今天，然而今天也有三个状态即晴天、多云、雨天，这里的该变量是
即昨天或者今天、明天等，但是每天的天气的状态的个数是一样的，这里容易搞混的，所有我强调一下。因此每天的天气状态是固定的，因此转移矩阵一定是方阵，这里大家一定要理解，否则后面就会很困难了。另外需要强调一下就是一步转移概率的表示即
，这个很重要，只要掌握了一步转移概率，那么多步的就容易理解了，因为多步的可以通过一步的来推到出来。大家这段需要好好理解一下。
多步转移概率的确定：
下面我们就看看多步转移概率矩阵，这里大家请去看看《概率统论与数理统计》第四版325页的多步转移概率的确定，这里我直接把结果拿过来了：
矩阵形式的方程有这个性质：
具体证明请查看书本。
那么根据ck方程我们很容易通过一步转移概率矩阵求多步转移概率矩阵：
令,代入上式得:
简单来说就是对于其次马氏链来说，n步转移概率矩阵就是一步转移概率矩阵的n次方。
有这个等式就简单了，如果需要求n转移概率矩阵，我们只需要求出一步转移概率矩阵，然后n次方一步转移概率矩阵就可以了，这里就考验大家的矩阵基础了，这里举个例子如何求矩阵的m次方的例子(在科学计算包只需一个函数接口就可以完成计算，很简单)：
遍历性：
《概率统论与数理统计》第四版328页
这里我先简单的说明一下，然后在给出书面定义，这里大家需要理解是什么意思，根据
可以知道，根据我们前面的举例，天气，ij其实代表的就是昨天和今天的意思，这里大家需要注意，详情请查看书本。下面介绍遍历性，所谓遍历性，就是说无论我从什么状态开始，经历多次转移以后，最后都会到达一个状态，那么满足这样的马尔科夫性性就称为具有遍历性，下面给出书面的定义：
例子
我们先来看马氏链的一个具体的例子。社会学家经常把人按其经济状况分成3类：下层(lower-class)、中层(middle-class)、上层(upper-class)，我们用1，2，3分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别，那么他的孩子属于下层收入的概率是0.65，属于中层收入的概率是0.28，属于上层收入的概率是007。事实上，从父代到子代，收入阶层的变化的转移概率如下
使用矩阵来表示，即概率的转移矩阵为：
假设当前这一代人处在下层、中层、上层的人的比例是概率分布向量，那么他们的子女的分布比例将是
，他们的孙子代的分布比例将是
，，第n代子孙的收入分布比例将是
。
假设初始概率分布为，则我们可以计算前n代人的分布状况如下:
我们发现从第7代人开始，这个分布就稳定不变了，这个是偶然的吗？我们换一个初始概率分布试试看，继续计算前n代人的分布状况 如下：
我们发现，到第9代人的时候，分布又收敛了。最为奇特的是，两次给定不同的初始概率分布，最终都收敛到概率分布，也就是说收敛的行为和初始概率分布
无关。这说明这个收敛行为主要是由概率转移矩
阵决定的。我们计算一下
:
我们发现，当n足够大的时候，这个矩阵的每一行都是稳定地收敛到
这个概率分布。自然的，这个收敛现象并非是我们这个马氏链独有的，而是绝大多数马氏链的共同行为，关于马氏链的收敛我们有如下漂亮的定理：
大家通过这个例子应该可以理解平稳性 即遍历性，希望大家可以深入理解马尔科夫链，因为下几节会使用到，本节到此结束。
注：例子来源《LDA数学八卦》