1.背景知识:
1.1随机过程:就是一些统计模型,利用这些统计模型可以对自然界的一些事物进行预测和处理,比如天气预报,比如股票,比如市场分析,比如人工智能。它其实就是个过程,比如今天下雨,那么明天下不下雨呢?后天下不下雨呢?从今天下雨到明天不下雨再到后天下雨,这就是个过程。那么怎么预测N天后到底下不下雨呢?这其实是可以利用公式进行计算的,随机过程就是这样一个工具,把整个过程进行量化处理,用公式就可以推导出来N天后的天气状况,下雨的概率是多少,不下雨的概率是多少。
1.2 马尔可夫性质
马尔可夫性质是概率论中的一个概念:当一个随机过程在给定现在状态及所有过去状态的情况下,其未来状态的条件概率分布仅依赖于当前状态。
简而言之,随即过程中某状态的发生只取決它上一个时刻的状态,那么此随机过程即具有马尔可夫性质。数学上,如果X(t),t>0为一个随机过程,则马尔可夫性质的定义如下:
Pr[X(t+h)=y|X(s)=x(s),s⩽t]=Pr[X(t+h)=y|X(t)=x(t)],∀h>0
一般来说,具备马尔可夫性质的随机过程是不具备记忆特质的。在这个系统中,现在的条件概率和过去及未来的状态都是独立且不相关的,具备马尔可夫性质的过程通常称为马尔可夫过程
1.3马尔科夫过程:
就是指过程中的每个状态的转移只依赖于之前的 n个状态,这个过程被称为 n阶马尔科夫模型,其中 n是影响转移状态的数目。最简单的马尔科夫过程就是一阶过程,每一个状态的转移只依赖于其之前的那一个状态,这也是后面很多模型的讨论基础,很多时候马尔科夫链、隐马尔可夫模型都是只讨论一阶模型,甚至很多文章就将一阶模型称之为马尔科夫模型,现在我们知道一阶只是一种特例而已了。
总结:马尔科夫过程指的是一个状态不断演变的过程,对其进行建模后称之为马尔科夫模型,在一定程度上,马尔科夫过程和马尔科夫链可以打等号的。
1.4马尔可夫链:
俄国数学家 Andrey Andreyevich Markov 研究并提出一个用数学方法就能解释自然变化的一般规律模型,被命名为马尔科夫链(Markov Chain)。
时间和状态都是离散的马尔可夫过程称为马尔可夫链,简记为Xn=X(n),n=0,1,2…马尔可夫链是随机变量X1,X2,X3…的一个数列。
马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程,该过程要求具备“无后效性 ”,所谓的无后效性,即对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,即下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。
马尔科夫链认为过去所有的信息都被保存在了现在的状态下了 。比如这样一串数列 1 2 3 4 5 6,在马尔科夫链看来,6 的状态只与 5 有关,与前面的其它过程无关。
数学定义:
对于一阶马尔科夫模型,则有
则假设我们的序列状态是. . . . X t − 2 , X t − 1 , X t , X t + 1 . . . ....
那么在X t + 1 时刻的状态的条件概率仅依赖于前一刻的状态X t
即: P(Xt+1∣…Xt−2,Xt−1,Xt)=P(Xt+1∣Xt)
2.马尔科夫模型
首先了解什么是转移概率矩阵
通过马尔科夫链的模型转换,我们可以将事件的状态转换成概率矩阵 (又称状态分布矩阵 ),如下例:
上图中有 A 和 B 两个状态,A 到 A 的概率是 0.3,A 到 B 的概率是 0.7;B 到 B 的概率是 0.1,B 到 A 的概率是 0.9。
初始状态在 A,如果我们求 2 次运动后状态还在 A 的概率是多少?
P = A → A → A + A → B → A = 0.3 ∗ 0.3 + 0.7 ∗ 0.9 = 0.72 P = A→A→A + A→B→A = 0.3 * 0.3 + 0.7 * 0.9 = 0.72P=A→A→A+A→B→A=0.3∗0.3+0.7∗0.9=0.72
如果求 2 次运动后的状态概率分别是多少?初始状态和终止状态未知时怎么办呢?这是就要引入转移概率矩阵 ,可以非常直观的描述所有的概率。

有了状态矩阵,我们可以轻松得出以下结论:
初始状态 A,2 次运动后状态为 A 的概率是 0.72;
初始状态 A,2 次运动后状态为 B 的概率是 0.28;
初始状态 B,2 次运动后状态为 A 的概率是 0.36;
初始状态 B,2 次运动后状态为 B 的概率是 0.64;
有了概率矩阵,即便求运动 n 次后的各种概率,也能非常方便求出。
状态转移矩阵的稳定性
状态转移矩阵有一个非常重要的特性,经过一定有限次数序列的转换,最终一定可以得到一个稳定的概率分布 ,且与初始状态概率分布无关。
接下来举一个马尔科夫的实例:
马尔科夫模型的案例——天气预报
下面是一个马尔科夫模型在天气预测方面的简单例子。如果第一天是雨天,第二天还是雨天的概率是0.8,是晴天的概率是0.2;如果第一天是晴天,第二天还是晴天的概率是0.6,是雨天的概率是0.4。问:如果第一天下雨了,第二天仍然是雨天的概率是多少?,第十天是晴天的概率是多少?;经过很长一段时间后雨天、晴天的概率分别是多少?
首先构建转移概率矩阵,由于这里每一天的状态就是晴天或者是下雨两种情况,所以矩阵是2x2的,如下:

注意:每列和为1,分别对雨天、晴天,这样构建出来的就是转移概率矩阵了。如下:
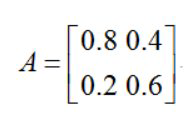
假设初始状态第一天是雨天,我们记为
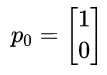
这里【1,0】分别对于雨天,晴天。
初始条件:第一天是雨天,第二天仍然是雨天(记为P1)的概率为:
P1 = AxP0
得到P1 = 【0.8,0.2】,正好满足雨天~雨天概率为0.8,当然这根据所给条件就是这样。
下面计算第十天(记为P9)是晴天概率: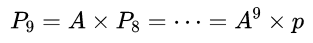
得到,第十天为雨天概率为0.6668,为晴天的概率为0.3332。
下面计算经过很长一段时间后雨天、晴天的概率,显然就是下面的递推公式了:
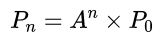
当n趋于无穷即很长一段时间以后,Pn = 【0.67,0.33】。即雨天概率为0.67,晴天概率为0.33。并且,我们发现:初始状态如果是P0 =【0,1】,最后结果仍然是Pn = 【0.67,0.33】。这表明,马尔科夫过程与初始状态无关,跟转移矩阵有关。