本文分为两大部分即PCA和SVD，每一部分下又分为原理和应用两小部分

说明：本文代码参考Peter Harrington编写的Machine Learning in Action,感兴趣的小伙伴可以去看一下，笔者认为这本书还不错

注意：本篇重在说明公式推导，关于具体使用的话python有专门的机器学习库已经集成，直接用就可以啦，可以在读完本文的理论部分后再去看笔者另一篇应用了PCA的关于人脸识别的一个简单例子https://blog.csdn.net/weixin_42001089/article/details/79989788

废话不多说开始吧

PCA:

（1）原理

$(1)XV=\lambda V$

$(2)XV=V\Sigma \Rightarrow X=V\Sigma V^{-1}=V\Sigma V^{T}$

公式（1）是我们熟悉的求特征值的式子，假设X是m*m，我们根据其求出了 $\lambda _{1},\lambda _{2},\cdots \lambda _{m}$ 特征值以及每个特征值对应的特征向量。

---------------------------------------------------------------------------------------------------------------------------------------------------------------

关于怎么求特征值这里简单举一个小例子：会的话直接跳过就可以啦

$X=\begin{pmatrix} 2 & 1\\ 1& 2 \end{pmatrix}$

$\begin{vmatrix} 2-\lambda &1 \\1 & 2-\lambda \end{vmatrix}=(2-\lambda )^{2}-1=0\Rightarrow \lambda _{1}=1,\lambda _{2}=3$

我们通过上面求得该矩阵的2个特征值分别为1和3

$\bigl(\begin{smallmatrix} 2-1 &1 \\ 1 & 2-1 \end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} 1 &1 \\ 1 & 1 \end{smallmatrix}\bigr)\Rightarrow \bigl(\begin{smallmatrix} 1 &1 \\ 0 & 0 \end{smallmatrix}\bigr)$

上面通过矩阵化简可以得到解为 $k\left ( 1,-1 \right )^{T}$

同理3这个特征值对应 $\bigl(\begin{smallmatrix} 2-3 & 1\\ 1 & 2-3 \end{smallmatrix}\bigr)= \bigl(\begin{smallmatrix} -1 & 1\\ 1 & -1 \end{smallmatrix}\bigr)\Rightarrow \bigl(\begin{smallmatrix} -1 & 1\\ 0 & 0 \end{smallmatrix}\bigr)$ 的解为： $k\left ( 1,1 \right )^{T}$

所以特征向量分别是 $\left ( 1,-1 \right )^{T} , \left ( 1,1 \right )^{T}$

---------------------------------------------------------------------------------------------------------------------------------------------------------------

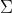这里的 $\Sigma$ 是一个对角矩阵，对角线上值就是所有的特征值，那么可以看到X最后可以根据（2）进行分解，一般的习惯 $VV^{T}=E$

所以 $V^{-1}=V^{T}$

------------------------------------------------------------------------------------------------------------------------------------------------------------------

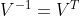
对应到上面的例子中特征向量应该是：

$\left ( \frac{1}{\sqrt{2}}, \frac{-1}{\sqrt{2}} \right )^{T} ,\left ( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right )^{T}$

注意当求矩阵单个特征值时是 $XV=\lambda V$ ，但当所有特征值放一起后是 $XV=V\Sigma$ 而不是 $XV=\Sigma V$ 这种形式。

即分解结果为： $\bigl(\begin{smallmatrix} 2 &1 \\ 1 & 2 \end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} \end{smallmatrix}\bigr)\bigl(\begin{smallmatrix} 3 &0 \\ 0 & 1 \end{smallmatrix}\bigr)\bigl(\begin{smallmatrix} \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} \end{smallmatrix}\bigr)$

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

（2）应用

在实际降维时，往往先要转化坐标轴，使坐标轴尽可能的覆盖多的数据，即找数据最大方差的位置，其往往给出了数据的最重要信息，比如找到后我们记该方向为x轴，那么其y轴就是与x轴垂直的方向。

所以思路就是找先将原始矩阵每一个元素减去其自身均值进行标准归一化，然后求得其协方差，最后再求协方差的特征值和特征向量，注意不是求原矩阵的特征值和特征向量。

---------------------------------------------------------------------------------------------------------------------------------------------------------------

好了，代码也应该很简单啦：

def pca(datamat,N=3):
    meanVals = mean(datamat,axis=0)
    meanRemoved = datamat - meanVals
    covmat = cov(meanRemoved,rowvar=0)
    eigVals,eigVects = linalg.eig(mat(covmat))
    eigValInd = argsort(eigVals)
    eigValInd = eigValInd[:-(N+1):-1]
    redEigVects = eigVects[:,eigValInd]
    lowDDataMat = meanRemoved*redEigVects
    reconMat = (lowDDataMat *redEigVects.T)+meanVals
    return lowDDataMat ,reconMat

就是在求出协方差的特征值后进行排序，然后选取前N名（eigValInd）特征值及其对应的特征向量（redEigVects）

然后lowDDataMat就是其将原始矩阵降维后，变成的新维度，该维度与原始矩阵相比，行数不变，列数降维到N，但却保留了原始矩阵所蕴含的大部分信息

reconMat就是我们用lowDDataMat来重构回原始矩阵，为什么会是这样呢?

$Cov = low\times red^{T}+meanVals=(meanRemoved\times red)\times red^{T}+meanVals=meanRemoved\times (red\times red^{T})+meanVals=meanRemoved+meanVals=datamat$

这里将 redEigVects 简写为red，证明过程使用到了上面所说的 $VV^{T}=E$

重构只是为了验证一下而已，我们真正想要的正是lowDDataMat即返回的第一个矩阵。即假设datamat是m*m,那么降维后便是m*N

-------------------------------------------------------------------------------------------------------------------------------------------------------------

但上面分解的前提是X必须为方阵那如果X不是方阵呢即是m*n，这时候SVD隆重登场

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

注意：上面的PCA的原始矩阵虽说可以不是方阵，但我们也不是求原始矩阵的特征值和特征向量呀，是求的其协方差，其协方差即 $cov = E((X-E(X)(X-E(X)^{T})$ 这里的协方差cov一定是方阵对吧，所以其本质还是对方阵进行的分解，而下面介绍的svd正是直接对不是方阵的情况进行分解

--------------------------------------------------------------------------------------------------------------------------------------------------------------------

SVD

(1)原理

首先看一下SVD矩阵分解公式：

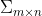$(3)X_{m\times n}= U_{m\times m} \Sigma_{m\times n} V_{n\times n}^{T}$

这里的 $\Sigma_{m\times n}$ 其实是一个对角矩阵，对角线上面的值就称为奇异值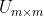， $U_{m\times m}$ 和 $V_{n\times n}$ 分别称为左奇异矩阵、右奇异矩阵

-------------------------------------------------------------------------------------------------------------------------------------------------------------------

对比一下方阵求特征值的公式：

（1）方阵分解那里对角线是特征值，这里是奇异值

（2）方阵分解那里左右维数相同，互为逆矩阵（ $V$ 和 $V^{-1}$ ）,而这里是左右奇异矩阵

可以看到这两种分解在形式上大体相似，只是维数不同

-------------------------------------------------------------------------------------------------------------------------------------------------------------

这里的 $U,\Sigma ,V$ 该怎么求呢？

先来看一下U：

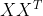$(XX^{T})v=\lambda v$ 我们求 $XX^{T}$ 的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是U

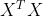$(X^{T}X)v=\lambda v$ 我们求 $X^{T}X$ 的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是V

注意这里我们将U和V中所有特征向量也进行了归一化，即 $UU^{T}=E , VV^{T}=E$

----------------------------------------------------------------------------------------------------------------------------------------------------------------

这里简单证明一下：

$(4)XX^{T}=U\Sigma V^{T}\times V\Sigma ^{T}U^{T}=U\Sigma ^{2}U^{T}\Rightarrow \left ( XX^{T} \right )U=U\Sigma ^{2}$

$(5)X^{T}X=V\Sigma ^{T}U^{T}\times U\Sigma V^{T}=V\Sigma ^{2}V^{T}\Rightarrow (X^{T}X)V=V\Sigma ^{2}$

通过（4）和（5）可以看到U和V其实分别就是 $XX^{T}$ 和 $X^{T}X$ 各自所有特征向量展开合并的矩阵

---------------------------------------------------------------------------------------------------------------------------------------------------------------

那么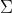 $\Sigma$ 怎么求呢，从上面的简单证明可以明显看出，其就是特征值的平方根，

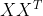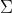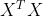好了最后总结一下，当我们拿到一个 $X_{m\times n}$ 矩阵需要分解时，首先是求 $XX^{T}$ 的特征值和对应的特征向量，将所有特征向量合并为一个矩阵，该矩阵就是U，给所有特征值开平方根就是奇异值，即得到 $\Sigma$ ，然后求 $X^{T}X$ 的特征值和特征向量，同样将所有特征向量合并为一个矩阵，该矩阵就是V（不难看到，其实两次的特征最后求得结果应该是一样的）

到这里我们就将SVD的分解原理叙述完毕啦，回头看看其实还是挺简单的对吧，下面来看看SVD的具体用途：

(2)应用

想PCA取前几个比较大的特征值一样，这里SVD是取前几个比较大奇异值

用的比较多的应该就是推荐系统里面的吧

假设现在有一个矩阵，每一行代表一个用户，每列代表一个物品

	辣条	薯片	可乐	冰红茶
小花	0	0	2	4
小明	0	0	2	5
小李	3	6	0	0

其中的数字是评价等级1~5 , 0代表没有评价

我们将该矩阵分解， $X_{3\times 4}=U_{3\times 3}\Sigma _{3\times 4}V_{4\times 4}\approx U_{3\times 2}\Sigma _{2\times 2}V_{2\times 4}$

这里假设我们取2个奇异值，那么便可以近似分解

可以看到原本是使用黄色来重构X，现在只使用红色就可以近似重构X，即达到了降维目的，那么这里的 $U_{3*2}$ 具体是什么含义呢？

它其实就是将每个用户映射到二维（原先是4维，分别代表辣条，薯片，可乐，冰红茶），在这两维中，小花和小明相似度相近，而小李

这位另一类，这和原始的评分矩阵反应出来的一样，即小花和小明相似度相近，而小李这位另一类，原先4个维度，现在我们只用2个维度就可以反应出同样的信息，这不就是降维了吗（至于这两个维度是什么新的含义呢？我们不必管，或是零食和饮料又或是其他的），总之这里对于每个用户来说，将原来的4维降为了2维，但其中还是包含原始原始矩阵的信息。同理 $V_{2\times 4}^{T}$ 是对每个物品来说，将原来的3维降为2维，即原始矩阵是这样的：每个物品下面有3个用户，而这里是，每个物品下面有2类人。

其实上面两种解释对应着两种不同的推荐策略：基于用户(客户数不变，即行数不变，压缩列数，归类物品)和基于物品(物品数不变，即列数不变，压缩行数，归类客户)。

在python中有现成的库可以用.来进行SVD矩阵分解，其返回的是三个矩阵，分别对应 $U,\Sigma ,V$

--------------------------------------------------------------------------------------------------------------------------------------------------------------

例如：

U,Z,V = linalg.svd(datamat)

这里的datamat就是我们要分解的矩阵。

现在比如一共求出有10个奇异值，我们取3个来进行降维，即我们要将原始矩阵的列数压缩到3维（也可以理解为对于每一个用户来说，原来是对很多商品进行了评价，现在我们要将其总结一下，使其结果是对总结后的3类商品进行的评价），即这里是求V:

$X=U\Sigma V^{T}\Rightarrow XV=U\Sigma \Rightarrow U=XV\Sigma ^{-1}$

假设原来datamat是15*10，那么降维后这里的X_tran就是15*3啦

同理如果是给行降维，即将人进行分类，就是说求V

$X=U\Sigma V^{T}\Rightarrow V^{T}=\Sigma ^{-1}U^{T}X\Rightarrow V=X^{T}U(\Sigma ^{-1})^{T}\Rightarrow V=X^{T}U(\Sigma ^{T})^{-1}\Rightarrow V=X^{T}U\Sigma ^{-1}$

X_tran = datamat.T*U[:,:3]*mat(eye(4)*U[:3]).I

假设原来datamat是15*10，那么降维后这里的X_tran就是3*10啦

--------------------------------------------------------------------------------------------------------------------------------------------------------------

现实中一般是行数对于列数（客户多，商品少），所以多采用基于商品，即要得到V

假设现在我们要给用户a推荐物品，那怎么做呢？

首先我们使用 $V=X^{T}U\Sigma ^{-1}$ 降维得到V，然后我们从datamat中先筛选出来客户a还没有买过的物品标号集合为R1，因为我们要从这里面挑出一些物品推荐给a,以及其评价过物品的集合R2，最后就是遍历R1，看其每一个物品和R2中每一个物品的相似度再乘以权重（即评价）

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------

可能上面说的有点不好理解，看一下代码吧，就好多啦：

代码参考;《机器学习实战》Peter Harrington著，李锐等译

def Similarity(datamat,user,simways,item):
    n = shape(datamat)[1]
    simTotal = 0.0
    ratSimTotal = 0.0
    U,Z,V = linalg.svd(datamat)
    X_tran = datamat.T*U[:,:3]*mat(eye(4)*U[:3]).I 
    for j in range(n):
        userRating = datamat[user,j]
        if userRating==0 or j==item:
            continue
        similarity = simways(X_tran[item,:].T,(X_tran[j,:].T)
        simTotal += similarity
        ratSimTotal +=similarity * userRating
     if simTotal=0:
         return 0
     else:
         return ratSimTotal/simTotal

上面的函数有四个输入，原始矩阵，要给哪个用户推荐，计算相似度的方法，以及当前推荐物品的id

从中可以看到我们取了3个奇异值

 X_tran = datamat.T*U[:,:3]*mat(eye(4)*U[:3]).I

对应我们求V的过程，即X_tran就是我们取3个奇异值后对应的V

if userRating==0 or j==item:
            continue

对应部分就是说要计算item和已经评过分的物品的相似度，加入j之前也没评价过，那比较就没有意义啦，这里就相当于上面我们说的处理出R2的过程

similarity = simways(X_tran[item,:].T,(X_tran[j,:].T)

部分就是求两个向量的相似度

ratSimTotal +=similarity * userRating

部分就是相似度乘以权重，不难想象，如果j的评分高，则userRating高，权重大，此时如果相似度也高，那么最后结果也高，如果j的评分底，相似度高，相当于带来的惩罚也越多（和评分差的相似度高，当然要给与高惩罚）

return ratSimTotal/simTotal

部分就是将结果该归一化到1~5评分等级中

好啦！！！！！！！！！！！！！！！！！

有了上面的评分函数，接下来就是在外面遍历R1就可以啦

def recommend(datamat,user,N=3,simways):
    unratedItems = nonzero(datamat[user,:].A==0)[1]
    if len(unratedItems) == 0:
        return 'you rated everything'
    itemScores = []
    for item in unratedItems:
        estimatedScore = Similarity(datamat,user,simways,item)
        itemScores.append((item, estimatedScore))
    return sorted(itemScores,key=lambda x:x[1],reverse=True)[:N]

这里的 unratedItems就是我们上面讨论的R1集合，N参数就是我们要给该用户推荐物品的个数

--------------------------------------------------------------------------------------------------------------------------------------------------------

关于上面的simways即相似度的量化方法有很多，比较容易相当的就是欧式距离和余弦相似度，除此之外的就是皮尔逊相关系数，本文主要讲解SVD，这里就不展开说明相似度的事情啦，网上搜索一下，都很简单。

最后说一下两者的联系，其实svd可以用来做pca的，因为在pca阶段我们主要求得是 $XX^{T}$ 特征值和特征向量，对吧（暂不考虑减去均值），而在求svd的左奇异矩阵（U）过程中，也是求得是 $XX^{T}$ 特征值和特征向量对吧，也就是说这里的SVD奇异值的平方就是pca中的特征值对吧，其实在SVD的分解过程中，不用像我们上面讨论的那样先求 $XX^{T}$ ， $X^{T}X$ 特征值和特征向量方法进行分解，而是有很多快速算法，但我们可以根据SVD的结果进行PCA对吧，其实scikit-learn内部的PCA也是用SVD做的

PCA SVD原理详解及应用

本文分为两大部分即PCA和SVD，每一部分下又分为原理和应用两小部分

说明：本文代码参考Peter Harrington编写的Machine Learning in Action,感兴趣的小伙伴可以去看一下，笔者认为这本书还不错

废话不多说开始吧

PCA:

$(1)XV=\lambda V$

$(2)XV=V\Sigma \Rightarrow X=V\Sigma V^{-1}=V\Sigma V^{T}$

公式（1）是我们熟悉的求特征值的式子，假设X是m*m，我们根据其求出了 $\lambda _{1},\lambda _{2},\cdots \lambda _{m}$ 特征值以及每个特征值对应的特征向量。

这里的 $\Sigma$ 是一个对角矩阵，对角线上值就是所有的特征值，那么可以看到X最后可以根据（2）进行分解，一般的习惯 $VV^{T}=E$

所以 $V^{-1}=V^{T}$

在实际降维时，往往先要转化坐标轴，使坐标轴尽可能的覆盖多的数据，即找数据最大方差的位置，其往往给出了数据的最重要信息，比如找到后我们记该方向为x轴，那么其y轴就是与x轴垂直的方向。

所以思路就是找先将原始矩阵每一个元素减去其自身均值进行标准归一化，然后求得其协方差，最后再求协方差的特征值和特征向量，注意不是求原矩阵的特征值和特征向量。

但上面分解的前提是X必须为方阵那如果X不是方阵呢即是m*n，这时候SVD隆重登场

SVD

首先看一下SVD矩阵分解公式：

$(3)X_{m\times n}= U_{m\times m} \Sigma_{m\times n} V_{n\times n}^{T}$

这里的 $\Sigma_{m\times n}$ 其实是一个对角矩阵，对角线上面的值就称为奇异值， $U_{m\times m}$ 和 $V_{n\times n}$ 分别称为左奇异矩阵、右奇异矩阵

这里的 $U,\Sigma ,V$ 该怎么求呢？

先来看一下U：

$(XX^{T})v=\lambda v$ 我们求 $XX^{T}$ 的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是U

$(X^{T}X)v=\lambda v$ 我们求 $X^{T}X$ 的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是V

注意这里我们将U和V中所有特征向量也进行了归一化，即 $UU^{T}=E , VV^{T}=E$

那么 $\Sigma$ 怎么求呢，从上面的简单证明可以明显看出，其就是特征值的平方根，

到这里我们就将SVD的分解原理叙述完毕啦，回头看看其实还是挺简单的对吧，下面来看看SVD的具体用途：

用的比较多的应该就是推荐系统里面的吧

可以看到原本是使用黄色来重构X，现在只使用红色就可以近似重构X，即达到了降维目的，那么这里的 $U_{3*2}$ 具体是什么含义呢？

它其实就是将每个用户映射到二维（原先是4维，分别代表辣条，薯片，可乐，冰红茶），在这两维中，小花和小明相似度相近，而小李

其实上面两种解释对应着两种不同的推荐策略：基于用户(客户数不变，即行数不变，压缩列数，归类物品)和基于物品(物品数不变，即列数不变，压缩行数，归类客户)。

在python中有现成的库可以用.来进行SVD矩阵分解，其返回的是三个矩阵，分别对应 $U,\Sigma ,V$

现实中一般是行数对于列数（客户多，商品少），所以多采用基于商品，即要得到V

假设现在我们要给用户a推荐物品，那怎么做呢？

关于上面的simways即相似度的量化方法有很多，比较容易相当的就是欧式距离和余弦相似度，除此之外的就是皮尔逊相关系数，本文主要讲解SVD，这里就不展开说明相似度的事情啦，网上搜索一下，都很简单。

结束啦！！！！！哪里有不对还望大佬指正

猜你喜欢

PCA SVD原理详解及应用

本文分为两大部分即PCA和SVD，每一部分下又分为原理和应用两小部分

说明：本文代码参考Peter Harrington编写的Machine Learning in Action,感兴趣的小伙伴可以去看一下，笔者认为这本书还不错

废话不多说开始吧

PCA:

公式（1）是我们熟悉的求特征值的式子，假设X是m*m，我们根据其求出了特征值以及每个特征值对应的特征向量。

这里的是一个对角矩阵，对角线上值就是所有的特征值，那么可以看到X最后可以根据（2）进行分解，一般的习惯

所以

在实际降维时，往往先要转化坐标轴，使坐标轴尽可能的覆盖多的数据，即找数据最大方差的位置，其往往给出了数据的最重要信息，比如找到后我们记该方向为x轴，那么其y轴就是与x轴垂直的方向。

所以思路就是找先将原始矩阵每一个元素减去其自身均值进行标准归一化，然后求得其协方差，最后再求协方差的特征值和特征向量，注意不是求原矩阵的特征值和特征向量。

但上面分解的前提是X必须为方阵那如果X不是方阵呢即是m*n，这时候SVD隆重登场

SVD

首先看一下SVD矩阵分解公式：

这里的其实是一个对角矩阵，对角线上面的值就称为奇异值，和分别称为左奇异矩阵、右奇异矩阵

这里的该怎么求呢？

先来看一下U：

我们求的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是U

我们求的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是V

注意这里我们将U和V中所有特征向量也进行了归一化，即

那么怎么求呢，从上面的简单证明可以明显看出，其就是特征值的平方根，

到这里我们就将SVD的分解原理叙述完毕啦，回头看看其实还是挺简单的对吧，下面来看看SVD的具体用途：

用的比较多的应该就是推荐系统里面的吧

可以看到原本是使用黄色来重构X，现在只使用红色就可以近似重构X，即达到了降维目的，那么这里的具体是什么含义呢？

它其实就是将每个用户映射到二维（原先是4维，分别代表辣条，薯片，可乐，冰红茶），在这两维中，小花和小明相似度相近，而小李

其实上面两种解释对应着两种不同的推荐策略：基于用户(客户数不变，即行数不变，压缩列数，归类物品)和基于物品(物品数不变，即列数不变，压缩行数，归类客户)。

在python中有现成的库可以用.来进行SVD矩阵分解，其返回的是三个矩阵，分别对应

现实中一般是行数对于列数（客户多，商品少），所以多采用基于商品，即要得到V

假设现在我们要给用户a推荐物品，那怎么做呢？

关于上面的simways即相似度的量化方法有很多，比较容易相当的就是欧式距离和余弦相似度，除此之外的就是皮尔逊相关系数，本文主要讲解SVD，这里就不展开说明相似度的事情啦，网上搜索一下，都很简单。

结束啦！！！！！哪里有不对还望大佬指正

猜你喜欢

公式（1）是我们熟悉的求特征值的式子，假设X是m*m，我们根据其求出了 $\lambda _{1},\lambda _{2},\cdots \lambda _{m}$ 特征值以及每个特征值对应的特征向量。

这里的 $\Sigma$ 是一个对角矩阵，对角线上值就是所有的特征值，那么可以看到X最后可以根据（2）进行分解，一般的习惯 $VV^{T}=E$

所以 $V^{-1}=V^{T}$

这里的 $\Sigma_{m\times n}$ 其实是一个对角矩阵，对角线上面的值就称为奇异值， $U_{m\times m}$ 和 $V_{n\times n}$ 分别称为左奇异矩阵、右奇异矩阵

这里的 $U,\Sigma ,V$ 该怎么求呢？

$(XX^{T})v=\lambda v$ 我们求 $XX^{T}$ 的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是U

$(X^{T}X)v=\lambda v$ 我们求 $X^{T}X$ 的特征值和特征向量，然后将所有的特征向量展开放到一个矩阵，该矩阵就是V

注意这里我们将U和V中所有特征向量也进行了归一化，即 $UU^{T}=E , VV^{T}=E$

那么 $\Sigma$ 怎么求呢，从上面的简单证明可以明显看出，其就是特征值的平方根，

可以看到原本是使用黄色来重构X，现在只使用红色就可以近似重构X，即达到了降维目的，那么这里的 $U_{3*2}$ 具体是什么含义呢？

在python中有现成的库可以用.来进行SVD矩阵分解，其返回的是三个矩阵，分别对应 $U,\Sigma ,V$