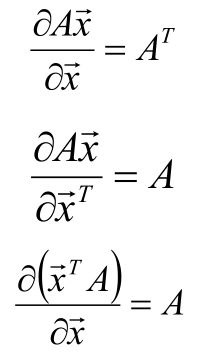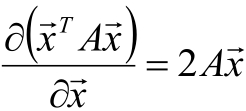数据挖掘--PCA原理

一、PCA原理：

•主成分分析（Principal Components Analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

算法流程：

输入：n为样本集 $D=(x^{(1)}, x^{(2)},...,x^{(m)})$ ，设为 X，需要降维到 ${n}'$

输出：降维后的样本集 ${D}'$

（1）先对所有的数据集进行中心化： $x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}$

（2）计算样本的协方差矩阵： $XX^{T}$

（3）对协方差矩阵进行求特征值和特征向量

（4）取出 ${n}'$ 个最大的特征值对应的特征向量 $(w_1,w_2,...,w_{n'})$ ，将所有的特征向量标准化，组成新的矩阵 w

（5）输出矩阵：Y= WX 即为降维到 ${n}'$ 维后的数据

基于最大投影方差：

假设m个n维数据 $(x^{(1)}, x^{(2)},...,x^{(m)})$ 都已经对其进行中心化处理了， $\sum\limits_{i=1}^{m}x^{(i)}=0$ ，经过投影变换后得到的新坐标系为 $(w_1,w_2,...,w_{n'})$ ,其中w 是标准正交基，即 $||w||_2=1, w_i^Tw_j=0$ 。

如果我们将数据从n维降到n'维，即丢弃新坐标系中的部分坐标，则新的坐标系为 $\{w_1,w_2,...,w_{n'}\}$ ,样本点x(i)在n'维坐标系中的投影为： $z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})$ .其中， $z_j^{(i)} = w_j^Tx^{(i)}$ 是x(i)在低维坐标系里第j维的坐标。

对于任意一个样本x(i)，在新的坐标系中的投影为 $W^Tx^{(i)}$ ,在新坐标系中的投影方差为 $W^Tx^{(i)}x^{(i)T}W$ ，要使所有的样本的投影方差和最大，也就是最大化 $\sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}W$ ,即：

$\underbrace{arg\;max}_{W}\;tr( W^TXX^TW) \;\;s.t. W^TW=I$

u1方向上的投影的绝对值之和最大（也可以说方差最大），就是将x与u1做内积。将u1标准化为单位向量。

使用拉格朗日函数可以得到：

$J(W) = tr( W^TXX^TW) + \lambda(W^TW-I)$

对W求导有 $XX^TW+\lambda W=0$ , 整理下即为：

$XX^TW=\left ( -\lambda \right )W$

对W 的求导可以把 $W^{T}W=W^{T}E W$ , 然后再使用下面的公式进行求导，两边都有个2 ，可以约去。

对于矩阵的求导可以参考：https://blog.csdn.net/xueyingxue001/article/details/51829718

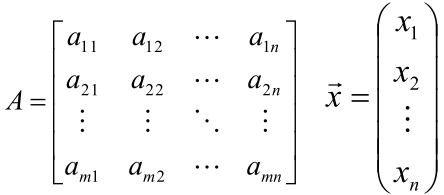
几个常用的向量求导公式：

如果 y = xT·A·x的话，y对向量x求偏导的结果是

如果这时A有时对称阵，则：

由于协方差矩阵是对称的，因此其特征向量正交。最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。

如果数据集是100 X 10，100行10列的，需要保留4个特征量，即选出4个最大的特征值，使原数据（100 X 10）* （10 X 4）=（100 X 4 ），10乘4 代表4个重要的特征向量聚合。

参考：https://blog.csdn.net/zhongkelee/article/details/44064401此文章讲的比较详细

http://www.cnblogs.com/pinard/p/6239403.html

数据挖掘--PCA原理

一、PCA原理：

猜你喜欢