1.Principal components analysis（主成分分析）

1.1Principal components analysis 基本原理

首先我们先来看主成分分析的步骤：
假设我们有P个n维数据样本D，样本的值为[V1,V2,…,Vn]要把他们降维到m维（m<n）
（1）求出所有数据样本的平均值 $\overline S=1/n\sum_{i=1}^{n}V_i$ ，对所有数据进行中心化 $X_i=X_i-\overline S$
（2）计算数据样本的协方差矩阵 $Cov(x_1 ,x_2,...,x_n)=XX^T= \left[\begin{matrix} cov(x_1,x_2)&...&cov(x_1,x_n)\\...&...&...\\cov(x_n,x_1)&...&cov(x_n,x_n) \end{matrix} \right](n*n维)$

$conv（X，Y）=E(X-EX)（Y-EY）=1/n-1\sum_{i=1}^n(x_i-\overline x)(y_i-\overline y)$

协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上是协方差矩阵(对称方阵).

（3）对协方差矩阵 $XX^T$ 进行特征分解
（4）取出最大的m个特征值并求出相应的特征向量组成W $(w_1,w_2,...,w_m)$ ,将W矩阵单位化后形成特征向量矩阵W
（5）对P个样本转化为 $P_{new}$ , $P_{new}$ = $W \odot P$

$W=\left[\begin{matrix}w_1,w_2,...,w_m \end{matrix} \right]$ , 维度信息：” $(m,n) \times (n,1)=(m,1)$

（6）得到P个m维新的数据样本

1.2 Example

**假设我们的数据集有10个二维数据(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)，需要用PCA降到1维特征。
　　　　首先我们对样本中心化，这里样本的均值为(1.81, 1.91),所有的样本减去这个均值后，即中心化后的数据集为(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。
　　　　现在我们开始求样本的协方差矩阵，由于我们是二维的，则协方差矩阵为：
XXT=(cov(x1,x1)cov(x2,x1)cov(x1,x2)cov(x2,x2))
　　　　对于我们的数据，求出协方差矩阵为：
XXT=(0.6165555560.6154444440.6154444440.716555556)
　　　　求出特征值为（0.0490833989， 1.28402771），对应的特征向量分别为：(0.735178656,0.677873399)T(−0.677873399,−0.735178656)T,由于最大的k=1个特征值为1.28402771，对于的k=1个特征向量为(−0.677873399,−0.735178656)T. 则我们的W=(−0.677873399,−0.735178656)T
　　　　我们对所有的数据集进行投影z(i)=WTx(i)，得到PCA降维后的10个一维数据集为：(-0.827970186， 1.77758033， -0.992197494， -0.274210416， -1.67580142， -0.912949103， 0.0991094375， 1.14457216, 0.438046137， 1.22382056) **

1.3 PCA的优缺点

1.优点：
（1）PCA分析仅仅需要在数据集内计算平均值，方差等信息，不受数据集外任何条件的约束。
（2）PCA分析各主成分之间是相互正交的，可消除成分之间信息的影响。
（3）PCA保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。
2.缺点：
（1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
（2）方差小的特征也可能含有样本差异的重要信息，直接降维丢弃很可惜。

1.4 PCA的Python实现

import numpy as np

def pca(X,k):#k is the components you want
  #mean of each feature
  n_samples, n_features = X.shape
  mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
  #normalization
  norm_X=X-mean
  #scatter matrix
  scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
  #Calculate the eigenvectors and eigenvalues
  eig_val, eig_vec = np.linalg.eig(scatter_matrix)
  eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
  # sort eig_vec based on eig_val from highest to lowest
  eig_pairs.sort(reverse=True)
  # select the top k eig_vec
  feature=np.array([ele[1] for ele in eig_pairs[:k]])
  #get new data
  data=np.dot(norm_X,np.transpose(feature))
  return data
 
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
 
print(pca(X,1))

代码原文链接

2.Singular Value Decomposition（奇异值分解）

2.1 Singular Value Decomposition 基本原理

1.首先先说一下用到的基本线代基础：
（1）对n阶方阵A，如果可以找到可逆矩阵P使得 $P^{-1}AP=\Lambda$ ,那么我们就可以说A矩阵可以相似对角化
1>. A有n个不同的特征值.
2>.A的 $t_i$ 重特征值对应的线性无关的特征向量
（2）矩阵相似对角化为 $\Lambda$ 可以简化矩阵之间的运算并且通过特征值和特征向量可以反求出矩阵A
（3）一般我们会把W的这n个特征向量标准化，即满足||wi||2=1, 或者说wTiwi=1，此时W的n个特征向量为标准正交基，满足WTW=I，即WT=W−1, 也就是说W为正交矩阵
（4）注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了

2.进入SVD正题：
SVD也是矩阵分解的一种方式但是它并不要求分解矩阵必须为方阵
$SVD:A=U\Lambda V^T$
** $其中U矩阵维度为 m \times m$ ， $\Lambda 的维度为m\times n$ , $V^T的维度为n\times n$ ,其中U，V均为正交矩阵表示为 $UU^T=E,VV^T=E$ ,如下图所示：
在这里插入图片描述

1.首先我们从A矩阵中要得到一个方阵 $AA^T$ ，既然已经得到方阵我们可以对方阵进行特征分解满足 $AA^T v_i = \lambda _iv_i$ 就得到了 $AA^T$ 的特征值和特征向量.
2.特征值对应的特征向量拼成了矩阵V，一般我们将V中的每个特征向量叫做A的左奇异向量
3.首先我们从A矩阵中要得到一个方阵 $A^TA$ ，既然已经得到方阵我们可以对方阵进行特征分解满足 $A^TA v_i = \lambda _iv_i$ 就得到了 $A^TA$ 的特征值和特征向量.
4.特征值对应的特征向量拼成了矩阵U，一般我们将U中的每个特征向量叫做A的右奇异向量
5.接下来就是奇异值矩阵了
$A=U\Lambda V^T ,AV=U\Lambda ,Av_i=u_i\Lambda ,\Lambda=A\odot v_i/u_i$
其实奇异值矩阵就是左奇异值和右奇异值的开根号， $\Lambda=\left[\begin{matrix} \sqrt{v_1}&&&\\&\sqrt{v_2} &&\\&&...&&\\&&&\sqrt{u_i}\end{matrix}\right]$

(1) 求 $AA^T$ 的特征值和特征向量，用单位化的特征向量构成 U。
(2) 求 $AA^T$ 的特征值和特征向量，用单位化的特征向量构成 V。
(3) 将 $AA^T$ 或者 $A^TA$ 的特征值求平方根，然后构成 $\Lambda$ 。

2.2 Example

在这里插入图片描述

2.3 SVD，PCA的区别和类似

1. SVD可以获取另一个方向上的主成分，而PCA只能获得单个方向上的主成分
2.隐语义索引（Latent semantic indexing，简称LSI）通常建立在SVD的基础上，通过低秩逼近达到降维的目的。
3.PCA也能达到降维的目的，但是PCA需要进行零均值化，且丢失了矩阵的稀疏性
4.通过SVD可以得到PCA相同的结果，但是SVD通常比直接使用PCA更稳定。因为PCA需要计算X⊤X的值，对于某些矩阵，求协方差时很可能会丢失一些精度。
5.SVD一般是用来诊断两个场的相关关系的，而PCA是用来提取一个场的主要信息的（即主分量）
6.为什么使用PCA而不是SVD：转成协方差矩阵，是对称矩阵，特征值分解比SVD奇异值分解的计算量小的多

3.张量分解

3.1 Tensor Decomposition

**1.由于高阶张量的性质和应用需求，我们使用张量特征值和张量分解，使用张量分解可以保持数据内在结构不仅可以避免损失重要的信息也是解决实际问题的需要。
2.张量分解可以保持数据集中的对方差贡献的最大特征同时减少数据的维度，张量分解是矩阵奇异值分解在多重线性代数的高阶推广.
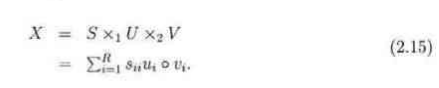
在这里插入图片描述
3.式子2.15表示一个张量X分解为一个对角核张量和两个正交矩阵U,V的1模式和2模式的乘积但是高阶张量不能保证同时有对角核张量和正交矩阵以至于全部分解为2.15的格式所以有了CP分解和Tucker分解.

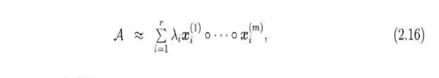
4.CP分解保持了核张量的对角性将m阶张量分解为r个秩1张量的线性组合。||Xi||=1。
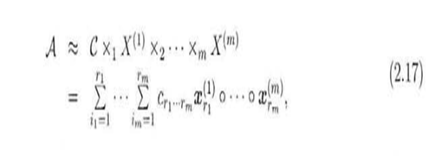
在这里插入图片描述
5.Trucker分解保持了因子的正交性。当r1，r2,…,rm相等时并且因子矩阵是对角化Trucker分解就可以表示为特殊的CP分解.