PCA原理小结

　　主成分分析（Principal Component Analysis，PCA）是最常用的一种数据降维方法。顾名思义，PCA就是找出原始数据中最主要的方面来表示原始数据，可以获得比原始输入维度更低的表示。具体来说，假设原始数据 $X=\{x^{(1)},x^{(2)},\dots,x^{(m)}\}$ ， $x^{(i)}$ 是 $d$ 维向量，我们现在希望将每个样本 $x^{(i)}$ 从 $d$ 维降到 $d'$ 维（ $d'<d$ ），并且希望新的 $d'$ 维数据能尽可能代表原始数据。显然，数据降维之后肯定会有数据损失，如何将这个损失降到最小就是PCA要解决的问题了。

1. PCA的直观理解

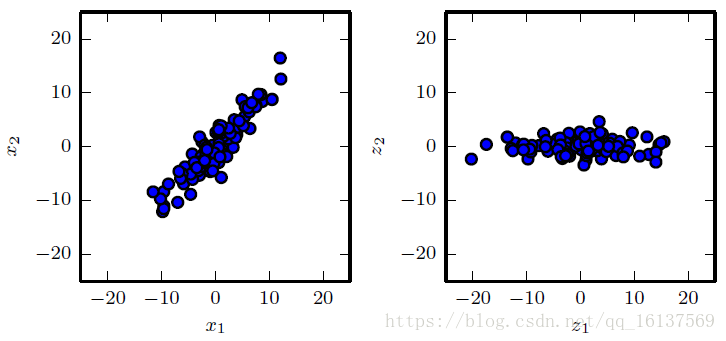
　　我们不妨先考虑这样一个问题：对于正交属性空间中的样本点，如何用一个超平面对所有样本进行恰当的表达？

　　首先我们要明确什么叫做“恰当的表达”。以上图为例，左图中的二维数据中样本几乎都是沿着 $x_2=x_1$ 方向分布， $x_1$ 和 $x_2$ 存在着很明显的相关性，样本点在 $x_1$ 和 $x_2$ 两个方向变化幅度相当，所以如果要区分各个样本点， $x_1$ 和 $x_2$ 缺一不可，缺少其中一个都有可能出现丢失大量数据的情况。如果我们将原始坐标系旋转 $45^\circ$ ，得到右图坐标系 $(z_1,z_2)$ ，现在样本点几乎沿着 $z_1$ 方向分布了，在 $z_2$ 方向不同样本点几乎没有差别，因此去掉 $z_2$ 也影响不大。这里 $z_1$ 其实就对应这数据的第一个主要成分，我们用 $z_1$ 就能表达绝大部分数据。
　　然后再回到本节开始的问题，如果存在这样的超平面，那么它大概存在什么样的性质呢？从上图中的例子我们归纳：
　　(1) 最近重构性：样本点到这个超平面的距离都足够近
　　(2) 最大可分性：样本点在这个超平面上的投影能尽可能分开
　　其实用一句话总结就是，PCA学习了一种元素之间彼此没有线性相关的表示。从上图中也可以看出，相比 $(x_1,x_2)$ 坐标系表达， $(z_1,z_2)$ 坐标系两个轴的相关性明显低得多甚至可以忽略。基于上面的最近重构性和最大可分性，可以得到PCA两种不同的等价推导。

2. PCA推导

　　假设 $m$ 个 $d$ 维数据 $(x^{(1)},x^{(2)},\dots,x^{(m)})$ 都已经进行了中心化，即 $\sum_{i=1}^mx^{(i)}=0$ 。经过投影变换后得到的新坐标系为 $\{w_1,w_2,\dots,w_d\}$ ，其中 $w_i$ 是标准正交基， $\|w_i\|_2=1,w_i^Tw_j=0(i \ne j)$ 。如果我们将数据从 $d$ 维降到 $d'$ 维，即丢弃新坐标系中的部分坐标，则样本点 $x^{(i)}$ 在新坐标系中的投影为 $z^{(i)}=(z^{(i)}_1,z^{(i)}_2,\dots,z^{(i)}_{d'})$ ，其中 $z^{(i)}_j=w_j^Tx^{(i)}$ 是 $x^{(i)}$ 在低维新坐标系下第 $j$ 维的坐标。那么新坐标 $z^{(i)}$ 和旧坐标 $x^{(i)}$ 的映射关系为

\begin{matrix} (1) & z^{(i)} = W^{T} x^{(i)} \end{matrix}

$z^{(i)}=W^Tx^{(i)}\tag{1}$ 其中

W

$W$ 为

d^{'}

$d'$ 个标准正交基组成的矩阵。如果基于

z^{(i)}

$z^{(i)}$ 来重构

x^{(i)}

$x^{(i)}$ ，有

\begin{matrix} (2) & {\hat{x}}^{(i)} = \sum_{j = 1}^{d^{'}} z_{j}^{(i)} w_{j} = W z^{(i)} \end{matrix}

$\hat{x}^{(i)}=\sum_{j=1}^{d'}z^{(i)}_jw_j=Wz^{(i)}\tag{2}$

最近重构性推导

　　最近重构性是指样本点到这个超平面的距离足够近，即通过主成分重构得到的 $\hat{x}^{(i)}$ 和原始样本点 $x^{(i)}$ 的距离尽可能小。也可以从另外一个角度理解：降维后的数据要尽可能接近原始数据。考虑整个训练集，重构得到的 $\hat{x}^{(i)}$ 和原始样本点 $x^{(i)}$ 的距离平方和为

\begin{aligned} \sum_{i = 1}^{m} ‖ {\hat{x}}^{(i)} - x^{(i)} ‖_{2}^{2} & = \sum_{i = 1}^{m} ‖ W z^{(i)} - x^{(i)} ‖_{2}^{2} \\ = \sum_{i = 1}^{m} (W z^{(i)})^{T} (W z^{(i)}) - 2 \sum_{i = 1}^{m} (W z^{(i)})^{T} x^{(i)} + \sum_{i = 1}^{m} x^{(i) T} x^{(i)} \\ = \sum_{i = 1}^{m} z^{(i) T} W^{T} W z^{(i)} - 2 \sum_{i = 1}^{m} z^{(i) T} W^{T} x^{(i)} + \sum_{i = 1}^{m} x^{(i) T} x^{(i)} \\ = \sum_{i = 1}^{m} z^{(i) T} z^{(i)} - 2 \sum_{i = 1}^{m} z^{(i) T} z^{(i)} + \sum_{i = 1}^{m} x^{(i) T} x^{(i)} \\ = - \sum_{i = 1}^{m} z^{(i) T} z^{(i)} + \sum_{i = 1}^{m} x^{(i) T} x^{(i)} \\ = - t r (W^{T} \sum_{i = 1}^{m} (x^{(i)} x^{(i) T}) W) + \sum_{i = 1}^{m} x^{(i) T} x^{(i)} \\ = - t r (W^{T} X X^{T} W) + \sum_{i = 1}^{m} x^{(i) T} x^{(i)} \end{aligned}

$\begin{align*}\sum_{i=1}^m\|\hat{x}^{(i)}-x^{(i)}\|_2^2 &=\sum_{i=1}^m\|Wz^{(i)}-x^{(i)}\|_2^2 \\&=\sum_{i=1}^m(Wz^{(i)})^T(Wz^{(i)})-2\sum_{i=1}^m(Wz^{(i)})^Tx^{(i)}+\sum_{i=1}^mx^{(i)T}x^{(i)}\\&=\sum_{i=1}^mz^{(i)T}W^TWz^{(i)}-2\sum_{i=1}^mz^{(i)T}W^Tx^{(i)}+\sum_{i=1}^mx^{(i)T}x^{(i)}\\&=\sum_{i=1}^mz^{(i)T}z^{(i)}-2\sum_{i=1}^mz^{(i)T}z^{(i)}+\sum_{i=1}^mx^{(i)T}x^{(i)}\\&=-\sum_{i=1}^mz^{(i)T}z^{(i)}+\sum_{i=1}^mx^{(i)T}x^{(i)}\\&=-\mathrm{tr}(W^T\sum_{i=1}^m(x^{(i)}x^{(i)T})W)+\sum_{i=1}^mx^{(i)T}x^{(i)}\\&=-\mathrm{tr}(W^TXX^TW)+\sum_{i=1}^mx^{(i)T}x^{(i)}\end{align*}$ 因此最小化

\sum_{i = 1}^{m} ‖ {\hat{x}}^{(i)} - x^{(i)} ‖_{2}^{2}

$\sum_{i=1}^m\|\hat{x}^{(i)}-x^{(i)}\|_2^2$ 等价于下面的约束优化问题：

\begin{matrix} (3) & \arg min_{W} - t r (W^{T} X X^{T} W), s . t . W^{T} W = I \end{matrix}

$\arg\min_W-\mathrm{tr}(W^TXX^TW),　s.t.　W^TW=I\tag{3}$ 这个问题想必大家很熟悉了，用拉格朗日乘子法可得对应的拉格朗日函数为

\begin{matrix} (4) & L (W, λ) = - t r (W^{T} X X^{T} W) + λ (W^{T} W - I) \end{matrix}

$L(W,\lambda)=-\mathrm{tr}(W^TXX^TW)+\lambda(W^TW-I)\tag{4}$ 然后就化为对偶问题

max_{λ} min_{W} L (W, λ)

$\max_{\lambda}\min_WL(W,\lambda)$ 将

L (W, b)

$L(W,b)$ 对

W

$W$ 求导，得:

- 2 X X^{T} W + 2 λ W = 0

$-2XX^TW+2\lambda W=0$ 整理一下，即

\begin{matrix} (5) & X X^{T} W = λ W \end{matrix}

$XX^TW=\lambda W\tag{5}$ 然后这不就是特征值的定义式吗？所以只需要对协方差矩阵

W^{T} W

$W^TW$ 进行特征值分解，并将求得的特征值排序

λ_{1} \geq λ_{2} \geq \dots \geq λ_{d}

$\lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_d$ ，再取前

d^{'}

$d'$ 个特征值对应的向量构成

W^{*} = (w_{1}, w_{2}, \dots, w_{d^{'}})

$W^*=(w_1,w_2,\dots,w_{d'})$ ，这就是PCA的解。

最大可分性推导

　　下面再来看一下最大可分性怎么推导出PCA。样本点在超平面上投影尽可能分开等价于投影后样本点的方差最大化。投影后样本点的方差为 $\sum_{i=1}^mW^Tx^{(i)}x^{(i)T}W$ ，于是优化目标可以写为

\begin{matrix} (6) & \arg max_{W} t r (W^{T} X X^{T} W), s . t . W^{T} W = I \end{matrix}

$\arg\max_W\mathrm{tr}(W^TXX^TW),　s.t.　W^TW=I\tag{6}$ 不难发现，这个优化目标和(3)是等价的，所以也能得到(5)的结论。下面就不赘述了。

3. PCA算法流程

　　先梳理一下PCA的算法流程，然后最后再来讨论一下PCA的性质。
　　假设原始数据 $X=\{x^{(1)},x^{(2)},\dots,x^{(m)}\}$ ， $x^{(i)}$ 是 $d$ 维向量，我们现在希望将每个样本 $x^{(i)}$ 从 $d$ 维降到 $d'$ 维（ $d'<d$ ）。
输入： $d$ 维数据集 $X=\{x^{(1)},x^{(2)},\dots,x^{(m)}\}$ ，要降到的维数 $d'$
输出：降维后的数据集 $X'$
Step1: 对所有样本进行中心化

x^{(i)} = x^{(i)} - \frac{1}{m} \sum_{j = 1}^{m} x^{(j)}

$x^{(i)}=x^{(i)}-\frac{1}{m}\sum_{j=1}^mx^{(j)}$ Step2: 计算样本的协方差矩阵

X^{T} X

$X^TX$ （严格来说协方差矩阵还有一个

\frac{1}{m - 1}

$\frac{1}{m-1}$ 的常数项，不过不影响结果，可以省去）；
Step3: 对协方差矩阵

X^{T} X

$X^TX$ 进行特征值分解/奇异值分解，得到特征值

λ_{i}

$\lambda_i$ 及其对应的特征向量

w_{i}

$w_i$ ，

i = 1, 2, \dots, d

$i=1,2,\dots,d$ ；
Step4: 取前

d^{'}

$d'$ 大个特征值对应的特征向量

(w_{1}, w_{2}, \dots, w_{d^{'}})

$(w_1,w_2,\dots,w_{d'})$ ，标准化后构成特征向量矩阵

W

$W$ ；
Step5: 根据特征向量矩阵

W

$W$ 计算出原始数据

x^{(i)}

$x^{(i)}$ 在特征空间中的投影

z^{(i)}

$z^{(i)}$ ：

z^{(i)} = W^{T} x^{(i)}

$z^{(i)}=W^Tx^{(i)}$ 从而得到原始数据在特征空间中的降维表示

X^{'} = (z^{(1)}, z^{(2)}, \dots, z^{(m)})

$X'=(z^{(1)},z^{(2)},\dots,z^{(m)})$ 。如果需要基于

z^{(i)}

$z^{(i)}$ 来重构

x^{(i)}

$x^{(i)}$ ，可以根据这个式子来(其实就是将上一个等式都左乘一个

W^{T}

$W^T$ 的逆)

{\hat{x}}^{(i)} = \sum_{j = 1}^{d^{'}} z_{j}^{(i)} w_{j} = W z^{(i)}

$\hat{x}^{(i)}=\sum_{j=1}^{d'}z^{(i)}_jw_j=Wz^{(i)}$
　　关于低维空间维度

d^{'}

$d'$ 的选择，通常情况下是用户事先指定的；或对不同

d^{'}

$d'$ 进行交叉验证然后选择最优的；或设置一个重构阈值

t

$t$ ，然后选取使下式成立的最小

d^{'}

$d'$ 值：

\frac{\sum_{i = 1}^{d^{'}} λ_{i}}{\sum_{i = 1}^{d} λ_{i}} \geq t

$\frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i}\ge t$

4. PCA的性质

PCA降维舍弃的这部分信息往往是必要的：一方面，舍弃这部分信息之后能使样本的采样密度增大，这正是降维的重要动机；另一方面，当数据受噪声影响时，最小的特征值所对应的特征向量往往和噪声有关，舍弃它们在一定程度上有去噪的效果。
PCA另一个重要特性是能将数据变换为元素之间彼此不想关的表示，可以消除数据中未知变化因素。所以PCA也是一种数据白化的技术。
由 $z^{(i)}=W^Tx^{(i)}$ 可知，高维空间到低维空间的函数映射是线性的，但是在许多现实任务中，可能需要非线性映射才能找到恰当的低维嵌入。这时我们可以用SVM中提到的核技巧来引入非线性。