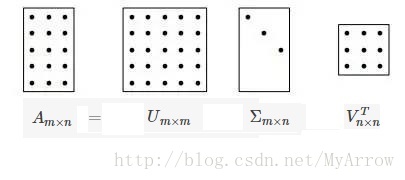
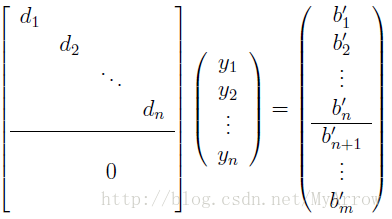SVD原理
SVD定义
1、对于方阵,我们可以将其特征分解为:
A=X∧X−1A=X∧X−1
- X的列:为A的特征向量
- ∧为对角矩阵:对角线上的值为A的特征值,按从大到小的顺序排列
2、对于普通矩阵,其总可以进行奇异值分解:
A=UΣ
- 其中U 和V都为正交矩阵,Σ为对角矩阵
- 几何含义:
表示找到了U和V这样两组基:A矩阵的作用是将一个向量从V这组正交基向量的空间旋转到U这组正交基向量的空间,并对每 个方向进行了一定的缩放(由Σ决定),缩放因子就是各个奇异值。如果V的维度比U 大,则表示还进行了投影。
奇异值分解:将一个矩阵原本混合在一起的三种作用效果,分解出来了。
SVD的分解示意图如下:
SVD性质
- 奇异值的比例不变性:
即αA的奇异值是A的奇异值的|α|倍
- 奇异值的旋转不变性:
若P是正交矩阵且detA=1(即P为旋转矩阵),PA的奇异值与A的奇异值相同
奇异值的比例和旋转不变性:在数字图像的旋转、镜像、平移、放大、缩小等几何变换方面有很好的应用
- 容易得到矩阵A的秩为k(k≤r)的一个最佳逼近矩阵
用于PCA降维
解线性方程组
解非齐次线性方程组
求解非齐次线性方程组Ax = b,以下我们只讨论超定方程的情况,即方程个数多于未知遍历的个数。
- 等价于寻找x使||Ax−b||
最小化 (向量2范数,转化为最优化问题)
1)对A进行SVD分解,,则优化问题变为
![]()
2)我们令
![]()
则优化问题变为:
![]()
3)求解向量y:
当Dy−b′=0时,上述最优化问题可以取得最小值,其用方程组可以表示如下:
则:
![]()
4)求解向量x:
x = Vy
解齐次线性方程组
对于齐次线性方程组,可以将问题转化为||Ax||的优化问题,为了避免x = 0这种特解,我们增加一个约束,如||x||
=1,这样,问题便成了:

由于D是一个对角矩阵,对角元素按降序排列,因此最优解在时取得,又因为x = Vy,所以最优解就是V的最小奇异值对应的列向量,即V的最后一列。
PCA降维
待续。
参考链接: