版权声明:转载请注明出处。 https://blog.csdn.net/baidu_38304645/article/details/83714526
在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。
用4种不同形态的L型骨牌, 覆盖给定特殊棋盘上除特殊方格以外的所有方格,且任何2个不得重叠。

输入:特殊方格的位置(0-size-1),方格的大小size
输出:各个方格所属的骨牌的编号,骨牌的编号由放置的顺序决定,越早放编号越小。特殊方格由-1表示。
运行结果:
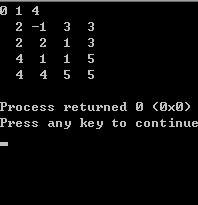
当k>0时,将棋盘分割成 4 个
子棋盘
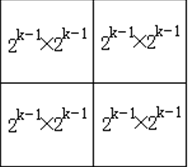
特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。
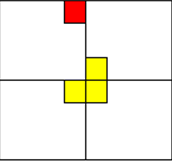
为将无特殊方格子棋盘转化为特殊棋盘,可以用一个骨牌覆盖3个较小棋盘的回合处,从而将原问题转化为3个较小规模的棋盘覆盖问题。
递归地使用这种分割,直至棋盘简化为棋盘 1 * 1。
int board[10][10]; //棋盘 (0,0)表示左上角
int tile; //L型骨牌的编号
//棋盘左上角的行号,列号,特殊方格所在的行号,列号,棋盘的大小
void chessbord(int tr, int tc, int dr, int dc, int size)
{
int t, s;
if(size == 1)
return;
s = size / 2; //分割棋盘
t = tile++; //L型骨牌号
//覆盖左上角子棋盘
if(dr<tr+s && dc<tc+s)
chessbord(tr, tc, dr, dc, s); //特殊方格在此棋盘中
else
{
//此棋盘中无特殊方格,用t号L型骨牌覆盖右下角
board[tr+s-1][tc+s-1] = t;
//覆盖其余方格
chessbord(tr, tc, tr+s-1, tc+s-1, s);
}
if(dr<tr+s && dc>=tc+s)
chessbord(tr, tc+s, dr, dc, s);
else
{
//此棋盘中无特殊方格,用t号L型骨牌覆盖左下角
board[tr+s-1][tc+s] = t;
chessbord(tr, tc+s, tr+s-1, tc+s, s);
}
if(dr>=tr+s && dc<tc+s)
chessbord(tr+s, tc, dr, dc, s);
else
{
//此棋盘中无特殊方格,用t号L型骨牌覆盖右上角
board[tr+s][tc+s-1] = t;
chessbord(tr+s, tc, tr+s, tc+s-1, s);
}
if(dr>=tr+s && dc>=tc+s)
chessbord(tr+s, tc+s, dr, dc, s);
else
{
//此棋盘中无特殊方格,用t号L型骨牌覆盖左上角
board[tr+s][tc+s] = t;
chessbord(tr+s, tc+s, tr+s, tc+s, s);
}
}复杂度分析:
T(k) =
O(1) k=0
4T(k-1) + O(1) k>0
渐进意义上的最佳算法
推导过程: 原式等价于 T(k)=4T(k-1)+1
递推得: 4T(k-1)=4(4T(k-2)+1)=42T(k-2)+4
T(k)= 42T(k-2)+4 +1
又有: 42T(k-2)=43T(k-3)+42
故 T(k)= 43T(k-3)+42+4+1
………………….
T(k)=4kT(0)+4k-1+…+4+1=O(4k)