常见的机器学习&数据挖掘知识点之Basis

版权声明：未经许可, 不能转载 https://blog.csdn.net/heyongluoyao8/article/details/47852057

常见的机器学习&数据挖掘知识点之Basis

• SSE(Sum of Squared Error, 平方误差和)
  $$SSE=\sum_{i=1}^{n}(X_i-\overline{X})^2$$
• SAE(Sum of Absolute Error, 绝对误差和)
  $$SAE=\sum_{i=1}^{n}|X_i-\overline{X}|$$
• SRE(Sum of Relative Error, 相对误差和)
  $$SRE＝\sum_{i=1}^{n}{\frac{X_i-\overline{X}}{\overline{X}}}$$
• MSE(Mean Squared Error, 均方误差)
  $$MSE=\frac{\sum_{i=1}^{n}(X_{i}-\overline{X})^2}{n}$$
• RMSE(Root Mean Squared Error, 均方根误差)，又称SD(Standard Deviation, 标准差)
  $$RMSE=\sqrt{\frac{\sum_{i=1}^{n}(X_{i}-\overline{X})^2}{n}}$$
• MAE(Mean Absolute Error, 平均绝对误差)
  $$MAE=\frac{\sum_{i=1}^{n}|X_i-\overline{X}|}{n}$$
• RAE(Root Absolute Error, 平均绝对误差平方根)
  $$RAE=\sqrt{\frac{\sum_{i=1}^{n}|X_i-\overline{X}|}{n}}$$
• MRSE(Mean Relative Square Error, 相对平均误差)
  $$MRSE＝\frac{\sum_{i=1}^{n}{\frac{X_i-\overline{X}}{\overline{X}}}}{n}$$
• RRSE(Root Relative Squared Error, 相对平方根误差)
  $$RRSE＝\sqrt{\frac{\sum_{i=1}^{n}{\frac{X_i-\overline{X}}{\overline{X}}}}{n}}$$
• Expectation(期望)&Variance(方差)
    期望是描述一个随机变量的“期望值”，方差反映着随机变量偏离期望的程度，偏离程度越大哦，方差越大，反之则相反。对于离散随机变量$X$，其期望为：
  $$E(X)=\sum_{i=1}^{\infty}x_ip(x_i)$$
    其中$p(x)$为随机变量的$X$的分布率(概率分布).
    其方差为：
  $$D(X)=\sum_{i=1}^{\infty}[x_i-E(X)]^2p(x_i)$$
    对于连续变量$X$，其期望为：
  $$E(X)=\int_{-\infty}^{+\infty}xf(x)dx$$
    其中$f(x)$为随机变量的$X$的概率密度分布.
    其方差为：
  $$D(X)=\int_{-\infty}^{+\infty}[x-E(X)]^2f(x)dx$$
    对于$Y＝g(X)$($g$是连续函数)，则$Y$的期望为：
    $X$是离散随机变量：
  $$E(Y)=E(g(x))=\sum_{i=1}^{\infty}g(x_i)p(x_i)$$
    $X$是连续随机变量：
  $$E(Y)=E(g(x))=\int_{-\infty}^{+\infty}g(x_i)f(x)dx$$
    常见分布的期望与方差：

分布/数字特征	期望	方差
两点分布	$q$	$pq$
二项分布	$np$	$npq$
泊松分布	$\lambda$	$\lambda$
均匀分布	$\frac{a+b}{2}$	$\frac{1}{12}(b-a)^2$
指数分布	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$
正态分布	$\mu$	$\sigma^2$

 

• 标准差：
    标准差为方差的平方根，即：
  $$V(X)=\sqrt {D(X)}$$
• JP(Joint Probability, 联合概率)
  
  • 二维离散随机变量$X$, $Y$
    
    • 联合概率分布(分布率)
      $$P(x,y)=P\{X=x_i,Y=y_i\}=p_{ij}$$
      $$p_{ij} \geq 0$$
      $$\sum_{ij}p_{ij}=\sum_i \sum_j p_{ij}=1$$
    • 联合分布函数
      $$F(x,y)=P\{X \leq x, Y \leq y\}=\sum^x \sum^y P(x,y)$$
  • 二维连续随机变量$X$, $Y$
    
    • 联合概率密度
      $$f(x,y)$$
    • 联合分布函数
      $$F(x,y)=\int_{-\infty}^{x} \int_{-\infty}^{y} f(u,v)dudv$$
      $$f(x,y) \geq 0$$
      $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}f(x,y)dxdy=F(+\infty,+\infty)=1$$
• MP(Marginal Probability, 边缘概率)
  
  • 二维离散随机变量
    
    • X的边缘分布率
      $$p_{i.}=P\{X=x_i\}=\sum_{j=1}^{\infty}p_{ij}, j=1,2,3,...$$
    • Y的边缘分布率
      $$p_{.j}=P\{Y=y_i\}=\sum_{i=1}^{\infty}p_{ij}, i=1,2,3,...$$
    • X的边缘分布函数
      $$F_{X}(x)=F(x,+\infty)=P\{X \leq x\}=P\{X \leq x,Y \leq +\infty\}$$
    • Y的边缘分布函数
      $$F_{Y}(y)=F(+\infty,y)=P\{Y \leq y\}=P\{X \leq +\infty, Y \leq y\}$$
  • 二维连续随机变量
    
    • X的边缘分布率
      $$f_{X}(x)=\int_{-\infty}^{+\infty}f(x,y)dy$$
    • Y的边缘分布率
      $$f_{Y}(y)=\int_{-\infty}^{+\infty}f(x,y)dx$$
    • X的边缘分布函数
      $$F_{X}(x)=F(x,+\infty)=\int_{-\infty}^{x}[\int_{-\infty}^{+\infty}f(u,y)dy]du$$
    • Y的边缘分布函数
      $$F_{Y}(y)=F(y,+\infty)=\int_{-\infty}^{y}[\int_{-\infty}^{+\infty}f(x,v)dx]dv$$
• Independence(独立性)
    若对一切$x$, $y$，都有：
  $$P\{X \leq x, Y \leq y\}=P\{X \leq x\}P\{Y \leq y\}$$
    即：
  $$F(x,y)=F_X(x)F_Y(y)$$
  则随机变量X, Y是互相独立的.
    对于离散随机变量，等价于：
  $$P\{X=x_i, Y=y_j\}=P\{X=x_i\}P\{Y=y_j\}, i,j=1,2,...$$
    对于连续随机变量，等价于：
  $$f(x,y)=f_x(x)f_y(y)$$
• CP(Conditional Probability, 条件概率)
    对于离散随机变量，定义为:
  若$P\{Y=y_j\} >0$：
  $$P\{X=x_i|Y=y_j\}=\frac{P\{X=x_i, Y=y_j\}}{P\{Y=y_j\}}=\frac{p_{ij}}{p_{.j}}, i=1,2,...$$
    而 $$P\{Y=y_j\}=p_{.j}=\sum_{i=1}^{\infty}p_{ij}$$
    因此：
  $$P\{X=x_i|Y=y_j\}=\frac{P\{X=x_i, Y=y_j\}}{P\{Y=y_j\}}=\frac{p_{ij}}{\sum_{i=1}^{\infty}p_{ij}}, i=1,2,...$$
    上式即为在$Y=y_j$条件下$X$的条件分布律.
    同理：
  $$P\{Y=y_j|X=x_i\}=\frac{P\{X=x_i, Y=y_j\}}{P\{X=x_i\}}=\frac{p_{ij}}{\sum_{j=1}^{\infty}p_{ij}}, j=1,2,...$$
    上式即为在$X=x_i$条件下$Y$的条件分布律.
    对于连续随机变量，定义为:
  $$F_{X|Y}(x|y)=P\{X \leq x|Y =y\}=\frac{\int_{-\infty}^{x}f(x,y)dx}{f_Y(y)}$$
  $$F_{Y|X}(y|x)=P\{Y \leq y|X = x\}=\frac{\int_{-\infty}^{y}f(x,y)dy}{f_X(x)}$$
    条件概率密度分别为：
  $$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$$
  $$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}$$
• Bayesian Formula(贝叶斯公式)
    使用已知知识来对先验概率进行修正，得到后验概率，即得到条件概率：
  $$P(B_i||A)=\frac{P(B_i)P(A|B_i)}{\sum_{i=1}^{n}P(B_i)P(A|B_i)}$$
    $P(B_i||A)$为后验概率，$P(B_i|)$为先验概率.
• CC(Correlation Coefficient, 相关系数)
    对于$(X,Y)$为二维随机变量，若$E\{[X-E(X)][Y-E(Y)]\}$存在，则称它为随机变量$X$与$Y$的协方差，记为$cov(X,Y)$或$\sigma_{XY}$，即：
  $$cov(X,Y))=E\{[X-E(X)][Y-E(Y)]\}$$
    当$D(X)>0, D(Y)>0$时，
  $$\rho_{XY}=\frac{cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$$
  称为随机变量$X,Y$的相关系数或标准协方差.
    特别地，
  $$cov(X,X)=D(X)$$
  $$cov(Y,Y)=D(Y)$$
  因此方差是协方差的特例.
    若$X,Y$相互独立，则$cov(X,Y)=0$，从而$\rho_{XY}=0$. 同时$|\rho_{XY}| \leq 1$. 若$|\rho_{XY}| ＝ 1$，则随机变量$X,Y$线性相关. $+1$代表正线性相关，$-1$代表负线性相关，绝对值越大则表明它们之间越相关，若为0，则表示它们互相独立.
• Covariance(协方差矩阵)
    若$X$是由随机变量组成的$n$列向量，$E(X_i)=\mu_i$，那么协方差矩阵定义如下：
  $$\begin{equation} %开始数学环境 \Sigma=\left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 E\{[X_1-E(X_1)][X_1-E(X_1)]\} &... &E\{[X_1-E(X_1)][X_n-E(X_n)]\} \\ %第一行元素 ... & ... & ...\\ %第二行元素 E\{[X_n-E(X_n)][X_1-E(X_1)]\} &... &E\{[X_n-E(X_n)][X_n-E(X_n)]\} \\ %第一行元素 \end{array} \right] = %右括号 \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 E\{[X_1-\mu_1][X_1-\mu_1]\} &... &E\{[X_1-\mu_1][X_n-\mu_n]\} \\ %第一行元素 .. & ... & ...\\ %第二行元素 E\{[X_n-\mu_n][X_1-\mu_1]\} &... &E\{[X_n-\mu_n][X_n-\mu_n]\} \\ %第一行元素 \end{array} \right] \end{equation}$$
• Quantile (分位数)
    对随机变量$X$，其分布函数为$F(x)$，任意给定$\alpha, 0<\alpha<1$，$P(X<=x)=F(x)=\alpha$所对应的x，为$\alpha$分位数.

---

• LMS(Least Mean Squared, 最小均方)
    优化的目标为使得均方误差最小，参数即为最小时所对应的参数值，即:
  $$\theta=argmin_{\theta}{\frac{1}{2}}\frac{\sum_{i=1}^{n}(X_i-\overline{X})^2}{n}=argmin_{\theta}{\frac{1}{2}}\sum_{i=1}^{n}(X_i-\overline{X})^2$$
    公式中的$\frac{1}{2}$为了在求导过程中的方便，因为平方项在求导过程中会产生一个2倍，这样便能约掉常数项，目标函数乘以一个常数对结果是没有影响的，只是目标值缩小了一半，但是其所对应的参数还是不变的。可以使用梯度下降法来进行求解。
• LSM(Least Square Methods, 最小二乘法)
    在最小二乘法中使用最小均方来对参数进行求解，对于样本点集$(X,Y)=\{(X^1,y^1),...,(X^n,y^n)\}$，其中每个样本特征向量为$X^i=\{x_1^i,...,x_m^i\}$，$n$为样本个数，$m$为样本点的维度，那么其线性回归方程：
  $$f(X^i)=w_0+w_1x_1^i+w_2x_2^i+...+w_mx_m^i=W^T[1,{X^i}^T]^T, i\in[1,n]$$
    那么，优化目标为：
  $$min F = min\frac{1}{2}\sum_{i=1}^{n}(f(X^i)-y^i)^2$$
    为了书写方便，将常数1作为每个样本特征向量的第1个分量，即$X^i=\{1,x_1^i,...,x_m^i\}$，那么线性回归方程变为：
  $$f(X^i)=W^TX^i, i\in[1,n]$$
    那么优化目标为：
  $$min F = min\frac{1}{2}\sum_{i=1}^{n}(W^TX^i-y^i)^2$$
• GD(Gradient Descent, 梯度下降)
    对于最小二乘法中的F最小化求解使用梯度下降算法进行求解（如果是求解最大值，则使用梯度上升算法），梯度下降算法即为从某个初始点出发，按照梯度下降的方向，每次前进一步，直到最小值点，因此需要一个步长$\alpha$。
  
  1. 首先求取梯度
     $$\nabla_{w}J(w) =\sum_{i=1}^{n}(W^TX^i-y^i)X^i=X^T(XW^T-\overrightarrow y)$$
       那么前进方向为$g=-\nabla_{w}J(w)$，即梯度的反方向, 如果是梯度上升算法，那么就是梯度方向，则不需要在前面加上负号.
  2. 然后按照梯度方向进行前进
     $$W:=W+\alpha g$$
       其中$\alpha>0$，它是一个步长，对于$\alpha$具体取多大的值，一般按照经验进行取，可以从10, 1,0.1,0.01,0.001不断进行尝试而取一个合理的值。而可以刚开始取一个较大值，后面越来越小，这样刚开始步子就大一点，到逐渐接近最优点的时候，放慢脚步，如果这时候过大，就会造成一直在最优点附近震荡。
  3. 最后，按照步骤2进行迭代更新$W$，直到目标函数值不再变化，或者变化的范围小于事先设定的阈值。所以，梯度下降算法的一个缺点就是需要确定$\alpha$的值，但是该值并不好确定，需要不断进行尝试和依靠经验。
• SGD(Stochastic Gradient Descent, 随机梯度下降)
     在梯度下降法中，参数的每一次更新都要使用训练集中的全部的样本(批量梯度下降算法)，这样速度便相对较慢，于是每次更新时随机选择一个样本进行更新参数，这样便能提高计算速度，但每次更新的方向并不一定朝着全局最优化方向.
• 正规方程求解方法
     该方法利用极值点的偏导数为0，即令：
  $$\nabla_{W}J(W) = X^TXW^T-X^T\overrightarrow y=0$$
    得到正规方程：
  $$X^TXW=X^T\overrightarrow y$$
    求解$W$：
  $$W=(X^TX)^{-1}X^T\overrightarrow y$$
    该方法的时间复杂度为$O(n^3)$，因为需要对矩阵求逆运算，其中$n$为$(X^TX)^{-1}$的特征数量，如果$n$值很大，那么求解速度将会很慢。对此，Andrew Ng的经验建议是：如果$n>10000$，那么使用梯度下降算法进行求解。同时，如果$(X^TX)$是奇异矩阵，即含有0特征值，那么其便不可逆，一个解决方法便是L2正则，后面将会讲到。
• MLE(Maximum Likelihood Estimation, 极大似然估计)
    在我们已经知道到随机变量的一系列观察值，即试验结果已知(样本)，而需要求得满足该样本分布的参数$\theta$，于是我们需要采取某种方法对$\theta$进行估计，在最大似然估计中，我们假定观察的样本是该样本分布下中最大可能出现的，把最大可能性所对应的参数$\theta$对真实的$\theta^*$进行参数估计。
  
  • 对于离散随机变量
      设总体$X$是离散随机变量，其概率分布$P(x;\theta)$(注意：与$P(x,\theta)$的区别，前者中$\theta$是一个常数，只是值暂时不知道，也就是它是一个确定值，而后者中$\theta$是一个随机变量)，其中$\theta$是未知参数. 设$X_1,X_2,...,X_n$分别都是取自总体$X$的样本，我们通过试验观察到各样本的取值分别是$x_1,x_2,...,x_n$，则该事件发生的概率，即它们的联合概率为：
    $$P(X_1=x_1,X_2=x_2,...,X_n=x_n)$$
      假设它们独立同分布，那么联合概率为：
    $$P(X_1=x_1,X_2=x_2,...,X_n=x_n)=\prod_{i=1}^{n}P(x_i;\theta)$$
    因为$x_i, i \in \{1,2,...,n\}$都是已知的确定的值，那么上式的值取决于$\theta$，从直观上来说，一件已经发生的事件，那么该事件发生概率应该较大，我们假设该事件的发生概率是最大的，即$x_1,x_2,...,x_n$的出现具有最大的概率，在这种假设下去求取$\theta$值.
      定义似然函数为：
    $$\ell(\theta)=\ell(x_1,x_2,...,x_n;\theta)=\prod_{i=1}^{n}P(x_i;\theta)$$
    它是关于$\theta$的函数.
      极大似然估计法就是在参数$\theta$的取值范围$\Theta$内选取一个使得$\ell(\theta)$达到最大值所对应的参数$\hat{\theta}$，用来作为$\theta$的真实值$\theta^*$的估计值，即：
    $\theta=argmax_{\theta \in \Theta}\ell(x_1,x_2,...,x_n;\theta)$
      这样，对求解总体$X$的参数$\theta$极大似然估计问题转化为求似然函数$\ell(\theta)$的最大值为题，那么求去最大值问题可以使用导函数进行求解.
      为了便于求解，对似然函数进行$ln$运算，因为$ln$为递增函数，那么$ln(\ell(\theta))$与$\ell(\theta)$在同一处取得最大值，于是,
    $$ln \ell(\theta)=ln \prod_{i=1}^{n}P(x_i;\theta)=\sum_{i=1}^{n}ln P(x_i;\theta)$$
      对上式进行求导操作，并令导函数为0:
    $$\frac{d ln \ell(\theta)}{d\theta}=0$$
    解该方程，得到$\theta$作为真实值的估计.
  • 对于连续离散随机变量：
      设总体$X$是连续随机变量，其概率密度函数为$f(x;\theta)$，对样本$X_1,X_2,...,X_n$观察得到的样本值分别为$x_1,x_2,...,x_n$，那么联合密度函数为：
    $$\prod_{i=1}^{n}f(x_i;\theta)$$
    则，似然函数为：
    $$\ell(\theta)=\prod_{i=1}^{n}f(x_i;\theta)$$
      同理，按照先前的处理与求解方式，即极大似然估计法，求取theta值.
      前面所说的使用已知知识对先验概率进行矫正，得到后验概率，便可以用到似然函数，即后验概率＝先验概率＊似然函数.
  • 极大似然估计步骤：
    
    1. 由总体分布导出样本的联合概率函数(或联合密度)；
    2. 把样本联合概率函数(或联合密度)中自变量看成为已知数，而参数$\theta$作为自变量未知数，得到似然函数$\ell(\theta)$；
    3. 将似然函数转化为对数似然函数，然后求取对数似然函数的最大值，一般使用求导方法；
    4. 最后得到最大值表达式，用样本值代入得到参数的极大似然估计值.
• QP(Quadratic Programming, 二次规划)
    我们经常用到线性规划去求解一部分问题，然后很多问题是非线性的，而二次规划是最简单的非线性规划，简称QP问题，何为二次规划，即其目标函数是二次函数，而约束条件是线性约束的最优化问题. 用数学语言描述，其标准形式为：
  $$min f(x)=\frac{1}{2}x^TGx+g^Tx$$
  $$s.t. a_i^Tx=b_i, i \in E\\ a_j^Tx \geq b_j, j \in I$$
  其中，$G$是$n \times n$的对称矩阵(Hessian矩阵)，$E,I$分别对应等式约束和不等式约束指标集合，$g,x,\{a_i|i \in E\}, \{a_j|j \in I\}$都是$n$维列向量
  
  • 若G正半定，那么QP问题存在全局最优解(凸二次规划)；
  • 若G正定，那么QP问题存在唯一的全局最优价(凸二次规划)；
  • 若G不定，那么可能存在非全局的最优解；
    凸二次规划即二次规划目标函为维凸函数.
• L1 /L2 Regularization(L1/L2正则)
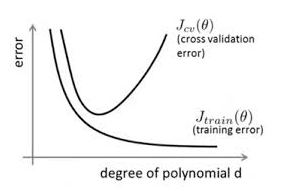
    我们在做数据挖掘或机器学些的时候，在训练数据不够时，或者出现过度训练时，往往容易过拟合，即训练时效果特别好，而测试时或者在新数据来临时，模型效果较差，即为模型的泛化能力比较差。随着训练过程不断进行，该模型在training data上的error渐渐减小，但是在验证集上的error却反而渐渐增大——因为训练出来的网络过拟合了训练集，对训练集外的数据(测试数据或者新数据)却不work。如下图所示：
    避免过拟合的方法有很多：early stopping, 数据集扩增(Data augmentation), 正则化(Regularization),Dropout等.
  
  • L1
      L1正则是一个稀疏规则算子，其是在代价函数(优化目标函数)后面加上参数$w$绝对值和乘以$\frac{\lambda}{n}$，目标函数即为：
    $$F=F_0+\frac{\lambda}{n}\sum_w|w|$$
    其中$F_0$为原目标函数，那么新目标函数的导数为：
    $$\frac{\partial F}{\partial w}=\frac{\partial F_0}{\partial w}+\frac{\lambda}{n}sgn(w)$$
    上式中$sgn(w)$是$w$的符号函数，$\alpha>0$是更新步长，它是一个常数，$\lambda>0$是正则项数，它是一个常数，那么参数$w$的梯度下降算法更新方程为：
    $$w:=w-\alpha\frac{\partial F_0}{\partial w}-\alpha\frac{\lambda}{n}sgn(w)$$
    上面的更新方程比原来的多了$\alpha\frac{\lambda}{n}sgn(w)$这一项. 当$w$为正时，更新后$w$变小，为负时则相反，即将$w$往0值靠，这样对于那些接近0值的参数，那么就可能为0，这样很多$w$就会趋近于0，这样便起到了稀疏作用，也就是为何叫做”稀疏规则算子”了，这样相当于降低了模型的复杂度，提高模型泛化能力，防止过拟合.
      任何正则化算子，如果它在等于0处不可微，并且可以分解为一个“求和”的形式，那么这个正则化算子就可以实现稀疏. 也就是这么说，$w$的L1范数正则是绝对值，而|w|在w=0处是不可微. 其实L0范数正则(L0范数是指向量中非0的元素的个数)，也可以达到稀疏目的，但是现实中为什么不用L0正则呢，因为L0范数正则的优化是一个NP难问题，所以L1范数正则具有更好的优化特性.
      在$w$的更新式子中，当$w$为0时，$|w|$是不可导的，所以需要按照原始的未经正则化的方法去更新$w$，即为了方便我们定义$sgn(0)=0$，这样便统一了所有情况.
      L1正则的稀疏性特性可能用来进行特征选择，只选择那些重要的，区分能力强的特征，而去掉那些不重要的，区分能力不强的特征. 虽然如果加上这些特征，可能会使得在模型训练时效果更好，但是可能会造成过拟合，从而模型的泛化能力不强.
      在线性回归中使用L1正则的叫做LASSO(Least Absolute Shrinkage and Selectionator Operator L1正则最小二乘回归).
  • L2
      L2范数正则化是在代价函数(优化目标函数)后面加上平方和正则项，即：
    $$F=F_0+\frac{\lambda}{2n}\sum_w w^2$$
    注意：常数项的$w$是不带入正则项中的，为了便于区分，将其用b表示.
    其中$F_0$为原始目标函数，在正则项前面乘以$\frac{1}{2}$是为了在求导过程中方便，因为平方项在求导过程中会产生一个2倍，这样便能约掉常数项. 那么新目标函数的导数为：
    $$\frac{\partial F}{\partial w}=\frac{\partial F_0}{\partial w}+\frac{\lambda}{n}w\\\frac{\partial F}{\partial b}=\frac{\partial F_0}{\partial b}$$
      这样参数的更新方程为:
    $$w:=w-\alpha \frac{\partial F_0}{\partial w}-\alpha \frac{\lambda}{n}w=(1-\alpha \frac{\lambda}{n})w-\alpha \frac{\partial F_0}{\partial w}\\ b:=b-\alpha \frac{\partial F_0}{\partial b}$$
    其中，$\alpha>0$是更新步长，它是一个常数，$\lambda>0$是正则项数，它是一个常数
      从$w$更新方程中可以看出，在不使用L2正则项时，求导结果中的$w$前的系数为1，而现在前面的系数为$(1-\alpha \frac{\lambda}{n})$，因为$\alpha, \lambda, n$都是正数，因此前面的系数小于0，它的效果就是减小$w$，这就是为何L2正则又被称为“权值衰减”(weight decay).
      通过L2正则来降低模型的复杂度，提高模型的泛化能力，防止过拟合，并且L2正则本书是一个凸二次函数，这样便有利于优化.
      在前面所说的正规方程中，若$X^TX$不可逆，则无法进行求解，那么如果加上L2正则项，就变成：
    $$W=(X^TX+\lambda I)^{-1}X^T\overrightarrow y$$
    这样$(X^TX+\lambda I)$肯定是可逆的.
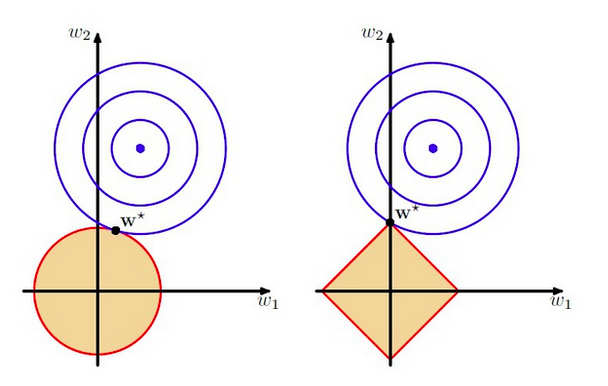
      最后通过一张图直观上来区别L1与L2正则，如图:
    
    $$From PRML$$
      上图中使用的模型是线性回归，该模型中有两个特征，要优化的参数分别是w1和w2，左图的正则化是L2，右图是L1. 蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值(假设一个样本)，半径就是误差值，受限条件就是红色边界(就是正则化那部分)，二者相交处，才是最优参数. 可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏.
      从另一个角度上来看，正则化其实就是对模型的参数设定一个先验，这是贝叶斯学派的观点，也是一种理解。L1正则是Laplace先验，L2是高斯先验.
  • L2.5
      该正则化集合了L1与L2正则，具有它们两者的优点.
• Eigenvalue(特征值)&Eigenvector(特征向量)
    设$A$是$n$阶矩阵，如果数$lambda$和n维非零列向量$\alpha$，使得：
  $$A\alpha=\lambda\alpha$$
  成立，则称这样的数$\lambda$为方阵$A$的特征值，非零列向量$\alpha$称为$A$对应于特征值$\lambda$的特征向量.
    特征向量$\alpha \ne 0$，特征值$\lambda$都是对方阵来说的；
    $n$阶方阵$A$的特征值即为使得
  齐次线性方程组$(\lambda I-A)x=0$有非零解的$\lambda$值，即满足方程$|\lambda I-A|=0$的$\lambda$都是矩阵$A$的特征值.
    特征值积等于方阵的行列式值，即： $$\prod_{i=1}^{n}\lambda_i=|A|$$
    若特征值$\lambda_i$互不相等，那么它们所对应的特征向量$\alpha_i$线性不相关.
    若方阵的行列式值为0，即为奇异方阵，也即其含有为0的特征值，那么该方阵不可逆.