常见的机器学习与数据挖掘知识点之常见分布

版权声明：未经许可, 不能转载 https://blog.csdn.net/heyongluoyao8/article/details/47982443

常见的机器学习与数据挖掘知识点之常见分布

Common Distribution(常见分布)：

Discrete Distribution(离散型分布)：

• 0-1 Distribution(0-1分布)
  定义：若随机变量$X$只取$0$和$1$两个值，且其分布律为
  $$P\{X=k\}=p^k(1-p)^{1-k}, k=0,1$$
  其中$X$服从参数为p的$(0-1)$分布，记作$X \sim (0-1)$. 如抛掷硬币一次便服从两点分布.
    两点分布的期望与方差分别为：$p, 1-p$.
• Geometric Distribution(几何分布)
  定义：若随机变量$X$的可能取值为$1,2,3,...$且它的分布律为
  $$P\{X=k\}=(1-p)^{k-1}p=q^{k-1}p, k=1,2,3,...$$
  则称随机变量$X$服从参数p的几何分布，记作$X \sim G(p)$.
    几何分布具有无记忆性，即：
  $$P\{X>m+n|X>m\}=P\{X>n\}$$
  指几何分布对过去的m次失败的信息在后面的计算中被遗忘了.
    几何分布对应于：$X$为独立重复的贝努利试验这种，“首次成功”时的试验次数.
    几何分布的期望与方差分别为：$\frac{1}{p}, \frac{1-p}{p^2}$.
• Hypergeometric Distribution(超几何分布)
  定义：若随机变量$X$的可能取值为$0,1,2,....,n$，而且其分布律为
  $$P\{X=m\}=\frac{C_M^mC_{N-M}^{n-m}}{C_{N}^{n}}$$
  其中$n,M,N$都是正整数，且$n \leq N, M \leq N$. 上式中当$m>M$或$n-m>N-M$时，显然有$P{X=m}=0$，称这种分布为超几何分布，记作$X \sim H(n,M,N)$.
    超几何分布对应与不返回抽样模型：$N$个产品中有$M$个不合格产品，从中抽取$n$个，那么不合格的产品个数为$X$.
    超几何分布的期望与方差分别为：$\frac{nM}{N}, \frac{nM}{N}\frac{N-M}{N}\frac{N-n}{N-1}$.
• Bernoulli Distribution/Binomial Distribution(贝努利分布/二项分布)
  定义：设随机变量$X$的可能取值为$0,1,2,...,n$，其它的分布律为
  $$P\{X=k\}=C_n^kp^k(1-p)^{n-k}$$
  则称随机变量$X$服从参数为$n,p$的二项分布，记作$X \sim B(n,p)$，它是$n$重独立贝努利试验分布成功$k$次，当$n=1$时，其退化成$0-1$分布.
    设随机变量$X \sim H(n,M,N)$，则当$N \to \infty$时，$X$近似地服从二项分布$B(n,p)$，即下面的近似等式成立.
    二项分布的期望与方差分别为：$np, np(1-p)$.
• Negative Binomial Distribution(负二项分布，又称Pascal 帕斯卡分布)
  定义：若随机变量$X$的可能取值为$r,r+1,...$，而且其分布律为
  $$P\{X=k\}=C_{k-1}^{r-1}(1-p)^{k-r}p^r, k=r,r+1,...$$
  其中,$r, p$都是常数，那么称随机变量$X$服从参数$r,p$的负二项分布，记作$X \sim NB(r,p)$.
    负二项分布是：X为独立重复的贝努利试验中，“第$r$次成功“时的试验次数.
    负二项分布的期望与方差分别为：$\frac{r}{p}, \frac{r(1-p)}{p^2}$.
    二项随机变量时独立$0-1$随机变量之和.
    在n重贝努利试验可看作由$n$个相同的，独立进行的贝努利试验组成，若将第$i$个贝努利试验中成功的次数记为$X_i \sim B(1,p), i=1,...,n$，$n$重贝努利试验成功的总次数$X=X_1+X_2+...+X_n$，它服从$B(n,p)$.
    负二项随机变量时独立几何随机变量之和.
    做一系列的贝努利试验，如果将首个成功出现的试验次数记为$X_1$，第二个成功出现时的试验次数(从第一次成功之后算起)记为$X_2$，……，第$r$个成功出现时的试验次数记为$X_r$，则$X_i$独立同分布，且$X_i \sim G(p)$. 此时有$X=X_1+X_2+...+X_n \sim NB(r,p)$.
• Multinomial Distribution(多项分布)
  定义:：若$m$维随机变量$(X_1,X_2,...,X_m)$可能取值为$(k_1,K_2,...,K_m)$，而且其分布律为
  $$P\{X_1=k_1,X_2=k_2,...,X_m=k_m\}=\frac{n!}{k_1!k_2!...k_m!}p_1^{k_1}p_2^{k_2}...p_m^{k_m}$$
  其中，$\sum_{i=1}^m k_i=n$，$p_i$>0为试验结果是$x_i$的概率，$k_i$表示试验结果是$x_i$的次数. 那么称随机变量$(X_1,X_2,...,X_m)$服从多项分布，记作$(X_1,X_2,...,X_m) \sim M(n, p_1, p_2,...,p_m)$.
    通俗地说，假设一次随机试验取值范围可能为${x_1,x_2,...x_m}$，每个出现的概率依次为$p_1,p_2,...,p_m$，现进行独立重复$n$次试验，分别将它们的出现次数记为随机变量$X_1,X_2,...,X_m$，那么该试验就是一个多项分布试验.
    多项分布的所有期望与协方差矩阵分别为：$E=(np_1,np_2,...,np_m), COV_{m \times m}=(c_{ij}), 其中c_{ii}=np_iq_i, c_{ij}=-np_ip_j(i \ne j)$.
• Poisson Distribution (泊松分布)
  定义：若随机变量$X$的可能取值为$0,1,2,...$，其分布律为
  $$P\{X=k\}=\frac{\lambda ^k}{k!}e^{-\lambda}, k=0,1,2,...; 常数\lambda>0$$
  则称随机变量$X$服从参数为$\lambda$的泊松分布，记作$X \sim P(\lambda)$.
    泊松定理：设随机变量$X_n \sim B(n,p_n), n=1,2,3,...; p_n$是与$n$无关的数$)$. 又设$np_n=\lambda>0, n=1,2,...$是常数，则有
  $$lim_{n \to \infty}P\{X_n=k\}=\frac{\lambda_k}{k!}e^{-\lambda}$$
    当$np_n=\lambda$(常数)意味着当$n$很大时，$p_n$必定很小. 故当二项分布的$n$很大，$p$很小时，取$\lambda=np$，必有
  $$P\{X=k\}=C_n^kp^k(1-p)^{n-k}\approx\frac{\lambda^k}{k!}e^{-\lambda}$$
  在实际计算过程中，一般当$n \geq 10, p \leq 0.1$时可用$\frac{\lambda^k}{k!}e^{-\lambda}$作为$C_n^kp^k(1-p)^{n-k}$的近似值.
    泊松分布的期望与方差分别为：$\lambda, \lambda$.

Continuous Distribution (连续型分布)：

• Uniform Distribution(均匀分布)
  定义：设随机变量$X$的的概率密度为：
  $$\begin{equation} %开始数学环境 f(x)=\left\{ %左括号 \begin{array}{ccc} %该矩阵一共2列，每一列都居中放置 \frac{1}{b-a}, a \leq x \leq b, a \leq b \\ %第一行元素 0, others\\ %第二行元素 \end{array} \right] %右括号 \end{equation}$$
  则称随机变量$X$在区间$[a,b]$上服从均匀分布，记作$X \sim U[a,b]$.
    均匀分布的分布函数为：
  $$\begin{equation} %开始数学环境 F(x)=P\{X \leq x\}=\left\{ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 0, x \leq a\\%第一行元素 \frac{x-a}{b-a}, a \leq x \leq b, \\ %第二行元素 1, x \geq b\\ %第三行元素 \end{array} \right] %右括号 \end{equation}$$
    如果随机变量$X \sim U[a,b]$，那么落在$[a,b]$中任何子区间$[c,d](a \leq c \leq d \leq b)$内的概率为：
  $$P\{c\leq X \leq d\}=\int_c^d \frac{1}{b-a}dx=\frac{d-c}{b-a}$$
  这说明随机变量$X$落在子区间上的概率与子区间的长度成正比，而与该子区间的位置无关，即它落在$[a,b]$中任意一段相等长度的子区间内的可能性相同.
    均匀分布的期望与方差分别为：$\frac{a+b}{2}, \frac{(b-a)^2}{12}$.
    在实际中，服从均匀分布的例子很多，如：
  
  • 乘客候车时间服从均匀分布
  • 电台每隔20分钟发出一个信号，我们随手打开收音机，那么等待时间$t \sim [0,20]$
  • …..
• Exponential Distribution(指数分布)
  定义：若随机变量$X$的的概率密度为：
  $$\begin{equation} %开始数学环境 f(x)=\left\{ %左括号 \begin{array}{ccc} %该矩阵一共2列，每一列都居中放置 \lambda e^{-\lambda x}, x >0 \\ %第一行元素 0, x \leq0\\ %第二行元素 \end{array} \right] %右括号 \end{equation}$$
  其中$\lambda$是正常数，则称随机变量$X$服从参数为$\lambda$的指数分布，记作$X \sim E(\lambda)$.
  指数分布的分布函数为：
  $$\begin{equation} %开始数学环境 F(x)=\left\{ %左括号 \begin{array}{ccc} %该矩阵一共2列，每一列都居中放置 1-e^{-\lambda x}, x >0 \\ %第一行元素 0, x \leq0\\ %第二行元素 \end{array} \right] %右括号 \end{equation}$$
    实际使用中，常将指数分布作为各种寿命分布的近似，如动物的寿命，电子电气元件的寿命，随机服务系统中的服务时间等.
    指数分布具有无记忆性.
    指数分布的期望与方差分别为：$\frac{1}{\lambda}, \frac{1}{\lambda^2}$.
• Normal Distribution/Gaussian Distribution(正态分布/高斯分布)
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, x \in (-\infty,+\infty)$$
  其中$\mu, \sigma$均为常数，分别为其的期望与方差，且$\sigma>0$，则称随机变量$X$服从参数为$\mu, \sigma$的正态分布，也称随机变量$X$为正态变量，记作$X \sim N(\mu, \sigma^2)$.
    正态分布的分布函数为：
  $$F(x)=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt, x \in (-\infty,+\infty)$$
    特别地，当$\mu=0, \sigma=1$时的正态分布叫做标准正态分布，记作$X \sim N(0,1)$，它的概率密度使用$\phi(x)$表示，为：
  $$\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}, x \in (-\infty,+\infty)$$
  其分布函数使用$\Phi(x)$表示，为：
  $$\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}dt, x \in (-\infty,+\infty)$$
  这样就有：
  $$\Phi(-x)=1-\Phi(x)$$
  并且，正态分布$N(\mu,\sigma^2)$的分布函数与标准正态分布$N(0,1)$的分布函数$\Phi(x)$有：
  $$F(x)=\Phi(\frac{x-\mu}{\sigma})$$
    正态分布的期望与方差分别为：$\mu, \sigma^2$.
• Lognormal Distribution(对数正态分布)
  定义：若随机变量$X$的对数服从正态分布，那么该随机变量服从对数正态分布，其概率密度为
  $$f(x)=\frac{1}{\sigma x \sqrt{2 \pi}}e^{-\frac{(ln x-\mu)^2}{2 \sigma^2}}, x>0$$
  其中$\mu, \sigma$均为常数，且$\sigma>0$，则称随机变量$X$服从参数为$\mu, \sigma$的对数正态分布，也称随机变量$X$为对数正态变量，记作$X \sim LN(\mu, \sigma^2)$，注意：$\mu,\sigma$不是它的期望与方差.
    对数正态分布的分布函数为：
  $$F(x)=\int_{0^+}^{x}f(t)dt=\Phi(\frac{ln x-\mu}{\sigma})$$
    对数正态分布的期望与方差分别为：$e^{\mu+\frac{\sigma^2}{2}}, e^{2\mu+\sigma^2}e^{\sigma^2-1}$.

• Gamma Distribution(伽马分布)
  先导知识：

  • 阶乘：n!=n(n-1)(n-2)…1

  • Gamma(伽马)函数：Gamma函数是阶乘的在实数域与复数域上的拓展，记为$\Gamma(x)$.

    • 在实数域上伽马函数定义为：
      $$\Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt$$
    • 在复数域（其中Re(z)>0，即实数部分大于0）上伽马函数定义为：
      $$\Gamma(z)=\int_0^{+\infty}t^{z-1}e^{-t}dt$$

    通过分部积分，可以得到：
    

    $$\Gamma(x+1)=x\Gamma(x)$$
    对于正整数$n$，有：
    $$\Gamma(n)=\int_0^{+\infty}t^{n}e^{-t}dt=(n-1)!$$
    那么问题来了：
    • 这个如此奇怪的函数是如何发现的呢?
        这就与一些数学大豪有关了，比如哥德巴赫、贝努利、欧拉、高斯等，详细参见神奇的gamma函数.
    • 为何$\Gamma(n) \neq n!$而是$\Gamma(n) \neq (n-1)!$?
        欧拉早期的Gamma函数便是定义为$\Gamma(n) \neq n!$，后来对其进行了修正为$\Gamma(n) \neq (n-1)!$(具体原因不得而知)，可能欧拉研究了
      $$B(m,n)=\int_{0}^{1}x^{m-1}(1-x)^{n-1}dx$$
      这个函数便是Beta函数，如果$\Gamma(n) \neq (n-1)!$，那么有
      $$B(m,n)=\frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)}$$
      该函数是具有非常漂亮的对称形式. 如果$\Gamma(n) \neq n!$，那么令
      $$E(m,n)=\int_{0}^{1}x^m(1-x)^ndx$$
      则有
      $$E(m,n)=\frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n+1)}$$
      这个形式显然不如$B(m,n)$那么优美，而数学家总是很在乎数学公式的美感的.
      定义：若随机变量$X$的概率密度为
      $$f(x)=\frac{1}{\beta^\alpha \Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}}, x>0$$
      其中，$\alpha$形状参数(shape parameter)，$\beta$尺度参数(scale parameter)均为常数，则称随机变量$X$服从参数为$\alpha, \beta$的伽马分布，记作$X \sim Ga(\alpha, \beta)$.
        Gamma分布函数为：
      $$F(x)=\int_0^x f(u)du=\frac{\gamma(\alpha,\frac{x}{\beta})} {\Gamma(\alpha)}$$
      其中
      $$\gamma(\alpha,\frac{x}{\beta})=\int_0^{\frac{x}{\beta}}t^{\alpha-1}e^{-t}$$
        若$\alpha$是正整数，上式是一个Erlang分布：
      $$F(x)=1-\sum_{i=0}^{\alpha-1}\frac{(\beta x)^i}{i!}e^{-\beta x}=e^{-\beta x}\sum_{i=\alpha}^{\infty}\frac{(\beta x)^i}{i!}$$
        Gamma分布的期望为$\alpha\beta$，方差为$\alpha\beta^2$. Gamma分布即为：随机变量$X$ 为等到第$\alpha$件事发生所需等待时间.
• Beta Distribution(Beta分布)
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{1}{B(a,b)}x^{a-1}(1-x)^{b-1}, 0<x<1$$
  其中，$a>0, b>0$均为常数，$B(a,b)=\frac{\Gamma{a+b}}{\Gamma(a)\Gamma(b)}$，那么随机变量$X$服从参数为$a, b$的贝塔分布，记为$X \sim B(a,b)$.
    贝塔分布的分布函数为：
  $$F(x)=\int_{0}^{x}f(t)dt$$
    Beta分布的期望与方差分别为：$\frac{\alpha}{\alpha+\beta}, \frac{\alpha\beta}{\alpha+\alpha\beta^2+\beta+1}$.
• Dirichlet Distribution(狄利克雷分布)
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)...\Gamma(\alpha_K)}\prod_{k=1}^{K}\mu_k^{\alpha_k-1}$$
  其中，$\vec{\mu}=(\mu_1,...,\mu_K),\vec{\alpha}=(\alpha_0,...,\alpha_K)$中的每一个分量为均常数，并且$\sum_k\mu_k=1, \alpha_0=\sum_{k=1}^{K}\alpha_k$ ，那么随机变量$X$服从参数为$\vec{\mu}, \vec{\alpha}$的狄利克雷分布，记为$X \sim Dir(\vec{\mu},\vec{\alpha})$.
• Rayleigh Distribution(瑞利分布)
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{x}{\sigma^2}e^{\frac{-x^2}{2\sigma^2} }, x \geq 0$$
  其中，$\sigma>0$为常数，那么随机变量$X$服从参数为$\sigma$的瑞利分布，记为$X \sim R(\sigma)$.
    瑞利分布的分布函数为：
  $$F(x)=\int_{0}^{x}f(t)dt$$
    瑞利分布的期望与方差分别为：$\frac{\pi}{2}\sigma, \frac{4-\pi}{2}\sigma^2$
• Cauchy Distribution(柯西分布)
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{1}{\pi\gamma[1+\frac{(x-x_0)^2}{\gamma}]}, x \in (-\infty,+\infty)$$
  其中，$x_0位置参数, \gamma(\gamma>0)$尺度参数均为常数，那么随机变量$X$服从参数为$x_0, \gamma$的柯西分布，记为$X \sim C(x_0, \gamma)$.
    柯西分布的分布函数为：
  $$F(x)=\int_{-\infty}^{x}f(t)dt=\frac{\pi}arctan(\frac{x-x_0}{\gamma})+\frac{1}{2}, x \in (-\infty,+\infty)$$
    柯西分布的期望与方差均不存在.
• Weibull Distribution(韦伯分布)
    韦伯分布的期望与方差分别为：
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{\beta}{\eta}(\frac{x}{\eta})^{\beta-1}e^{-(\frac{x}{\eta})^{\beta}}, x \geq 0$$
  其中，$\eta>0, \beta>0$均为常数，那么随机变量$X$服从参数为$\eta, \beta$的韦伯分布，记为$X \sim W(\eta, \beta)$.
    韦伯分布的分布函数为：
  $$F(x)=\int_{-0}^{x}f(t)dt=1-e^{-(\frac{x}{\eta})^\beta}$$
    韦伯分布的期望与方差分别为：$\eta\Sigma(\frac{1}{\beta}+1), \eta^2(\Gamma(\frac{2}{\beta}+1)-\Gamma(\frac{1}{\beta}+1))$.
    它的累积分布函数是扩展的指数分布函数，而且，Weibull distribution与很多分布都有关系。如，当$\beta=1$，它是指数分布；$\beta=2$时，是Rayleigh Distribution(瑞利分布).
• Laplacian Distribution(拉普拉斯分布)
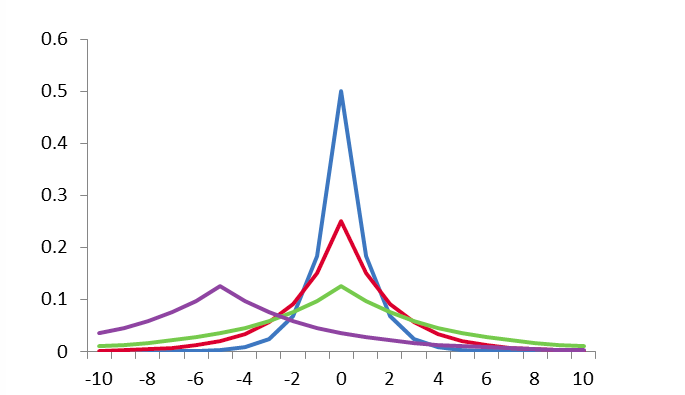
  定义：若随机变量$X$的概率密度为
  $$f(x)=\frac{1}{2b}e^{-\frac{|x-\mu|}{b}}$$
  其中，$\mu位置参数, b(b>0)尺度参数$均为常数，那么随机变量$X$服从参数为$\mu, b$的拉普拉斯分布，记为$X \sim L(\mu, b)$.
    概率密度函数如下图所示：
  
    拉普拉斯分布的分布函数为：
  $$F(x)=\int_{-\infty}^{x}f(t)dt＝\frac{1}{2}[1+sgn(x-u)e^{-\frac{|x-\mu|}{b}}]$$
    拉普拉斯分布的期望与方差分别为：$\mu, 2b^2$.