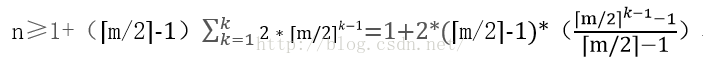数据结构--B 树、B+ 树、B* 树

1.  B 树、B+ 树、B* 树

1.1. 前言

前面讨论的二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced BinarySearch Tree），红黑树(Red-BlackTree )都是内查询算法，被查询的数据都在内存。当查询的数据放在外存，用平衡二叉树作磁盘文件的索引组织时，若以结点为内外存交换的单位，则找到需要的关键字之前，平均要进行lgⁿ次磁盘读操作，而磁盘、光盘的读写时间要比随机存取的内存代价大得多。其二，外存的存取是以“页”为单位的，一页的大小通常是4K字节或2048字节。

因此咱们有面对这样一个实际问题：就是大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的（如果元素数量非常多的话，查找就退化成节点内部的线性查找了），这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下（为什么会出现这种情况，待会在背景知识介绍中有所解释），那么如何减少树的深度（当然是不能减少查询的数据量），一个基本的想法就是：采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）。

也就是说，因为磁盘的操作费时费资源，如果过于频繁的多次查找势必效率低下。那么如何提高效率，即如何避免磁盘过于频繁的多次查找呢？根据磁盘查找存取的次数往往由树的高度所决定，所以，只要我们通过某种较好的树结构减少树的结构尽量减少树的高度，那么是不是便能有效减少磁盘查找存取的次数呢？那这种有效的树结构是一种怎样的树呢？

针对上述特点，1972年R.Bayer和E.M.Cright提出了一种B-树的多路平衡查找树，以适合磁盘等直接存取设备上组织动态查找表（wikipedia中：http://en.wikipedia.org/wiki/B-tree，阐述了B-tree名字来源以及相关的开源地址）。B-树上算法的执行时间主要由读、写磁盘的次数来决定，故一次I/O操作应读写尽可能多的信息。因此B-树的结点规模一般以一个磁盘页为单位。一个结点包含的关键字及其孩子个数取决于磁盘页的大小。

这篇文章所要阐述的第一个主题B-tree，即B树结构(后面，我们将看到，B树的各种操作能使B树保持较低的高度，从而达到有效避免磁盘过于频繁的查找存取操作，从而有效提高查找效率)。

在开始介绍B-tree之前，先了解下相关的硬件知识，才能很好的了解为什么需要B-tree这种外存数据结构。 

1.2. 背景知识介绍

B树和B+广泛应用于文件存储系统以及数据库系统中，在讲解应用之前，我们看一下常见的存储结构：

我们计算机的主存基本都是随机访问存储器(Random-Access Memory，RAM)，他分为两类：静态随机访问存储器（SRAM）和动态随机访问存储器（DRAM）。SRAM比DRAM快，但是也贵的多，一般作为CPU的高速缓存，DRAM通常作为内存。这类存储器他们的结构和存储原理比较复杂，基本是使用电信号来保存信息的，不存在机器操作，所以访问速度非常快，具体的访问原理可以查看CSAPP，另外，他们是易失的，即如果断电，保存DRAM和SRAM保存的信息就会丢失。

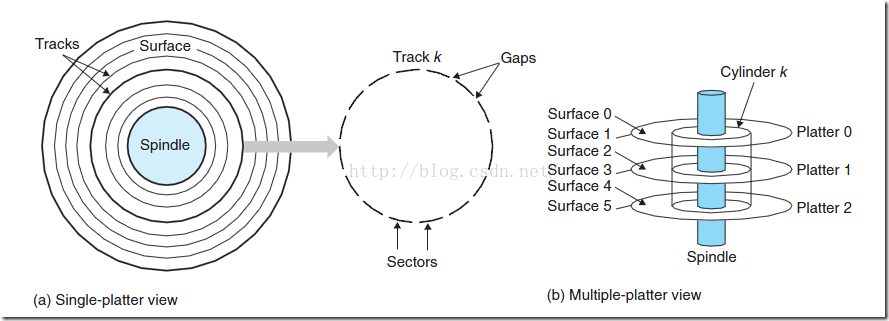
我们使用的更多的是使用磁盘，磁盘能够保存大量的数据，从GB一直到TB级，但是 他的读取速度比较慢，因为涉及到机器操作，读取速度为毫秒级，从DRAM读速度比从磁盘度快10万倍，从SRAM读速度比从磁盘读快100万倍。下面来看下磁盘的结构：

如上图，磁盘由盘片构成,每个盘片有两面，又称为盘面(Surface)，这些盘面覆盖有磁性材料。盘片中央有一个可以旋转的主轴(spindle)，他使得盘片以固定的旋转速率旋转，通常是5400转每分钟(Revolution Per Minute,RPM)或者是7200RPM。磁盘包含一个多多个这样的盘片并封装在一个密封的容器内。上图左，展示了一个典型的磁盘表面结构。每个表面是由一组成为磁道(track)的同心圆组成的，每个磁道被划分为了一组扇区(sector).每个扇区包含相等数量的数据位，通常是（512）子节。扇区之间由一些间隔(gap)隔开,不存储数据。

以上是磁盘的物理结构，现在来看下磁盘的读写操作：

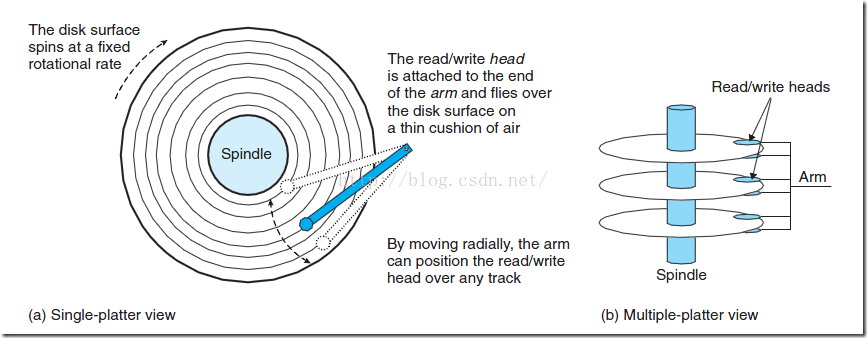
如上图，磁盘用读/写头来读写存储在磁性表面的位，而读写头连接到一个传动臂的一端。通过沿着半径轴前后移动传动臂，驱动器可以将读写头定位到任何磁道上，这称之为寻道操作。一旦定位到磁道后，盘片转动，磁道上的每个位经过磁头时，读写磁头就可以感知到位的值，也可以修改值。对磁盘的访问时间分为 寻道时间，旋转时间，以及传送时间。

由于存储介质的特性，磁盘本身存取就比主存慢很多，再加上机械运动耗费，因此为了提高效率，要尽量减少磁盘I/O，减少读写操作。为了达到这个目的，磁盘往往不是严格按需读取，而是每次都会预读，即使只需要一个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理：

当一个数据被用到时，其附近的数据也通常会马上被使用。

程序运行期间所需要的数据通常比较集中。                                       

由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），因此对于具有局部性的程序来说，预读可以提高I/O效率。

预读的长度一般为页（page）的整倍数。页是计算机管理存储器的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块，每个存储块称为一页（在许多操作系统中，页得大小通常为4k），主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时，会触发一个缺页异常，此时系统会向磁盘发出读盘信号，磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中，然后异常返回，程序继续运行。

文件系统及数据库系统的设计者利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的，在实际实现B-Tree还需要使用如下技巧：

每次新建一个节点的同时，直接申请一个页的空间( 512或者1024)，这样就保证一个节点物理上也存储在一个页里，加之计算机存储分配都是按页对齐的，就实现了一个node只需一次I/O。如，将B树的度M设置为1024，这样在前面的例子中，600亿个元素中只需要小于4次查找即可定位到某一存储位置。

同时在B+树中，内节点只存储导航用到的key，并不存储具体值，这样内节点个数较少，能够全部读取到主存中，外接点存储key及值，并且顺序排列，具有良好的空间局部性。所以B及B+树比较适合与文件系统的数据结构。另外B/B+树也经常用做数据库的索引，这方面推荐您直接看张洋的MySQL索引背后的数据结构及算法原理 这篇文章，这篇文章对MySQL中的如何使用B+树进行索引有比较详细的介绍，推荐阅读。

1.3. B-树 

1.3.1.  什么是B-树

具体讲解之前，有一点，再次强调下：B-树，即为B树。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是一种树。而事实上是，B-tree就是指的B树。

从上面背景知识介绍中我们知道，B-tree 与一般的平衡树如 AVL-Tree，Red-Black Tree 的一个显著区别是 B-tree 的每个内结点可以拥有很多个 Children（这个度量被称为「内结点出度」，下文会更深入的讨论之），那么我们可以在技术上使 B-tree 的结点大小为磁盘一个页的大小，并且在新建结点时直接申请一个页大小的空间，使得结点的物理存储位置也是在一个页里，这样就能实现存取一个结点只需一次磁盘 I/O。在最坏情况下，B-tree 的一次检索最多需要 （树的高度）次的磁盘 I/O。记 为B-tree 中的 Key 的数据量， 为内结点出度的二分之一，则我们可以证明 ，渐进复杂度为 。这意味着，一棵拥有 200 万 Key 的 B-tree，在内结点出度为 200 时它的树高 最多为 3。实际上，为了取得更大的内结点出度，各个数据库一般会采用 B-tree的变种如 B+-tree，B*-tree来实现索引，比如 MySQL 的存储引擎 InnoDB 就采用 B+-tree 来实现聚簇索引。

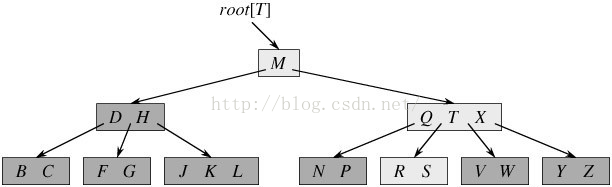
如下图所示，即是一棵B树，一棵关键字为英语中辅音字母的B树，现在要从树中查找字母R（包含n[x]个关键字的内结点x，x有n[x]+1]个子女（也就 是说，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女）。所有的叶结点都处于相同的深度，下图中浅色的结点为查找字母R时要检查的结点）：

 

相信，从上图你能轻易的看到，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女。如含有2个关键字D H的内结点有3个子女，而含有3个关键字Q T X的内结点有4个子女。

B树的定义，从下文中，你将看到，或者是用阶，或者是用度，如下段文字所述：

Unfortunately,the literature on B-trees is not uniform in its use of terms relating toB-Trees. (Folk & Zoellick 1992, p. 362) Bayer & McCreight (1972),Comer (1979), and others define the order of B-tree as the minimum number ofkeys in a non-root node. Folk & Zoellick (1992) points out that terminologyis ambiguous because the maximum number of keys is not clear. An order 3 B-treemight hold a maximum of 6 keys or a maximum of 7 keys. (Knuth 1998,TAOCP p.483) avoids the problem by defining the order to be maximum number of children(which is one more than the maximum number of keys).

   from: http://en.wikipedia.org/wiki/Btree#Technical_description。

清华大学出版社的《数据结构（C语言版）》（2007年版），编著者为严蔚敏，吴伟民。该教材中关于 B-tree 的定义摘录如下：

一棵m 阶的 B-树，或为空树，或为满足下列特性的 m叉树：

1)  树中每一个结点至多有m 棵子树；

2)  若根结点不是叶子结点，则至少有两棵子树；

3)  除根结点之外的所有非终端结点至少有m/2 棵子树；

4)  所有的非终端结点中包含下列信息数据 (n,A₀,K₁,A₁,K₂,A₂,…,K_n,A_n)， 其中：K_i(i=1,…,n) 为关键字，且K_i<K_i+1(i=1,…,n-1)；A_i(i=0,…,n)为指向子树根结点的指针，且指针A_i-1 所指子树中所有结点的关键字均小于K_i(i=1,…,n)，A_n 所指子树中所有结点的关键字均大于K_n ，n(⌈m/2-1⌉ ≤n≤m-1)为关键字的个数（或n+1 为子树个数）；

5)  所有的叶子结点都出现在同一层次上，并且不带信息（可以看作是外部结点或查找失败的结点，实际上这些结点不存在，指向这些结点的指针为空）。

比如，一棵3阶B-树，m=3。它满足： 

（1）每个结点的孩子个数小于等于3。 

（2）除根结点外，其他结点至少有=2个孩子。 

（3）根结点有两个孩子结点。 

（4）除根结点外的所有结点的n大于等于=1，小于等于2。 

（5）所有叶结点都在同一层上。

下面看Introduction to Algorithms（《算法导论》）一书中关于 B-tree 的定义。摘录原书第三版中 B-tree 定义的原文如下：

A B-tree T is a rooted tree (whose root is T.root ) having the following properties:

• Every node has the following attributes:

• x.n , the number of keys currently stored innode x,
• the keys x.n themselves, x.key₁ ,x.key₂,…,x.key_x.n , stored in non-decreasing order, so that x.key₁≤x.key₂ ≤… ≤x.key_x.n,
• x.leaf, a Boolean value that is TRUE if x is a leaf and FALSE if x is an internal node.

• Each internal node x also contains x.n+1  pointers x.c₁,x.c₂,…,x.c_x.n+1 to its children. Leaf nodes have nochildren, and so their c_i attributes are undefined.
• The keys x.key_i separate the ranges of keys stored ineach sub-tree: if key_i is any key stored in the sub-tree with root x.c_i, then k₁≤x.key₁ ≤x.key₂ ≤… ≤x.key_x.n ≤x.key_{x.n +1} .
• All leaves have the same depth, which is the tree’s height h .
• l  Nodes have lower and upper bounds on the number of keys they cancontain. We express these bounds in terms of a fixed integer t≥2  called the minimum degreeof the B-tree:

• Every node other than the root must have at least  t-1 keys. Every internal node other than theroot thus has at leastchildren. If the tree is non-empty, theroot must have at least one key.
• Every node may contain at most  2t-1 keys. Therefore, an internal node may have at most 2t children. We say that a node is full ifit contains exactly 2t-1 keys.

 

再看高德纳的经典著作 The Art of Computer Programming （《计算机程序设计艺术》）关于 B-tree 的定义，原书第二版原文摘录如下：

A B-treeof order m is a tree that satisfies the following properties:

1)     Every node has at most m children.

2)     Every node, except for theroot and the leaves, has at least m/2 children.

3)     The root has at least 2 children (unless it is a leaf).

4)     All leaves appear on the samelevel, and carry no information.

5)     A non-leaf node with k children contains k-1 keys.

(As usual, a leaf is a terminal node, one with nochildren. Since the leaves carry no information, we may regard them as externalnodes that aren't really in the tree, so that A is a pointer to a leaf.)

要补充说明的是，上述 B-tree 定义中第二条 m/2为向上取整，亦即⌈m/2⌉，这一点在原书下文中亦有说明。

最后摘录的是论文 Organization and Maintenance of Large Ordered Indexes （下面简称「论文」）中的定义：

Def. 2.1. Let h≥0 be an integer, k a natural number. A directed tree T is in the class  t(k,h) of B-tree if T is either empty (h=0) or has the following properties:

1)      Each path from the root to any leaf has the same length h, also called the hight of T , i.e.,  h=number of nodes in path .

2)      Each node except the root and the leaves has at least k+1 sons. The root is a leaf or has at least two sons.

3)      Each node has at most 2k+1 sons.

感兴趣的话，不妨参看 Wikipedia 上 B-tree 的词条（http://en.wikipedia.org/wiki/B-tree），与以上摘录做一个对比。下面分析上述定义之间的差异。

不难看出，《数据结构（C语言版）》的定义参考了《计算机程序设计艺术》的定义，所以它们可以归为同一个定义。

可以看到:

• 差异之一是，关于leaf 的定义并不统一。《计算机程序设计艺术》一书中主张 leaf 是包含数据的最底层结点的下一层，而《算法导论》一书与「论文」则主张最底层包含数据的结点即为 leaf。实际上，关于 leaf 定义的二义性不难理解。因为 B-tree 的实现有很多种，有些实现中，叶子结点本身可能包含了关键字与数据的全部信息，另外一些实现中叶子结点也许仅仅包含了指向这些数据的指针。只要能恰当表示「B-tree的最底层」这个概念，所有这些定义都是可行的。所以说 leaf 如何定义并不关系到 B-tree 的核心概念。
• 差异之二，亦是问题中提到的疑问，关于 B-tree 的 Order，或翻译为「度」的定义并不统一。《算法导论》一书中定义了一个称为「最小度数t 」的概念，表示非根的内结点至少拥有的子女数量，并且规定内结点最多拥有的子女数为 2t。《计算机程序设计艺术》一书中定义的「度 m」表示一个结点所能拥有的最大子女数，并且非根内结点至少拥有⌈m/2⌉ 个子女。这样，非根内结点的最小子女数并不固定，而是和「度 m」的奇偶性有关。而「论文」中并没有明确给出度的概念，而是给出了一个自然数 k，表示非根内结点至少拥有的关键字（key）的数量，并且最多能拥有的 key 数量为 2k，亦即最大子女数是 2k+1。

我曾经尝试统一上述不同定义中关于「度」的概念，比如试图将《算法导论》中的 经过一些数学上的推演后得到《计算机程序设计艺术》中的 。这样的尝试得到的结果令人费解。因为按照《算法导论》的定义推演，最简的 B-tree 是一棵 2-3-4 tree（每个非根内结点可以有 2 个，3 个，4 个子女）。而按照《计算机程序设计》的定义推演，最简的 B-tree 是一棵 2-3 tree（每个非根内结点可以拥有 2 个或 3 个子女）。

理解上述「费解」差异的突破口是理解设计 B-tree 的「目的」与 B-tree 的「性质」。

回顾之前总结关于 B-tree 的三个要点可以看到，设计 B-tree 的「目的」是为了减少磁盘 I/O 的次数。所有定义与实现都要为达到这个目的而考虑。B-tree 的「性质」是：作为一个数据结构，它是一棵平衡的多路查找树，所有叶子结点都在同一层次，拥有相同的深度。为维护这个性质，B-tree 在进行插入与删除操作时需要在适当的时机分裂与合并结点。为使插入与删除操作能顺利进行，B-tree 要求内结点满足至少「半满」，至多「全满」的性质，这样：

1)  当一个新 key 插入一个原本「全满」的结点使得结点需要分裂时，我们总能找到合理的分裂点，且分裂后产生的新结点满足「半满」。

2)  进行删除操作时，能够保证让删除后不满足「半满」性质的结点通过合并而满足「半满」。

3)  同时仍能维护整棵树「平衡」的性质。

「度」的概念就是为了定量描述「半满」、「全满」这两个性质而引进的度量（需要注意的是，「半满」与「全满」并不是维护 B-tree 平衡的必要条件。例如， B*-tree 要求非根内结点至少「三分之二满」，至多「全满」。这也意味着其插入与删除操作相较于 B-tree 会略有差异）。

这样，可以解释关于「度」的定义的差异了。

前文引用各文献时并没有依从时间顺序。历史上，先有「论文」，再有《计算机程序设计艺术》，再有《算法导论》。对于宣告 B-tree 正式诞生的「论文」，根据 Wikipedia 上 B-tree 词条的描述，当时同样存在其他 B-tree 的定义规定最少的非根内结点 key 的数量为 k，而这些定义对最大 key 数量的规定并不统一，这意味着最大key 的数量不确定，可能为 2k，也可能为2k+1 。

高德纳在他的《计算机科学与艺术》一书中通过定义非根内结点的最大子女数 来避免了这个问题。但是根据《计算机科学与艺术》对 B-tree 的「原始定义」（高德纳在后文中对「原始定义」做了优化），这样的 B-tree（或者说经典的 B-tree）在进行插入删除操作时，如果遇到一个结点需要分裂或者两个结点需要合并，那么在 DFS 过程中需要回溯到父结点，这意味着一次多余的磁盘 I/O。是否有办法去掉这一多余的磁盘I/O？Wikipedia 中提到：

An improved algorithm supports a single pass down the tree fromthe root to the node where the insertion will take place, splitting any fullnodes encountered on the way. This prevents the need to recall the parent nodesinto memory, which may be expensive if the nodes are on secondary storage.However, to use this improved algorithm, we must be able to send one element tothe parent and split the remaining U-2elements into two legal nodes, without adding a new element.This requires U = 2L rather than U = 2L-1, which accounts for why some textbooks impose this requirementin defining B-trees.

大意为：可以找到一种改进算法，让插入操作的一趟 DFS过程中，遇到全满结点就进行分裂操作，而非等到加入一个新 key导致溢出时才进行分裂操作。此时不需要重新读取父结点到主存。然而该改进要求「全满」与「半满」的数量关系严格满足倍数关系 U = 2L（这里即高德纳的 m）。因为我们需要保证在分裂「全满」结点时，提取一个 key并将其上升到父结点后，剩下的结点仍然能分裂为两个合法的新结点。

可以看到《算法导论》中关于 B-tree 的定义正好满足了这个要求。《算法导论》定义的 t 是「半满」情况下一个非根内结点的子女数，则该「半满」结点拥有 t-1 个 key。因此「全满」结点拥有 2t 个子女（即 2t-1个 key）。若「全满」结点发生分裂，则在提取一个 key 后剩下 2t - 2 个 key，正好可以分裂为两个拥有 t-1 个 key 的「半满」结点。这样，我们可以认为《算法导论》实际上是对经典的 B-tree 做了一个改进，由此导致了定义上的差异。

我的理解是，B-tree 的多种定义只是形式上的约束，最终目的是为了描述这个「平衡的多路查找树」的本质。

1.3.2.  B-树的算法思想

1、B-树的查找

B-树的查找过程：根据给定值查找结点和在结点的关键字中进行查找交叉进行。首先从根结点开始重复如下过程：

  若比结点的第一个关键字小，则查找在该结点第一个指针指向的结点进行；若等于结点中某个关键字，则查找成功；若在两个关键字之间，则查找在它们之间的指针指向的结点进行；若比该结点所有关键字大，则查找在该结点最后一个指针指向的结点进行；若查找已经到达某个叶结点，则说明给定值对应的数据记录不存在，查找失败。

2、B-树的插入

插入的过程分两步完成：

1)  利用前述的B-树的查找算法查找关键字的插入位置。若找到，则说明该关键字已经存在，直接返回。否则查找操作必失败于某个最低层的非终端结点上。

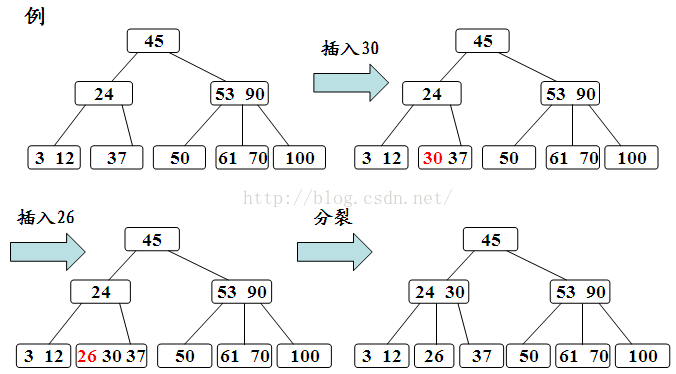
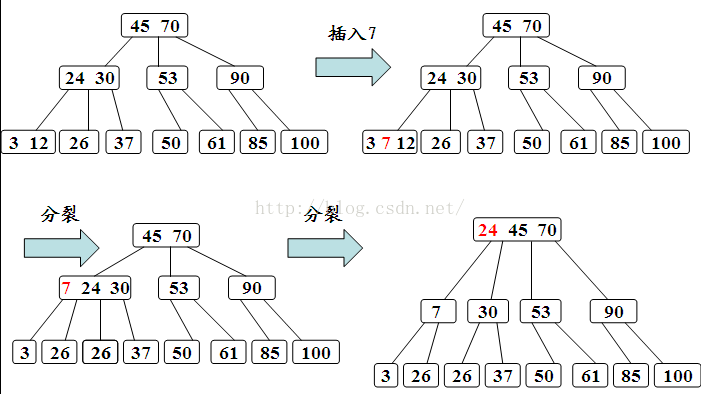
2)  判断该结点是否还有空位置。即判断该结点的关键字总数是否满足n<=m-1。若满足，则说明该结点还有空位置，直接把关键字k插入到该结点的合适位置上。若不满足，说明该结点己没有空位置，需要把结点分裂成两个。

分裂的方法是：生成一新结点。把原结点上的关键字和k按升序排序后，从中间位置把关键字（不包括中间位置的关键字）分成两部分。左部分所含关键字放在旧结点中，右部分所含关键字放在新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过（m-1），则要再分裂，再往上插。直至这个过程传到根结点为止。

3、B-树的删除

在B-树上删除关键字k的过程分两步完成：

1)  利用前述的B-树的查找算法找出该关键字所在的结点。然后根据k所在结点是否为叶子结点有不同的处理方法。

2)  若该结点为非叶结点，且被删关键字为该结点中第i个关键字key[i]，则可从指针son[i]所指的子树中找出最小关键字Y，代替key[i]的位置，然后在叶结点中删去Y。

因此，把在非叶结点删除关键字k的问题就变成了删除叶子结点中的关键字的问题了。

在B-树叶结点上删除一个关键字的方法是：首先将要删除的关键字k直接从该叶子结点中删除。然后根据不同情况分别作相应的处理，共有三种可能情况：

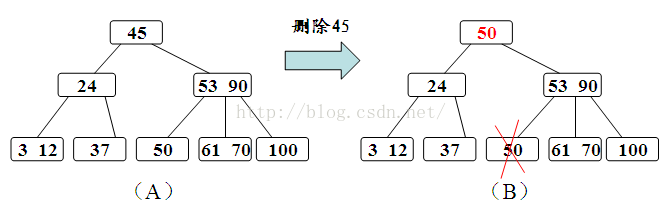
1)  如果被删关键字所在结点的原关键字个数n>=ceil(m/2)，说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单，只需从该结点中直接删去关键字即可。

2)  如果被删关键字所在结点的关键字个数n等于ceil(m/2)-1，说明删去该关键字后该结点将不满足B-树的定义，需要调整。

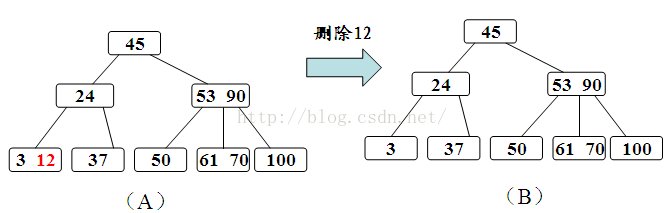
调整过程为：如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右（左）兄弟结点中的关键字数目大于ceil(m/2)-1。则可将右（左）兄弟结点中最小（大）关键字上移至双亲结点。而将双亲结点中小（大）于该上移关键字的关键字下移至被删关键字所在结点中。

3)  如果左右兄弟结点中没有“多余”的关键字，即与该结点相邻的右（左）兄弟结点中的关键字数目均等于ceil(m/2)-1。这种情况比较复杂。需把要删除关键字的结点与其左（或右）兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后，该结点中剩余的关键字加指针，加上双亲结点中的关键字K_i一起，合并到A_i（是双亲结点指向该删除关键字结点的左（右）兄弟结点的指针）所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于ceil(m/2)-1，则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。

总之，设所删关键字为非终端结点中的K_i，则可以指针A_i所指子树中的最小关键字Y代替Ki，然后在相应结点中删除Y。对任意关键字的删除都可以转化为对最下层关键字的删除。

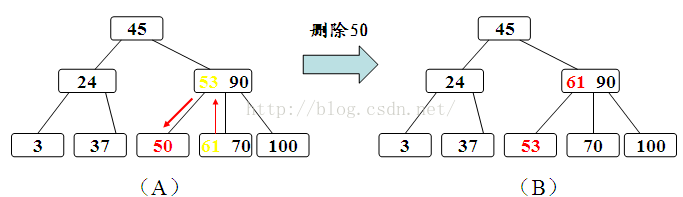
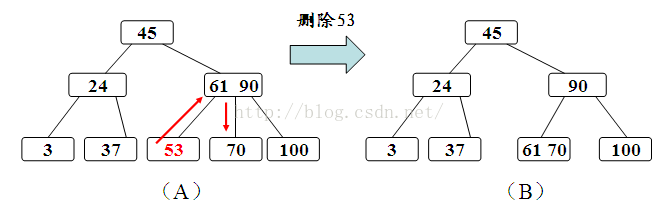
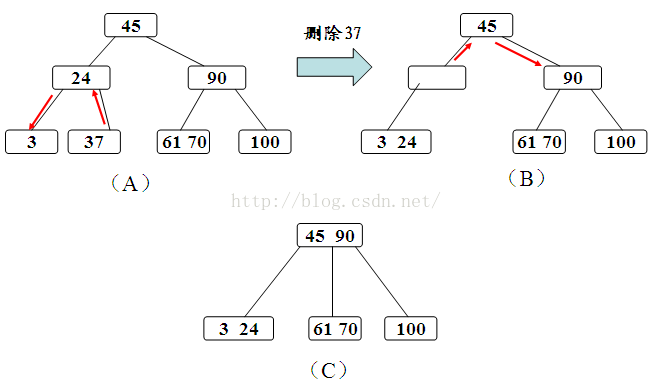
如图示：

a、被删关键字K_i所在结点的关键字数目不小于ceil(m/2)，则只需从结点中删除K_i和相应指针A_i，树的其它部分不变。

b、被删关键字K_i所在结点的关键字数目等于ceil(m/2)-1，则需调整。调整过程如上面所述。

c、被删关键字K_i所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1，假设该结点有右兄弟，且其右兄弟结点地址由其双亲结点指针A_i所指。则在删除关键字之后，它所在结点的剩余关键字和指针，加上双亲结点中的关键字K_i一起，合并到A_i所指兄弟结点中（若无右兄弟，则合并到左兄弟结点中）。如果因此使双亲结点中的关键字数目少于ceil(m/2)-1，则依次类推。

1.3.3.   复杂度分析

B-树查找包含两种基本动作：

●在B-树上查找结点

●在结点中找关键字

由于B-树通常存储在磁盘上，则前一查找操作是在磁盘上进行的，而后一查找操作是在内存中进行的，即在磁盘上找到指针p 所指结点后，先将结点中的信息读入内存，然后再利用顺序查找或折半查找查询等于K 的关键字。显然，在磁盘上进行一次查找比在内存中进行一次查找的时间消耗多得多。

因此，在磁盘上进行查找的次数、即待查找关键字所在结点在B-树上的层次树，是决定B树查找效率的首要因素。

定理：若n≥1，m≥3，则对任意一棵具有n个关键字的m阶B-树，其树高度h至多为log_t^(n+1)/2+1，t= ceil(m/2)。也就是说根结点到关键字所在结点的路径上涉及的结点数不超过log_t^(n+1)/2+1。推理如下：

可按二叉平衡树进行类似分析。首先，讨论m阶B树各层上的最少结点数。

1)  第一层为根，至少一个结点，根至少有两个孩子，因此在第二层至少有两个结点。

2)  除根和树叶外，其它结点至少有⌈m/2⌉个孩子,因此第三层至少有2*⌈m/2⌉个结点,在第四层至少有2*⌈m/2⌉²个结点…

3)  那么在第k+1层至少有2*⌈m/2⌉^k-1个结点（因为计算B树高度时，叶结点所在层不计算在内）,每个节点含有的关键字为⌈m/2⌉-1，而必然有：

n≥2*⌈m/2⌉^k-1-1

即

k≤log_⌈m/2⌉^(n+1)/2+1

也就是说在n个关键字的B树查找，从根节点到关键字所在的节点所涉及的节点数不超过：

log_⌈m/2⌉^(n+1)/2+1

这个k也就是B树的高度。

1.4.   B+-tree

B+-tree:是应文件系统所需而产生的一种B-tree变形树。

一棵m阶的B+树和m阶的B树的异同点在于：

1.有n棵子树的结点中含有n-1 个关键字； (此处颇有争议，B+树到底是与B树n棵子树有n-1个关键字 保持一致，还是不一致：B树n棵子树的结点中含有n个关键字，待后续查证。暂先提供两个参考链接：①wikipedia http://en.wikipedia.org/wiki/B%2B_tree#Overview；②http://hedengcheng.com/?p=525。

2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B树的叶子节点并没有包括全部需要查找的信息)

3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B树的非终节点也包含需要查找的有效信息)

 

 

a)     为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

1) B⁺-tree的磁盘读写代价更低

B⁺-tree内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

       举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B⁺树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B树就比B⁺树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

2) B⁺-tree的查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
 

1.5.  B*-tree

B*-tree是B⁺-tree的变体，在B⁺树的基础上(所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针)，B*树中非根和非叶子结点再增加指向兄弟的指针；B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。给出了一个简单实例，如下图所示：

 

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

 

1.6.  总结

通过以上介绍，大致将B树，B+树，B*树总结如下：

B树：有序数组+平衡多叉树；

B+树：有序数组链表+平衡多叉树；

B*树：一棵丰满的B+树。

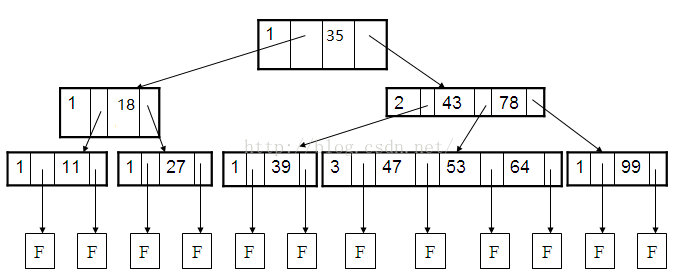
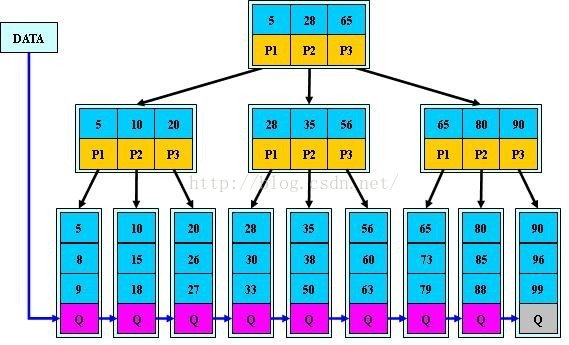
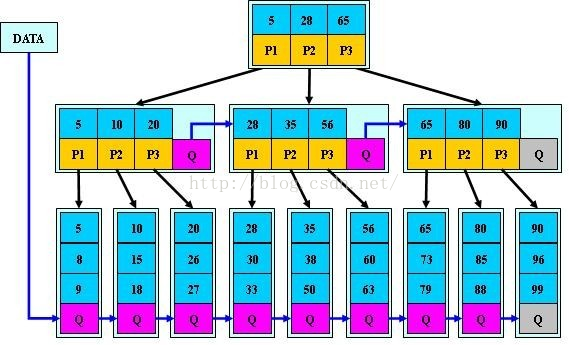
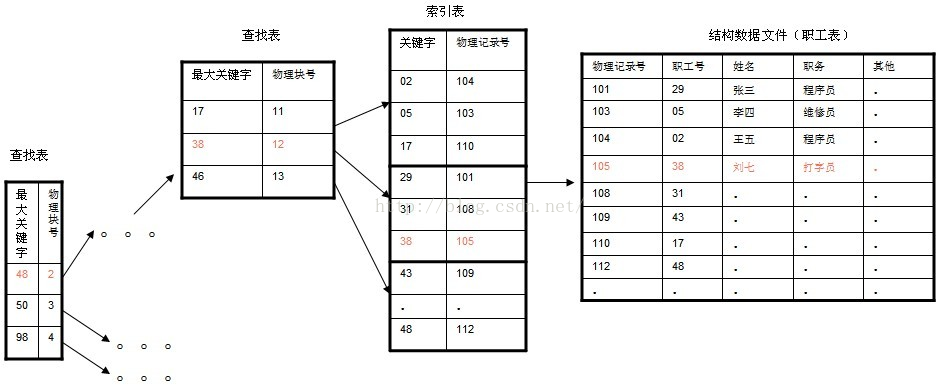
         在大规模数据存储的文件系统中，B~tree系列数据结构，起着很重要的作用，对于存储不同的数据，节点相关的信息也是有所不同，这里根据自己的理解，画的一个查找以职工号为关键字，职工号为38的记录的简单示意图。(这里假设每个物理块容纳3个索引，磁盘的I/O操作的基本单位是块（block),磁盘访问很费时，采用B+树有效的减少了访问磁盘的次数。）

走进搜索引擎的作者梁斌老师针对B树、B+树给出了他的意见（为了真实性，特引用其原话，未作任何改动）： “B+树还有一个最大的好处，方便扫库，B树必须用中序遍历的方法按序扫库，而B+树直接从叶子结点挨个扫一遍就完了，B+树支持range-query非常方便，而B树不支持。这是数据库选用B+树的最主要原因。

    比如要查 5-10之间的，B+树一把到5这个标记，再一把到10，然后串起来就行了，B树就非常麻烦。B树的好处，就是成功查询特别有利，因为树的高度总体要比B+树矮。不成功的情况下，B树也比B+树稍稍占一点点便宜。

    B树比如你的例子中查，17的话，一把就得到结果了，
有很多基于频率的搜索是选用B树，越频繁query的结点越往根上走，前提是需要对query做统计，而且要对key做一些变化。

    另外B树也好B+树也好，根或者上面几层因为被反复query，所以这几块基本都在内存中，不会出现读磁盘IO，一般已启动的时候，就会主动换入内存。”非常感谢。

   mysql 底层存储是用B+树实现的，知道为什么么。内存中B+树是没有优势的，但是一到磁盘，B+树的威力就出来了。

参考文献以及推荐阅读：

1.      http://en.wikipedia.org/wiki/Btree（给出了国外一些开源地址）

2.     http://en.wikipedia.org/wiki/Btree#Technical_description

3.      http://cis.stvincent.edu/html/tutorials/swd/btree/btree.html（include C++ source code）

4.      http://slady.net/java/bt/view.php（如果了解了B-tree结构，该地址可以在线对该结构进行查找（search），插入(insert)，删除(delete)操作。）

5.     Guttman, A.; “R-trees: adynamic index structure for spatial searching,” ACM, 1984, 14

6.     http://www.cnblogs.com/CareySon/archive/2012/04/06/2435349.html；

7.     http://baike.baidu.com/view/298408.htm。

8.     http://www.cnblogs.com/leoo2sk/archive/2011/07/10/mysql-index.html （介绍了mysql中myisam和innodb这两种引擎的内部索引机制，以及对不同字段的索引时，检索效率上的对比，主要也是基于其内部机制的理解）

9.     http://www.oschina.net/news/31988/mysql-indexing-best-practices （MySQL索引最佳实践）；

10.    http://idlebox.net/2007/stx-btree/ （此页面包含 B 树生成构造的一些演示 demo ）。