B树与B+树
B树
B树的定义
一个m阶的B树,就是每一个非叶子节点拥有不超过m个子孩子,也可以定义为非叶子节点最多有m个查找路径(当m=2就是二叉,m=3就是三叉)
真实得到数据集存储在叶子节点和非叶子结点上。B树需要符合下面的一些限制:
1、从根节点到叶子节点的每一条路径都拥有相同的长度
2、如果一个节点拥有n个孩子,那么他就拥有n-1个元素
3、除了根节点和叶子节点,每个非叶子结点(中间的节点)都最少拥有ceil(m/2)上限个子节点
4、关键字数:枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2);(因为关键字数量等于n-1,n>=ceil(m/2))
5、根节点如果不是一个叶子节点,就至少有两个孩子
排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则;
对于m阶的B树:
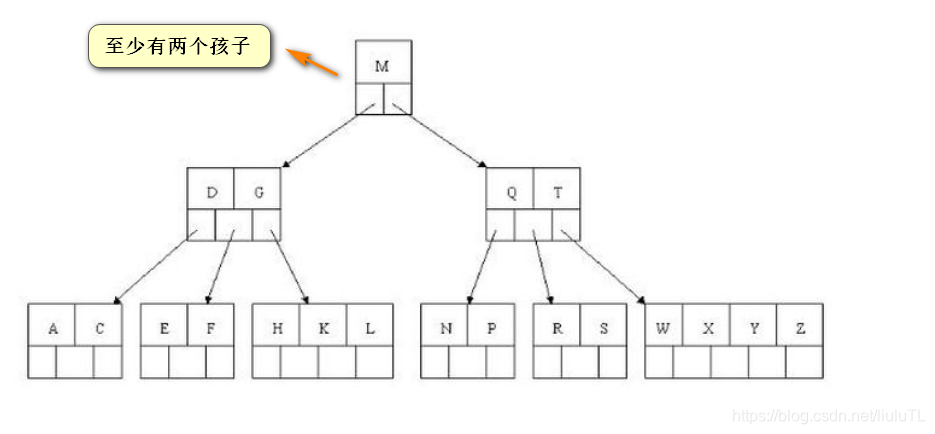
B树的查询
如上图我要从上图中找到E字母,查找流程如下
(1)获取根节点的关键字进行比较,当前根节点关键字为M,E<M(26个字母顺序),所以往找到指向左边的子节点(二分法规则,左小右大,左边放小于当前节点值的子节点、右边放大于当前节点值的子节点);
(2)拿到关键字D和G,D<E<G 所以直接找到D和G中间的节点;
(3)拿到E和F,因为E=E 所以直接返回关键字和指针信息(如果树结构里面没有包含所要查找的节点则返回null);
B树的插入
定义一个5阶树(平衡5路查找树;),现在我们要把3、8、31、11、23、29、50、28 这些数字构建出一个5阶树出来;
遵循规则:
(1)节点拆分规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须<=5-1(这里关键字数>4就要进行节点拆分);
(2)排序规则:满足节点本身比左边节点大,比右边节点小的排序规则;
- 先插入 3、8、31、11
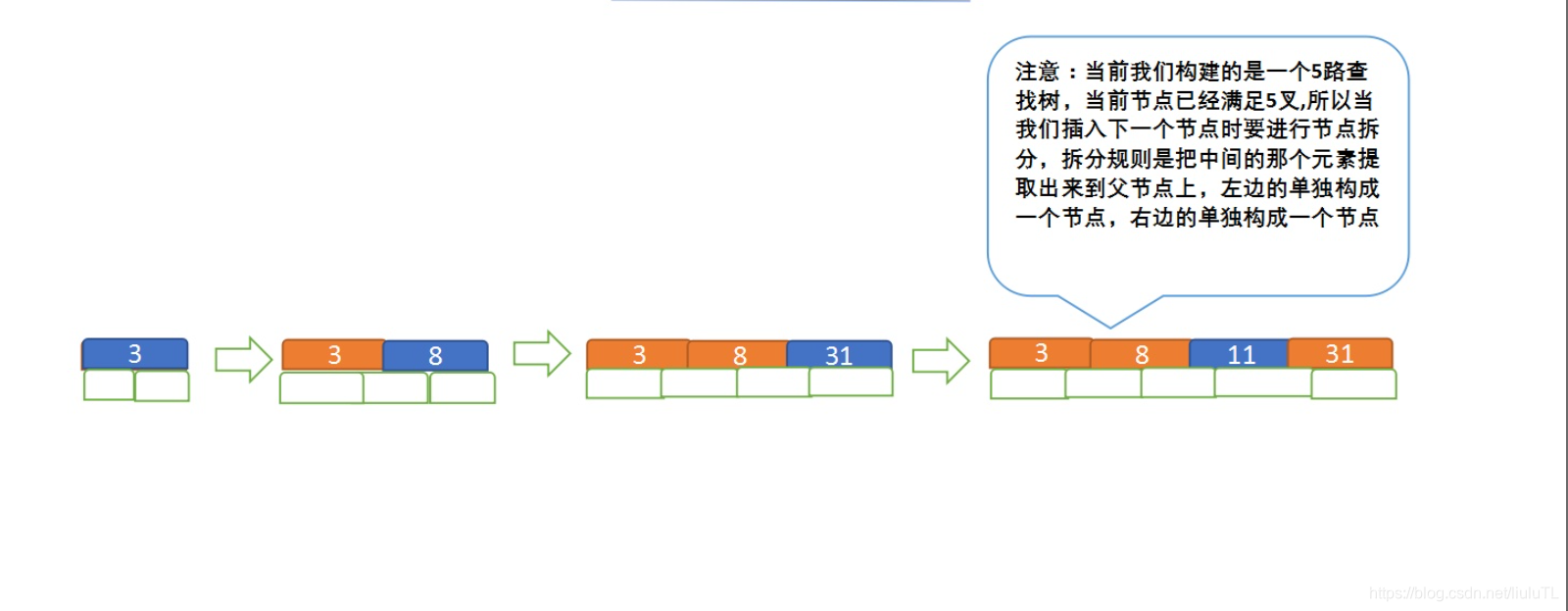
再插入23、29(当等于5时,先排序,将中间的元素进行分裂)
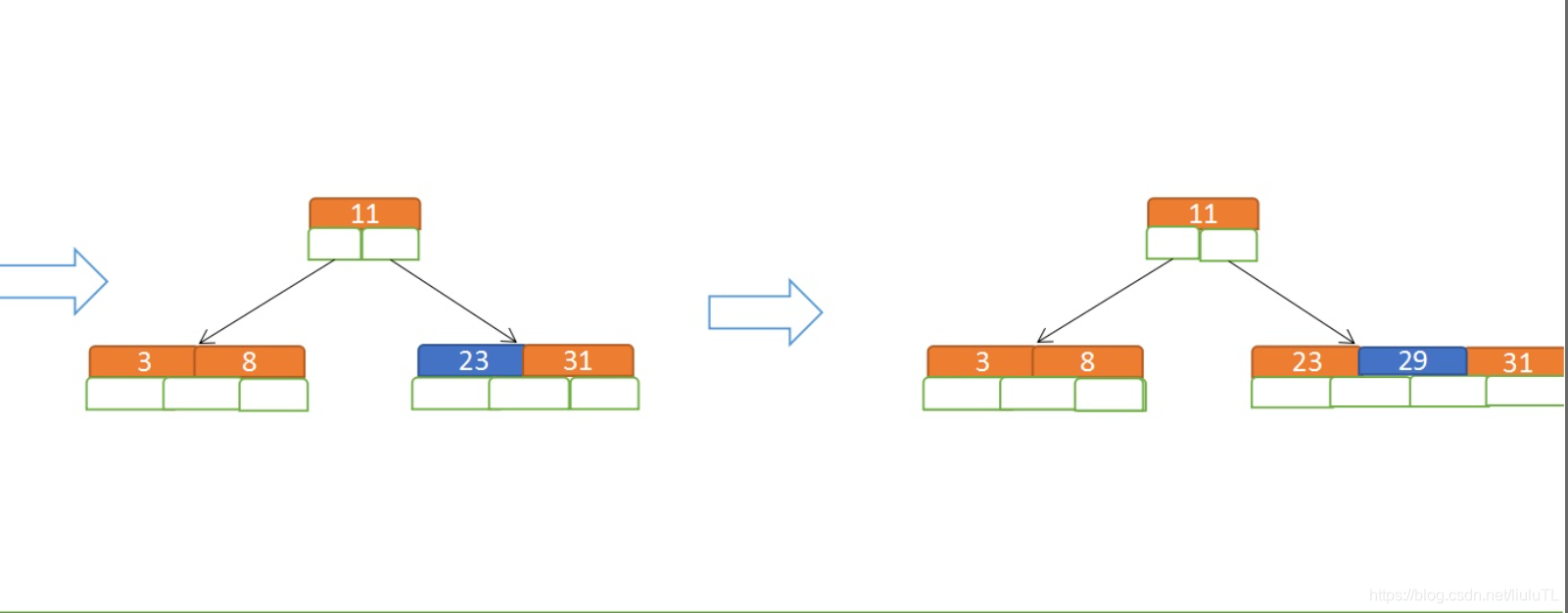
再插入50、28
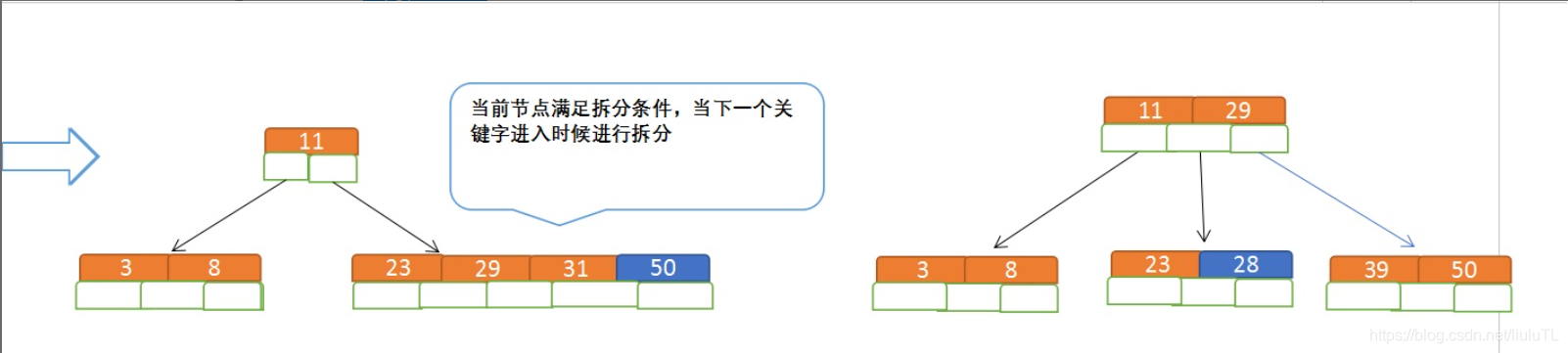
下面是一个4阶B树的生成

B树的删除
-
删除过程中需要考虑以下情况:
1、删除的节点存在子树,即删除非叶子节点。
2、删除节点可能会导致当前子树的元素个数小于最小允许的元素个数。 -
删除叶子节点
1、搜索找到需要删除的元素位置。
2、如果是叶子节点,直接删除该节点。
3、删除后,如果出现了子树元素个数小于最小允许的元素个数(ceil(m/2)-1),那么执行“删除后重平衡”对树进行重平衡。 -
删除内部节点
因为内部节点是左右子树的分割值,左子树都比分割值小,右子树都比分割值大。所以我们需要找到一个新的分割值来对左右子树进行重新分配。
1、从左右子树中找到一个新的分割值(不是左子树的最大值,就是右子树的最小值),将其从原子树中删除,并使用该节点代替需要删除的内部节点。
2、前面步骤删除了一个节点,如果该节点所在子树不满足条件了(子树元素个数小于最小允许的元素个数),那么执行“删除后重平衡”对树进行重平衡。 -
删除后重平衡
如果从节点中删除一个元素使其元素个数小于最小值,那么就需要对其进行重新分配,使树达到平衡。通常,重新分配会从一个大于个数最小值的兄弟节点中移动元素,这种操作称之为旋转。如果不存在这样的兄弟节点,那么需要将兄弟节点和该节点进行合并,并导致父节点失去一个元素,因此父节点也可能会出现缺陷,需要重新再平衡,直到缺陷的节点为根节点为止(因为根节点没有最小元素个数的限制)。
具体的步骤如下:
1、如果缺陷节点的右兄弟节点存在,并且节点元素数量大于最小元素个数要求,则进行左旋:
(1) 将缺陷节点和右兄弟节点的共同父节点的分割值复制到缺陷节点的末端。(此时原缺陷节点没有缺陷)
(2) 将右兄弟节点的第一个元素代替原先父节点的分割值。(此时右兄弟节点也没有缺陷)
(3)此时树已经达到平衡状态。
2、如果缺陷节点的左兄弟节点存在,并且节点元素数量大于最小元素个数要求,则进行右旋:
(1)将缺陷节点和左兄弟节点的共同父节点的分割值复制到缺陷节点的末端。(此时原缺陷节点没有缺陷)
(2) 将左兄弟节点的第一个元素(我觉得应该是左子树的最大值)代替原先父节点的分割值。(此时左兄弟节点也没有缺陷)
(3)此时树已经达到平衡状态。
3、如果缺陷节点的左右兄弟节点都只有最小的元素个数,那么进行合并,并将他们的共同父节点的分割值取出来:
(1)将分割值放在左子树的末端。(左子树有可能是缺陷节点,也有可能是拥有最小元素个数的节点)
(2) 将右子树的所有节点移动到左子树上。(此时左子树拥有最大元素个数,右子树为空)
(3)将分割值和右子树删除,此时父节点失去一个值。
1). 如果父节点是根节点,且现在该节点为空,则释放它,使合并后的节点成为根节点。
2). 如果父节点元素个数小于最小元素个数,那么需要对父节点进行重平衡。
下面的例子中以5阶B树为例,介绍B树的删除操作,5阶B树中,结点最多有4个key,最少有2个key
1、原始状态

2、在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束。

3、在上述情况下接着删除27。从上图可知27位于非叶子结点中,所以用27的后继替换它(不是左子树的最大值,就是右子树的最小值,都可以)。从图中可以看出,27的后继为28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示。

删除后发现,当前叶子结点的记录的个数小于2,而它的兄弟结点中有3个记录(当前结点还有一个右兄弟,选择右兄弟就会出现合并结点的情况,不论选哪一个都行,只是最后B树的形态会不一样而已),我们可以从兄弟结点中借取一个key。所以父结点中的28下移,兄弟结点中的26上移,删除结束。结果如下图所示。(右旋)

4、在上述情况下接着删除32,结果如下图。
此时需要重新平衡,因为兄弟节点没有符合的,所以找爸爸要key后, 将右子树的所有节点移动到左子树上。(此时左子树拥有最大元素个数,右子树为空)
(当删除后,当前结点中只key,而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并,成为一个新的结点,当前结点的指针指向父结点。结果如下图所示。)
5、上述情况下,我们接着删除key为40的记录,删除后结果如下图所示。

同理,当前结点的记录数小于2,兄弟结点中没有多余key,所以父结点中的key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)结点合并,合并后的指向当前结点的指针就指向了父结点。

同理,对于当前结点而言只能继续合并了,最后结果如下所示。

B+树
B+树有很多的好处,磁盘相关的文件存储大部分都会选择B+树进行存储方式。B+树会被当做存储的索引,MySQL,Oracle,DB2等。对于在文件系统和数据库中都如此重要的结构,我们需要仔细的研究一下他的定义、插入和删除。
定义
B+树的定义与B树非常相似:
1、每个节点的孩子数量都比他的元素数量要多一个
2、所有的叶子节点与root节点的路径长度都一致
3、所有节点关键字是按递增次序排列,并遵循左小右大原则
4、根节点至少有两个孩子
5、每一个非叶子结点,非根节点有至少floor(m/2)个子树(m为阶数,向下取整);m阶B+树表示了内部结点最多有m-1个关键字(或者说内部结点最多有m个子树),阶数m同时限制了叶子结点最多存储m-1个记录
6、每一个叶子节点拥有至少floor(m/2)个元素
B+树包含2种类型的结点:内部结点(也称索引结点)和叶子结点。根结点本身即可以是内部结点,也可以是叶子结点。根结点的关键字个数最少可以只有1个
- 与B+树的区别在哪里?
1、B+树的所有数据都是在叶子节点上—内部结点不保存数据,只用于索引,所有数据(或者说记录)都保存在叶子结点中。
2、B+树的叶子节点的指针都会指向下一个叶子节点,像是一条链表一样
3、关键字的个数B+树用的是向下取整

插入操作
1)若为空树,创建一个叶子结点,然后将记录插入其中,此时这个叶子结点也是根结点,插入操作结束。
2)针对叶子类型结点:根据key值找到叶子结点,向这个叶子结点插入记录。插入后,若当前结点key的个数小于等于m-1,则插入结束。否则将这个叶子结点分裂成左右两个叶子结点,左叶子结点包含前m/2个记录,右结点包含剩下的记录,将第m/2+1个记录的key进位到父结点中(父结点一定是索引类型结点),进位到父结点的key左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第3步。
3)针对索引类型结点:若当前结点key的个数小于等于m-1,则插入结束。否则,将这个索引类型结点分裂成两个索引结点,左索引结点包含前(m-1)/2个key,右结点包含m-(m-1)/2个key,将第m/2个key进位到父结点中,进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。将当前结点的指针指向父结点,然后重复第3步。
下面是一颗5阶B树的插入过程,5阶B数的结点最少(floor(5/2))2个key,最多4个key。

插入16后超过了关键字的个数限制,所以要进行分裂。在叶子结点分裂时,分裂出来的左结点2个记录,右边3个记录,中间key成为索引结点中的key,分裂后当前结点指向了父结点(根结点)。结果如下图所示

当然我们还有另一种分裂方式,给左结点3个记录,右结点2个记录,此时索引结点中的key就变为15。

当前结点的关键字个数大于5,进行分裂。分裂成两个结点,左结点2个记录,右结点3个记录,关键字16进位到父结点(索引类型)中,将当前结点的指针指向父结点。
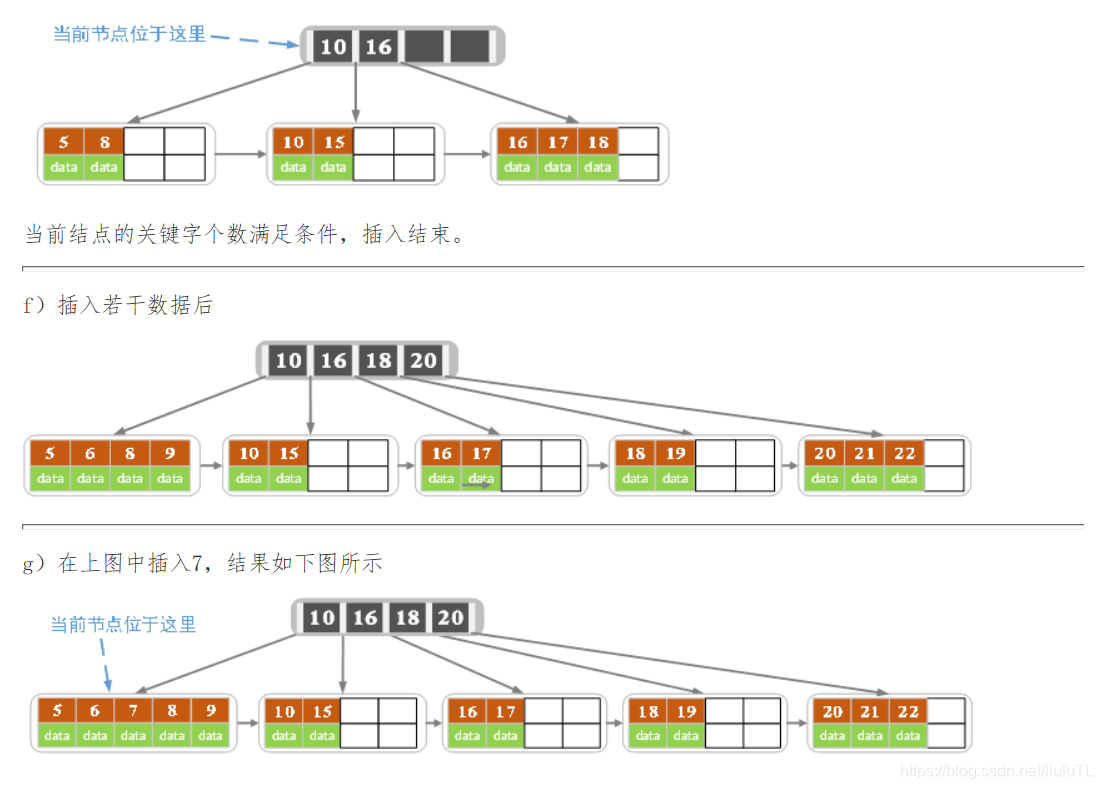
当前结点的关键字个数超过4,需要分裂。左结点2个记录,右结点3个记录。分裂后关键字7进入到父结点中,将当前结点的指针指向父结点,结果如下图所示。

当前结点的关键字个数超过4,需要继续分裂。左结点2个关键字,右结点2个关键字,关键字16进入到父结点中,将当前结点指向父结点,结果如下图所示。

当前结点的关键字个数满足条件,插入结束。
删除操作
如果叶子结点中没有相应的key,则删除失败。否则执行下面的步骤
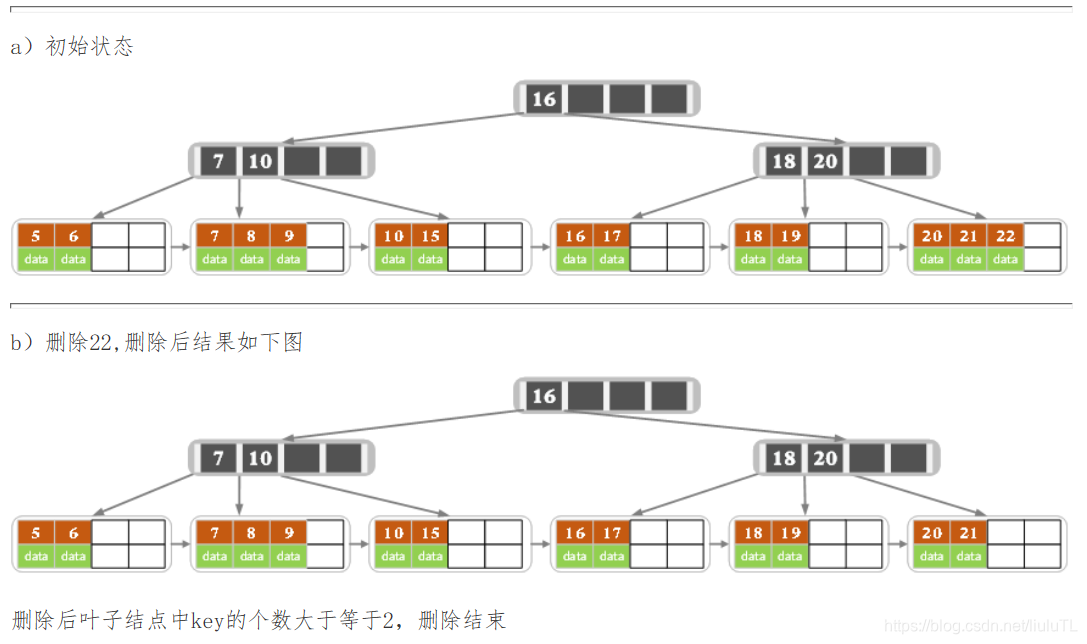
1)删除叶子结点中对应的key。删除后若结点的key的个数大于等于大于Math.ceil(m/2) – 1,删除操作结束,否则执行第2步。
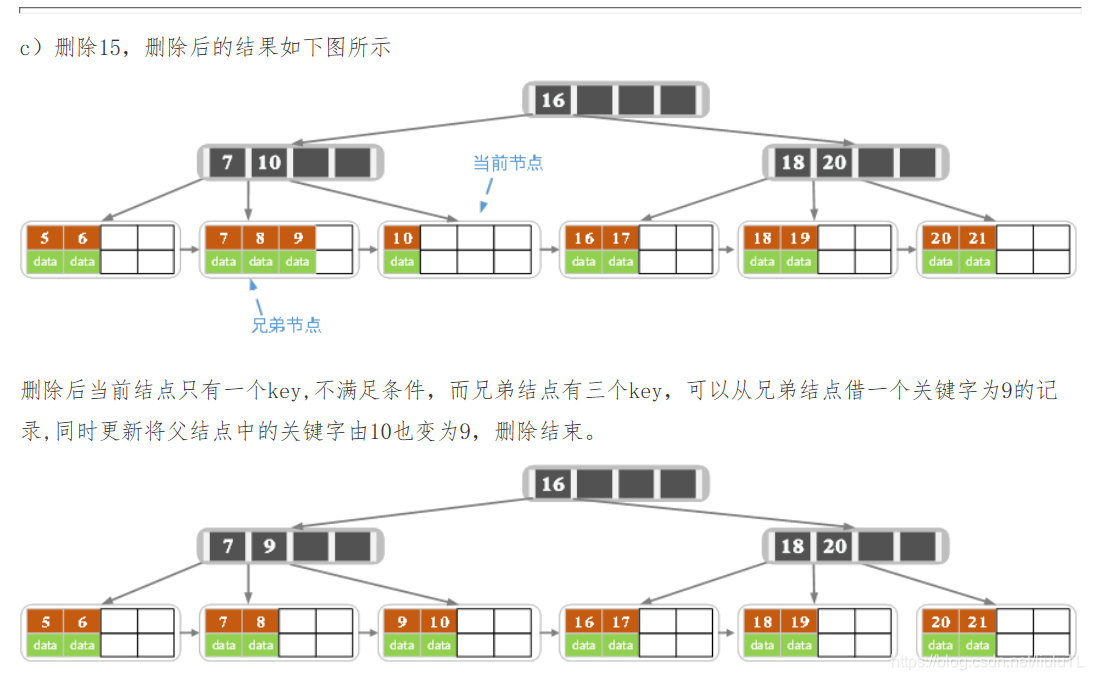
2)若兄弟结点key有富余(大于Math.ceil(m/2) – 1),向兄弟结点借一个记录,同时用借到的key替换父结(指当前结点和兄弟结点共同的父结点)点中的key,删除结束。否则执行第3步。
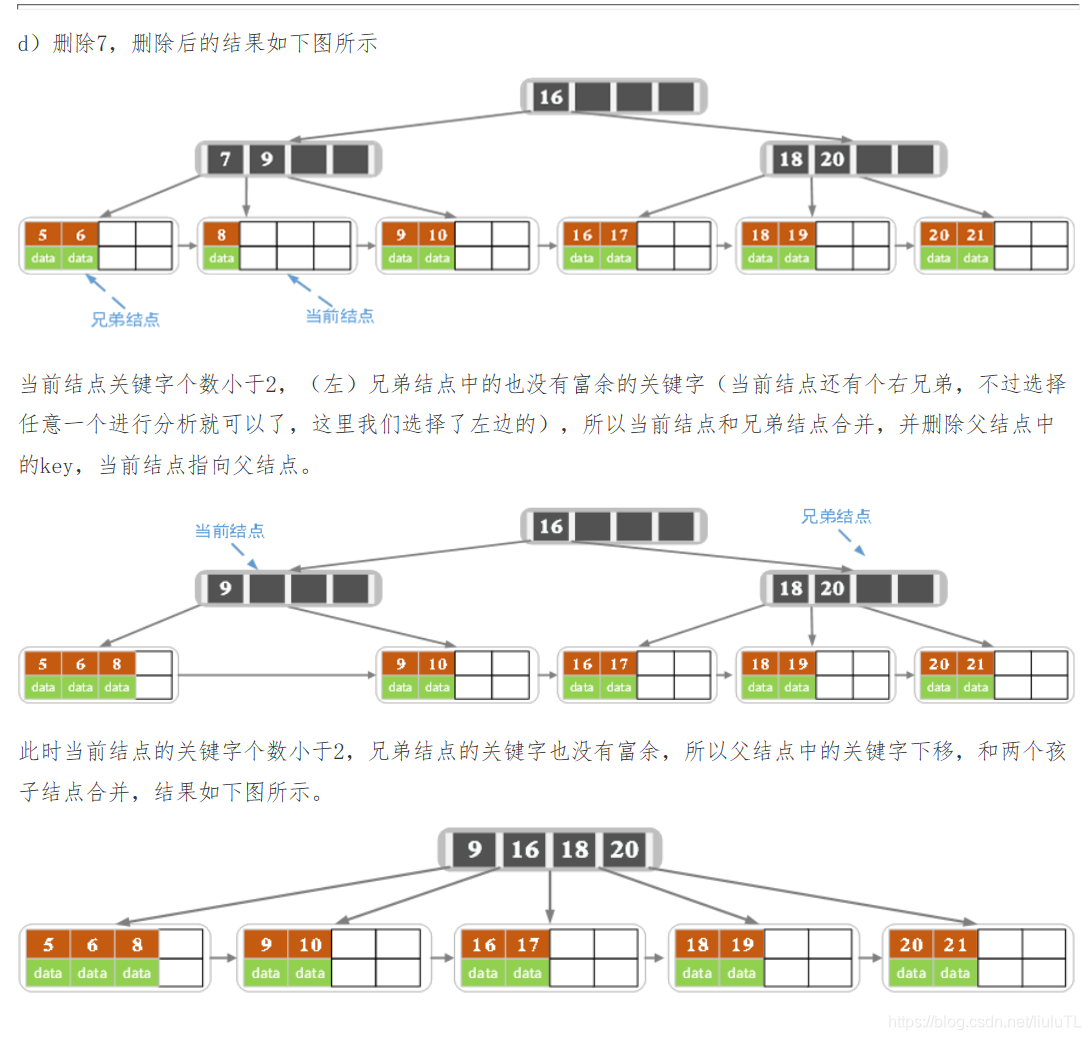
3)若兄弟结点中没有富余的key,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的key(父结点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第4步(第4步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
4)若索引结点的key的个数大于等于大于Math.ceil(m/2) – 1,则删除操作结束。否则执行第5步
5)若兄弟结点有富余,父结点key下移,兄弟结点key上移,删除结束。否则执行第6步
6)当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点,重复第4步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。
下面是一颗5阶B树的删除过程,5阶B数的结点最少2个key,最多4个key。
参考:https://www.cnblogs.com/nullzx/p/8729425.html
