算法导论------渐近记号Θ、Ο、o、Ω、ω详解

1.渐近精确界记号： Θ （big-theta）

假设算法A的运行时间表达式 T1(n) 为： T1(n)=30n4+20n3+40n2+46n+100
假设算法B的运行时间表达式 T2(n) 为： T2(n)=1000n3+50n2+78n+10
当问题规模足够大的时候，例如n=100万，算法的运行时间将主要取决于时间表达式的第一项，其它项的执行时间只有它的几十万分之一，可以忽略不计。第一项的常数系数，随着n的增大，对算法的执行时间也变得不重要了。
于是，算法A的运行时间可以记为： T1(n)≈n4 ，记为 T1(n)=Θ(n4) ；算法B的运行时间可以记为： T2(n)≈n4 ，记为 T2(n)=Θ(n4) 。

Θ 的数学含义
方式一：设 f(n) 和 g(n) 是定义域为自然数集合的函数。如果 limn→∞f(n)g(n) 存在，并且等于某个常数 c(c>0) ，那么 f(n)=Θ(g(n)) 。通俗理解为 f(n)和g(n) 同阶， Θ 用来表示算法的精确阶。

方式二： Θ(g(n)) ={ f(n) :存在正常量 c1、c2和n0 ，使得对所有 n≥n0 ，有 0≤c1g(n)≤f(n)≤c2g(n) }若存在正常量 c1、c2 ，使得对于足够大的n，函数 f(n) 能“夹入” c1g(n)与c2g(n) 之间，则 f(n) 属于集合 Θ(g(n)) ，记作 f(n)∈Θ(g(n)) 。作为代替，我们通常记“ f(n)=Θ(g(n)) ”。

由下图中左侧 f(n)=Θ(g(n)) 图可以看出，对所有 n>n0 时，函数 f(n) 乘一个常量因子可等于 g(n) ，我们称 g(n) 是 f(n) 的一个渐近紧确界。 Θ 记号在五个记号中，要求是最严格的，因为 g(n) 即可以表示上界也可以表示下界。

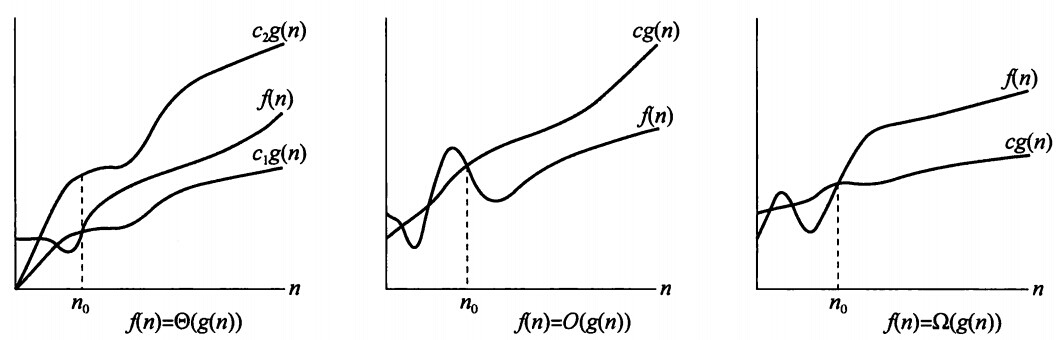
需要注意的是： Θ(g(n)) 的定义要求每个成员 f(n)∈Θ(g(n)) 均渐近非负，即当n足够大时， f(n) 非负。渐近正函数就是对所有足够大的n均为正的函数。

2.渐近上界记号： O (big-oh)

定义：设 f(n)和g(n) 是定义域为自然数集 N 上的函数。若存在正数 c和n0 ，使得对一切 n≥n0 都有 0≤f(n)≤cg(n) 成立，则称 f(n) 的渐进的上界是 g(n) ，记作 f(n)=O(g(n)) 。通俗的说n满足一定条件范围内，函数 f(n) 的阶不高于函数 g(n) 。

根据符号 O 的定义，用它评估算法的复杂度得到的只是问题规模充分大时的一个上界。这个上界的阶越低，评估越精确，越有价值。

例如：设 f(n)=n2+n ,则
f(n)=O(n2) ，取 c=2 , n0=1 即可
f(n)=O(n3) ，取 c=1 , n0=2 即可。显然， O(n2) 作为上界更为精确。

几种常见的复杂度关系

O(1)<O(log(n))<O(n)<O(nlogn)< O(n2)<O(2n)<O(n!)<O(nn)
需要注意的是：对数函数在没有底数时，默认底数为2；如 lgn=logn=log2n 因为计算机中很多程序是用二分法实现的。

符号用法测试：素数测试

int isprime(int n) {
    for(int i=2; i<=(int)sqrt(n); i++) {
        if(n%i==0) { 
            return0;
        }
    }
    return1;
}
  
  
   
   1
   
   2
   
   3
   
   4
   
   5
   
   6
   
   7
   
   8

在上面这个素数测试的例子中，基本运算是整除；时间复杂度 T(n)=O(n12) 是正确的。当被测的数n为偶数时，基本运算一次也没执行，所以 T(n)=Θ(n12) 是错误的，因为没有办法证明 T(n) 的下界是 Ω(n12) 。

3.渐近下界记号： Ω (big-omege)

定义：设 f(n)和g(n) 是定义域为自然数集 N 上的函数。若存在正数 c和n0 ，使得对一切 n≥n0 都有 0≤cg(n)≤f(n) 成立，则称 f(n) 的渐进的下界是 g(n) ，记作 f(n)=Ω(g(n)) 。通俗的说n满足一定条件范围内，函数 f(n) 的阶不低于函数 g(n) 。

根据符号 Ω 的定义，用它评估算法的复杂度得到的只是问题规模充分大时的一个下界。这个下界的阶越高，评估越精确，越有价值。

例如：设 f(n)=n2+n ,则
f(n)=Ω(n2) ，取 c=1 , n0=1 即可
f(n)=Ω(100n) ，取 c=1/100 , n0=1 即可

显然， Ω(n2) 作为下界更为精确。

4.非渐近紧确上界：o(小-oh)

定义1：设 f(n)和g(n) 是定义域为自然数集 N 上的函数。若对于任意正数 c，都存在n0 ，使得对一切 n≥n0 都有 0≤f(n)<cg(n) 成立，则称 f(n) 的渐进的非紧确上界是 g(n) ，记作 f(n)=o(g(n)) 。通俗的说n满足一定条件范围内，函数 f(n) 的阶低于函数 g(n) 。
定义2：设 f(n) 和 g(n) 是定义域为自然数集合的函数。如果 limn→∞f(n)g(n)=0 ，那么 f(n)=o(g(n)) 。通俗理解为 f(n)低于g(n) 的阶。

由 O 记号提供的渐近上界可能是渐近紧确的，也可能是非紧确的。（如： 2n2=O(n2) 是渐近紧确的，而 2n=O(n2) 是非紧确上界。）
例子： f(n)=n2+n ，则 f(n)=o(n3)

5.非渐近紧确下界：ω(小-omege)

定义1：设 f(n)和g(n) 是定义域为自然数集 N 上的函数。若对于任意正数 c，都存在n0 ，使得对一切 n≥n0 都有 0≤cg(n)<f(n) 成立，则称 f(n) 的渐进的非紧确下界是 g(n) ，记作 f(n)=ω(g(n)) 。通俗的说n满足一定条件范围内，函数 f(n) 的阶高于函数 g(n) 。
定义2：设 f(n) 和 g(n) 是定义域为自然数集合的函数。如果 limn→∞f(n)g(n)=∞ ，那么 f(n)=o(g(n)) 。通俗理解为 f(n)高于g(n) 的阶。

ω 记号与 Ω 的关系类似于 o和O 记号的关系。我们用 ω 表示一个非渐近紧确的下界。
例子： f(n)=n2+n ，则 f(n)=ω(n) 是正确的。 f(n)=ω(n2) 则是错误的， f(n)=Ω(n2) 是正确的。

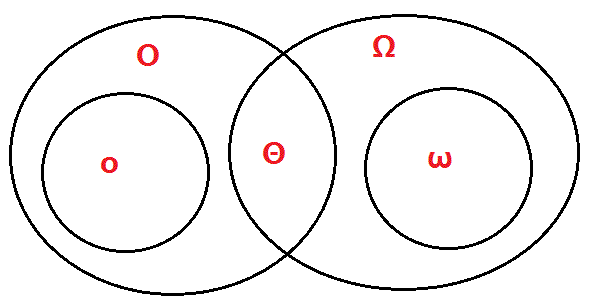
6.渐近记号Θ、Ο、o、Ω、ω关系

记号	含义	通俗理解
(1)Θ（西塔）	紧确界。	相当于”=”
(2)O （大欧）	上界。	相当于”<=”
(3)o（小欧）	非紧的上界。	相当于”<”
(4)Ω（大欧米伽）	下界。	相当于”>=”
(5)ω（小欧米伽）	非紧的下界。	相当于”>”