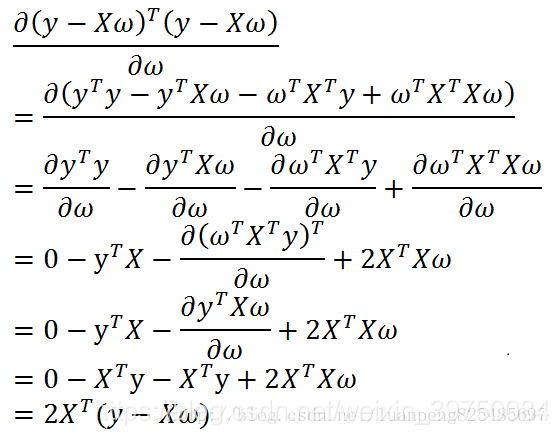线性回归详细推导

（作者：陈玓玏）

假设有一组数据 $X$，包含 $m$个样本，其中每一个样本有 $n$个特征值，每一个样本还对应其label $y_i$，也就是说这组数据是一个 $m*n$的矩阵，那么我们可以通过一组参数 $\theta$来实现对label的预测，这样当新来一个样本时，我们可以通过找到的这一组参数 $\theta$和样本的运算（实际是一个函数）来预测其 $y$值。

1. 代价函数

那怎么评估我们的预测是否准确呢？

先来科普一个三个概念：
  损失函数（Loss Function）：是定义在单个样本上的，是指一个样本的误差。
  代价函数（Cost Function）：是定义在整个训练集上的，是所有样本误差的平均，也就是所有损失函数值的平均。
  目标函数（Object Function）：是指最终需要优化的函数，一般来说是经验风险+结构风险，也就是（代价函数+正则化项）。

基于以上的概念，再加上线性回归的损失函数是平方损失函数，最终得到的代价函数公式为：
$J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)}^2$
$h_\theta(x^i)$表示第 $i$个样本的预测值，其公式为 $h_\theta(x^{i})=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_mx_m$， $y^i$表示第 $i$个样本的真实值。 $\theta_0$是截距项，可以理解为样本矩阵有一列全为1，这一列的系数是 $\theta_0$。

我们拟合的目标是使得代价函数最小，表示每个样本预测值与真实值之间的差距平均值最小。既然样本值是确定的，那么我们要找的就是使得代价函数最小的一组 $\theta$值，考虑一个足够简单的场景，即所有样本只有一个特征且 $\theta_0$为0。此时我们可以知道，代价函数转换为以下形式：
$J(\theta_1) =\frac{1}{2m}\sum_{i=1}^{m} (\theta_1x^i-y^i)^2$
这个函数只有一个参数 $\theta_1$，且展开平方项的系数必然大于0，因此和项中的每一项都是一个自变量为 $\theta_1$的开口向上的抛物线， $m$项的和仍然是一个开口向上的抛物线，因此我们总能找到一个使得 $J(\theta_1)$最小的 $\theta_1$。扩展到多参数以后仍然成立。

2. 最小二乘法及梯度下降法

2.1 求解及更新参数

那么如何求解 $\theta$向量呢？
有两种方法可以考虑，一种是最小二乘法，一种是梯度下降法。两者的原理其实是一样的，那就是当 $J(\theta)$对 $\theta$的偏导为0时，所得到的 $\theta$值即为我们要求的结果。但最小二乘法是将整个代价函数转化为向量相乘的结果整体求解，

这里的 $\omega$就是我们说的 $\theta$，求解的结果为
$\theta = (X^TX)^{-1}X^TY$
这个结果求解的困难之处在于求逆。矩阵无法求逆的原因在于存在多余的特征（因为共线性），会导致 $X^TX$的行列式为0，因而不能求导。此时应该去分析各特征之间的共线性情况，相关性极高的特征群中留一个就可以了。

因为最小二乘法在存在共线性特征时无法求解，且在特征多时求解很慢（毕竟需要求一个 $(n+1)*(n+1)$矩阵的逆），所以我们通常喜欢用另一种方法来求解，即梯度下降法。
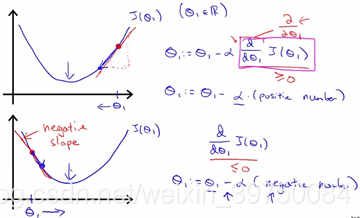
梯度下降法的原理是沿着梯度下降的方向逐步逼近最低点。下面来看一张图：

当前处于极值点左边时，梯度为负值，参数需要往增大的方向变化，因此我们更新参数时需要用当前参数值减去一个负数，而处于极值点右边时，梯度为正，参数需要往减小的方向变化，也是要减去一个正数，总之就是越来越接近极小值点。

也就是说，我们只需要按照梯度下降的方向（也就是 $J(\theta)$在 $\theta_i$上下降最快的方向）每次跨出一小步，经过多次前进之后我们总能到达一个最近的极小值。
梯度可以由以下公式求得：
$\frac{\partial J(\theta)}{\partial \theta_0} = \frac{1}{m}\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)}$
$\frac{\partial J(\theta)}{\partial \theta_i} = \frac{1}{m}\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)}x^i$

而梯度更新的方式为：
$\theta_i = \theta_i-\alpha \frac{\partial J(\theta)}{\partial \theta_i}$
即：
$\theta_0 = \alpha \frac{1}{m}\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)}$
$\theta_i = \alpha \frac{1}{m}\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)}x^i$

2.2 学习率的选择

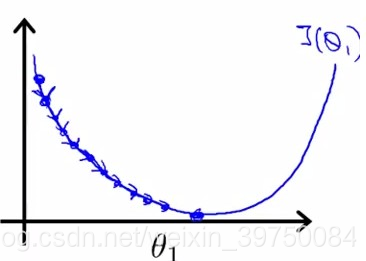
那么在以上公式中，还有一个疑惑就是， $\alpha$参数是什么？这个参数就是步长，又称学习率，它能够控制我们学习的速度，具体看下图：

当学习率很小时，我们每次只会随着梯度的方向往前前进一点点，需要更多的迭代次数才能到达极小值点，找到合适的参数。当学习率很大时，每次更新的长度过大导致越过极值点，容易走成之字形，难以收敛，所以要将学习率控制在合理范围内，可以从一个较小的值开始尝试，逐步增大到合适的大小。

2.3 特征归一化

除了学习率，另外一个值得注意的问题就是特征归一化。看图说话：

左图是未归一化的代价函数等高线图（也就是不同的 $J(\theta)$值的横截面边缘，因为两个参数的 $J(\theta)$是抛物面，因此是这个形状），右图是归一化之后的。归一化简单来说就是将各个特征缩放到同一个scale上，如果不进行这个操作，容易出现左图的情况，也就是说 $J(\theta)$在scale较小的 $x_2$对应的参数 $\theta_2$上的每一步都是在逐渐减小的，但scale较大的 $x_1$对应的参数 $\theta_1$每次下降时，梯度公式中是包含数值较大的 $x_1^i$的（可以自己推导一下），这样即使步长小， $\theta_1$也容易因为过度更新而产生过学习。

所以我们需要进行归一化，以期学习过程能够像右图那样进行。

参考文献：

1. https://blog.csdn.net/abcjennifer/article/details/7691571
2. https://blog.csdn.net/abcjennifer/article/details/7700772
3. https://blog.csdn.net/luanpeng825485697/article/details/78933084