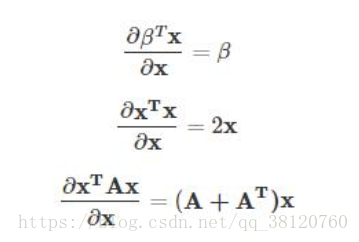线性回归数学推导

线性回归的目标是确定一条直线，让所有样本点到这一条直线的距离之和最小。通过这一句话我们就可以自然而然地根据样本点列出目标函数

现在我们有一组高维样本点 $(X_{1},y_{1}),(X_{2},y_{2}),(X_{3},y_{3}),(X_{4},y_{4}),.......,(X_{n},y_{n})$ （其中每一个x都是m维列向量）。

我们设目标直线方程为 y = $\omega _{0}*1+\omega _{1}*x_{1}+\omega _{2}*x_{2}+\omega _{3}*x_{3}+.......\omega _{n}*x_{n}$ （这个等式里面全是单个数字没有向量）

把这个方程写作向量的形式 y = $W^{T}X$ （其中X是m+1维的列向量，W也是）

$D = \sum_{i=1}^{n}(W^{T}X_{i}-y_{i})^2$ (对于 $X_{i}$ 是在每一个n维样本点的首位补充了一个1形成的m+1维的向量) 这个式子表示n个样本点到目标直线的距离之和。此处的方程就是线性回归的损失函数。

接下来我们就要最小化损失函数来求取未知量 W 对于方程 $D = \sum_{i=1}^{n}(W^{T}X_{i}-y_{i})^2$ 我们可以得知他存在一个全局最小值（具体证明请自行百度）

所以方程导数为0处必定是全局最小值处。可以得到等式 $\frac{\partial D}{\partial W} = 0$ 下面对方程进行变换

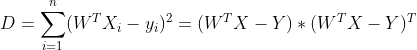
$D = \sum_{i=1}^{n}(W^{T}X_{i}-y_{i})^2 = (W^{T}X-Y)*(W^{T}X-Y)^{T}$

（其中的X为（m+1）*n的矩阵。 $X = \begin{pmatrix} 1&1 & 1 & 1 & 1\\ x_{11}& x_{21}&x_{31} &... & x_{n1}\\ x_{12}& x_{22}& x_{32} & ... & x_{n2}\\ x_{13}& x_{23}& x_{33}& ... & x_{n3}\\ ...& ... & ... & ... & ...\\ x_{1m}& x_{2m} & x_{3m} & ...&x_{nm} \end{pmatrix}$ 每一列为一个样本。 $Y = \begin{pmatrix} y_{1} & y_{2} &y_{3} & ... & y_{n} \end{pmatrix}$ ）

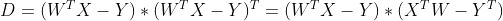
$D = (W^{T}X-Y)*(W^{T}X-Y)^{T}= (W^{T}X-Y)*(X^{T}W-Y^{T})$

~~$= W^{T}XX^{T}W-{\color{Red} W^{T}XY^{T}}-YX^{T}W-YY^{T}$~~

~~$= W^{T}XX^{T}W-2YX^{T}W-YY^{T}$~~ (因为 $W^{T}XY^{T}$ 是一个常数，所以 $W^{T}XY^{T}$ = $(W^{T}XY^{T})^{T}$ = $YX^{T}W$ )

$\frac{\partial D}{\partial W} = 2XX^{T}W-2XY^{T}$ (这里需要用到矩阵求导的知识，下面给出常用的公式)

由    $\frac{\partial D}{\partial W} = 2XX^{T}W-2XY^{T}=0$ 得   $XX^{T}W = XY^{T}$ 则   $W = (XX^{T})^{-1}XY^{T}$

但是这个等式成立的条件是   $XX^{T}$ 必须可逆。即给定的样本集中不能出现重复数据，样本特征数量不能大于所给训练集样本个数。

利用最大似然估计推导出损失函数

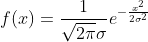
首先给定一个先验假设，样本真实值与预测值的差值服从 $N(0,\sigma^{2})$   的正态分布    $f(x) = \frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{x^{2}}{2\sigma ^{2}}}$

对于连续性随机变量，其在某一点处的概率可以表示为 $p(x) = f(x)*dx$   (f(x) 为随机变量的概率密度函数 dx代表x轴上的微分)

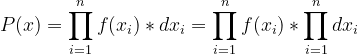
所以样本的联合概率为    $P(x) = \prod_{i=1}^{n}f(x_{i})*dx_{i}= \prod_{i=1}^{n}f(x_{i})*\prod_{i=1}^{n}dx_{i}$

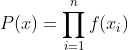
由于    $\prod_{i=1}^{n}dx_{i}$   近似常量，所以对于 P(x) 求极值没有影响。所以可以写作    $P(x) = \prod_{i=1}^{n}f(x_{i})$

$l(\theta ) =\prod_{i=1}^{n} \frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{(W^{T}X_{i}-y_{i})^{2}}{2\sigma ^{2}}}$

$arg\, \underset{\theta }{max} \, l(\theta ) =arg\, \underset{\theta }{max}\, \: \: ln\prod_{i=1}^{n} \frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{(W^{T}X_{i}-y_{i})^{2}}{2\sigma ^{2}}}$

$=arg\: \underset{\theta }{max}\: \sum_{i=1}^{n}(\frac{-(W^{T}X_{i}-y_{i})^{2}}{2\sigma^{2}}*ln\frac{1}{\sqrt{2\pi }\sigma })$

$=arg\: \underset{\theta }{max}\: \sum_{i=1}^{n}-(W^{T}X_{i}-y_{i})^{2}$ (由于 $ln\frac{1}{\sqrt{2\pi }\sigma }$ 和 $2\sigma ^{2}$ 是常量所以在求 $arg\, \underset{\theta }{max} \, l(\theta )$ 时无影响可以去掉 )

$=arg\: \underset{\theta }{min}\: \sum_{i=1}^{n}(W^{T}X_{i}-y_{i})^{2}$ (此时就得到了上述的损失函数)

线性回归数学推导

猜你喜欢