图(graph)是数据结构和算法学中最强大的框架之一(或许没有之一)。图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。
而要进入图论的世界,清晰、准确的基本概念是必须的前提和基础。下面对其最核心和最重要的概念作出说明。
一、图的基本组成
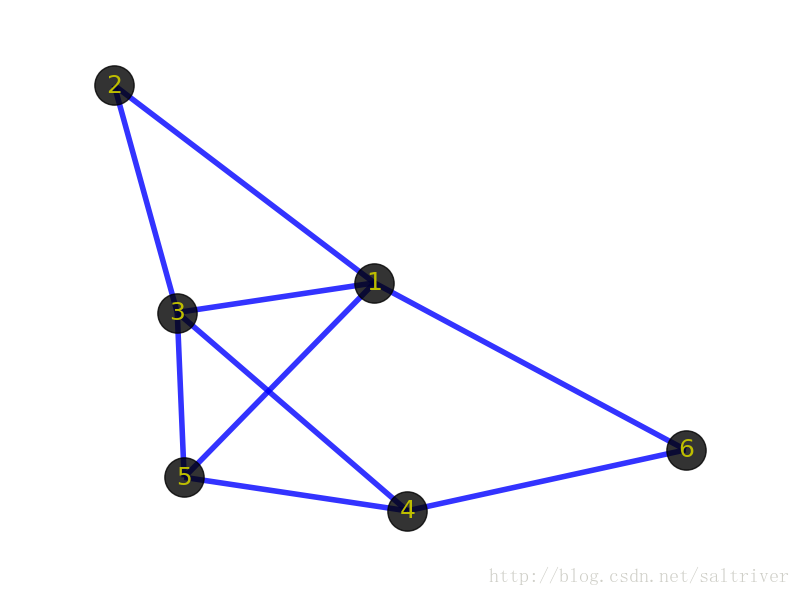
图(graph)并不是指图形图像(image)或地图(map)。通常来说,我们会把图视为一种由“顶点”组成的抽象网络,网络中的各顶点可以通过“边”实现彼此的连接,表示两顶点有关联。注意上面图定义中的两个关键字,由此得到我们最基础最基本的2个概念,顶点(vertex)和边(edge)。
1.1、顶点(vertex)
上图中黑色的带数字的点就是顶点,表示某个事物或对象。由于图的术语没有标准化,因此,称顶点为点、节点、结点、端点等都是可以的。
1.2、边(edge)
上图中顶点之间蓝色的线条就是边,表示事物与事物之间的关系。需要注意的是边表示的是顶点之间的逻辑关系,粗细长短都无所谓的。包括上面的顶点也一样,表示逻辑事物或对象。
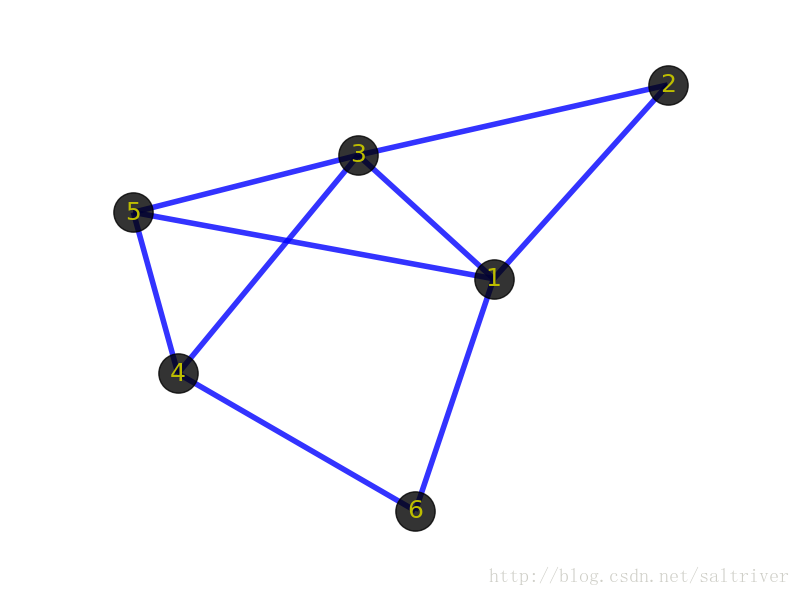
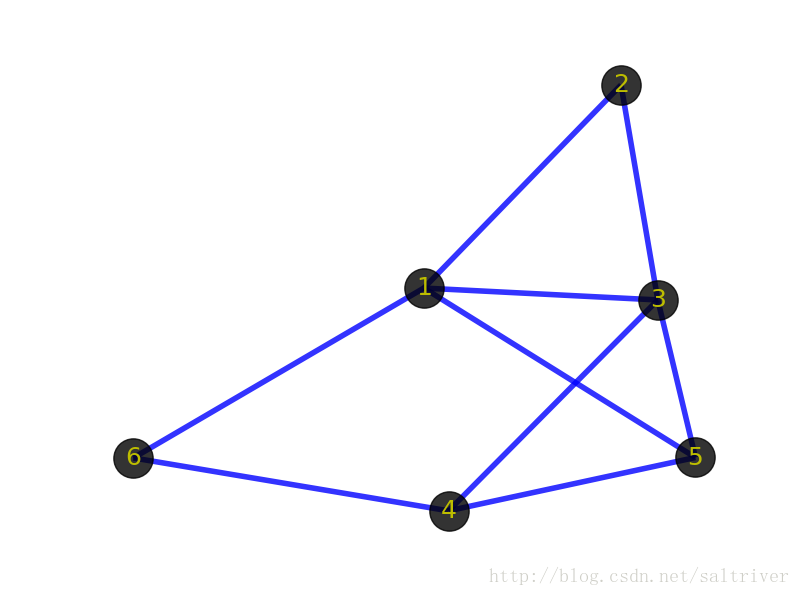
1.3、同构(Isomorphism )
先看看下面2张图:
首先你的感觉是这2个图肯定不一样。但从图(graph)的角度出发,这2个图是一样的,即它们是同构的。前面提到顶点和边指的是事物和事物的逻辑关系,不管顶点的位置在哪,边的粗细长短如何,只要不改变顶点代表的事物本身,不改变顶点之间的逻辑关系,那么就代表这些图拥有相同的信息,是同一个图。同构的图区别仅在于画法不同。
1.4、有向/无向图(Directed Graph/ Undirected Graph)
最基本的图通常被定义为“无向图”,与之对应的则被称为“有向图”。两者唯一的区别在于,有向图中的边是有方向性的。下图即是一个有向图,边的方向分别是:(1->2), (1-> 3), (3-> 1), (1->5), (2->3), (3->4), (3->5), (4->5), (1->6), (4->6)。要注意,图中的边(1->3)和(3->1)是不同的。有向图和无向图的许多原理和算法是相通的。
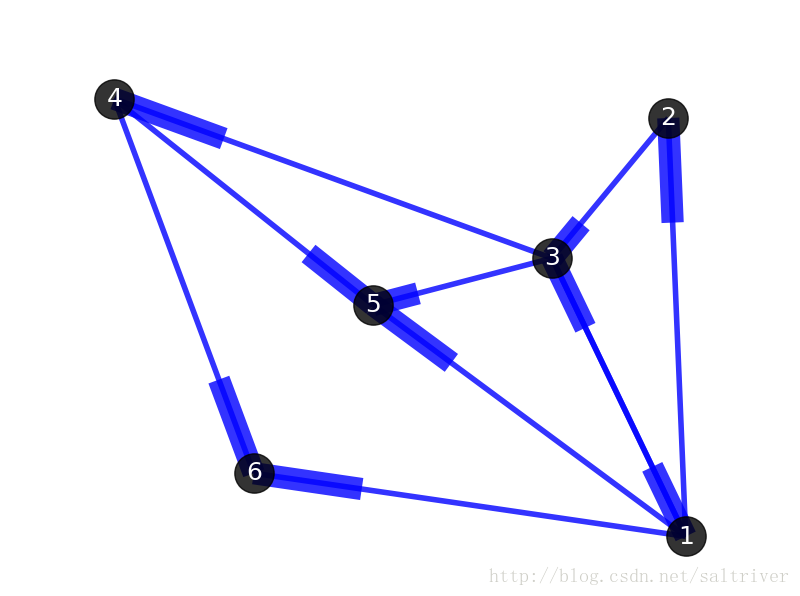
1.5、权重(weight)
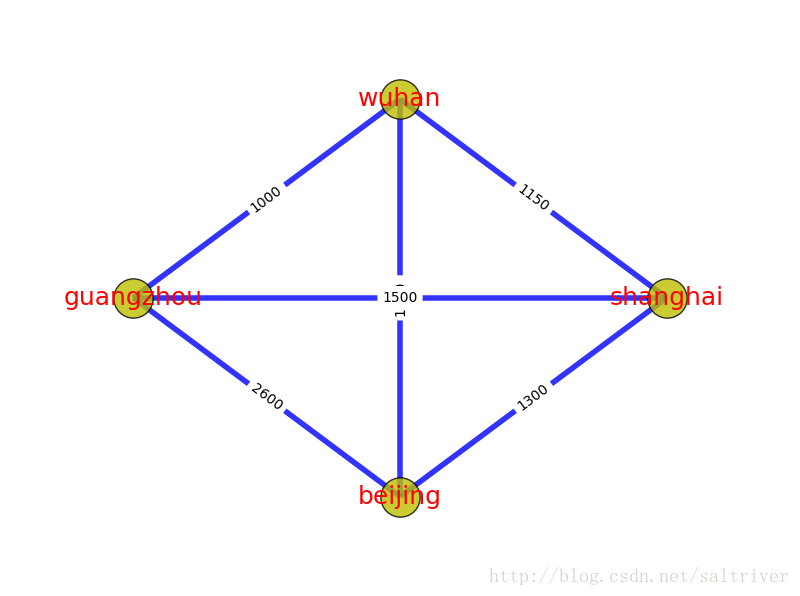
边的权重(或者称为权值、开销、长度等),也是一个非常核心的概念,即每条边都有与之对应的值。例如当顶点代表某些物理地点时,两个顶点间边的权重可以设置为路网中的开车距离。下图中顶点为4个城市:Beijing, Shanghai, Wuhan, Guangzhou,边的权重设置为2城市之间的开车距离。有时候为了应对特殊情况,边的权重可以是零或者负数,也别忘了“图”是用来记录关联的东西,并不是真正的地图。
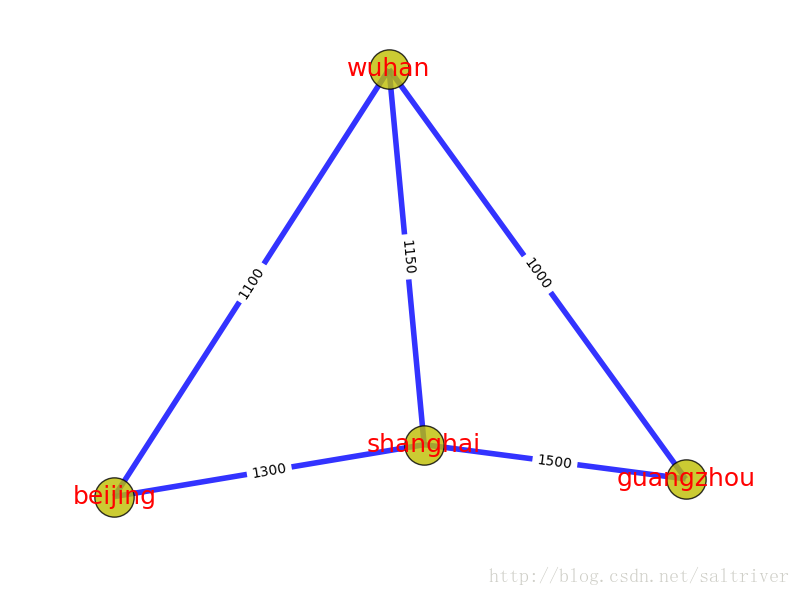
1.6、路径/最短路径(path/shortest path)
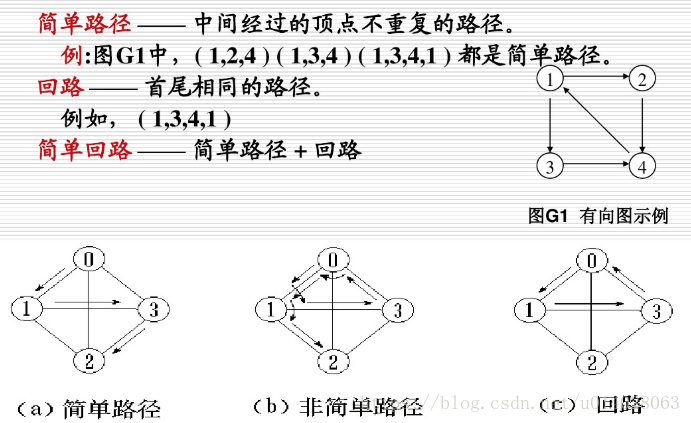
在图上任取两顶点,分别作为起点(start vertex)和终点(end vertex),我们可以规划许多条由起点到终点的路线。不会来来回回绕圈子、不会重复经过同一个点和同一条边的路线,就是一条“路径”。两点之间存在路径,则称这2个顶点是连通的(connected)。
还是上图的例子,北京->上海->广州,是一条路径,北京->武汉->广州,是另一条路径,北京—>武汉->上海->广州,也是一条路径。而北京->武汉->广州这条路径最短,称为最短路径。
路径也有权重。路径经过的每一条边,沿路加权重,权重总和就是路径的权重(通常只加边的权重,而不考虑顶点的权重)。在路网中,路径的权重,可以想象成路径的总长度。在有向图中,路径还必须跟随边的方向。
值得注意的是,一条路径包含了顶点和边,因此路径本身也构成了图结构,只不过是一种特殊的图结构。

1.7、环(loop)
环,也称为环路,是一个与路径相似的概念。在路径的终点添加一条指向起点的边,就构成一条环路。通俗点说就是绕圈。
上图中,北京->上海->武汉->广州->北京,就是一个环路。北京->武汉->上海->北京,也是一个环路。与路径一样,有向图中的环路也必须跟随边的方向。环本身也是一种特殊的图结构。
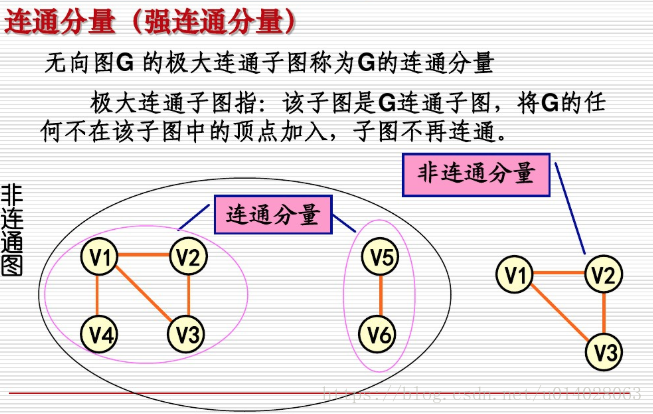
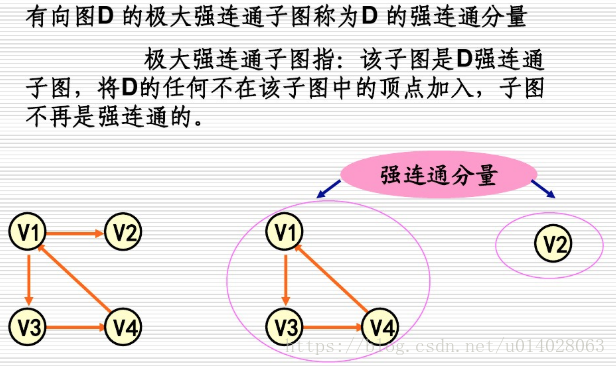
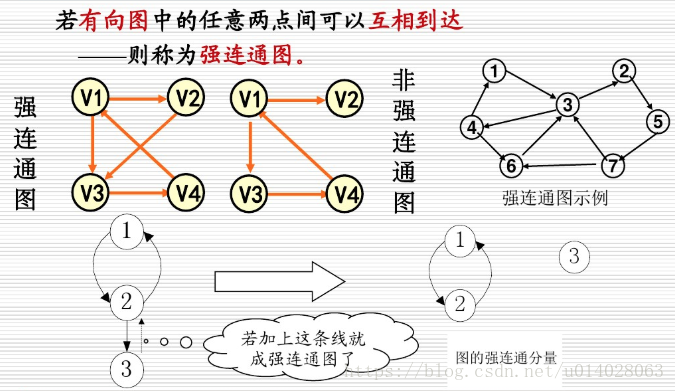
1.8、连通图/连通分量(connected graph/connected component)
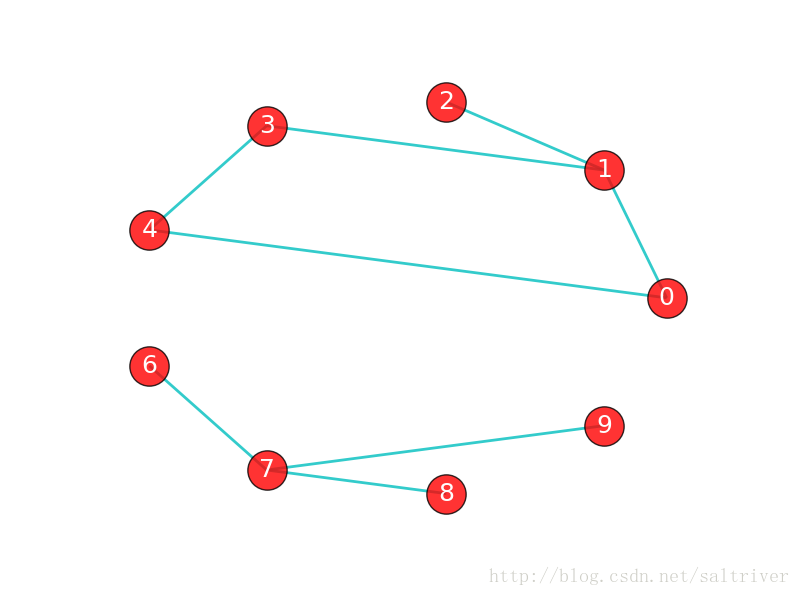
如果在图G中,任意2个顶点之间都存在路径,那么称G为连通图(注意是任意2顶点)。上面那张城市之间的图,每个城市之间都有路径,因此是连通图。而下面这张图中,顶点8和顶点2之间就不存在路径,因此下图不是一个连通图,当然该图中还有很多顶点之间不存在路径。
上图虽然不是一个连通图,但它有多个连通子图:0,1,2顶点构成一个连通子图,0,1,2,3,4顶点构成的子图是连通图,6,7,8,9顶点构成的子图也是连通图,当然还有很多子图。
我们把一个图的最大连通子图称为它的连通分量。0,1,2,3,4顶点构成的子图就是该图的最大连通子图,也就是连通分量。连通分量有如下特点:
1)是子图;
2)子图是连通的;
3)子图含有最大顶点数。
注意:“最大连通子图”指的是无法再扩展了,不能包含更多顶点和边的子图。0,1,2,3,4顶点构成的子图已经无法再扩展了。
显然,对于连通图来说,它的最大连通子图就是其本身,连通分量也是其本身。
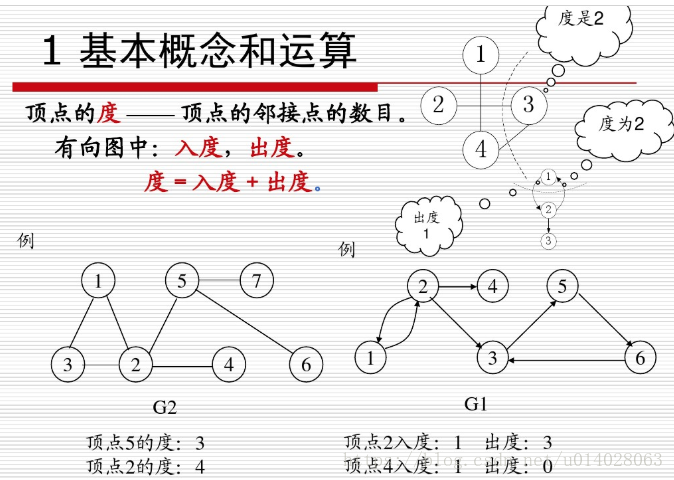
1.9、图的度
1.10、图与树
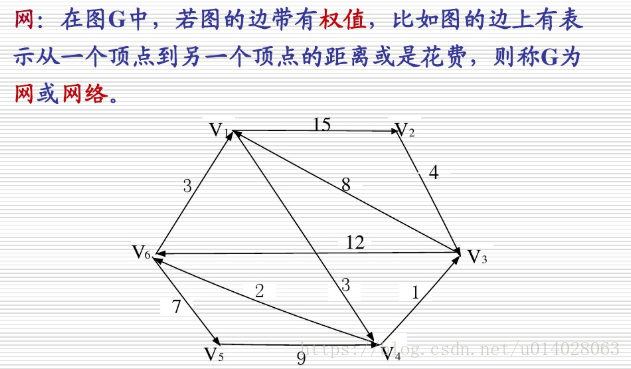
1.11、网
二、图的表示
图的表示即其存储结构除了要存储图中各个顶点本身的信息,还要存储边的信息。
图的存储:图结构在计算机中的存储形式。
常见的图的存储结构有邻接矩阵和邻接表、十字链接表存储方法、邻接多重表存储方法、边集数组,我们重点介绍前两种
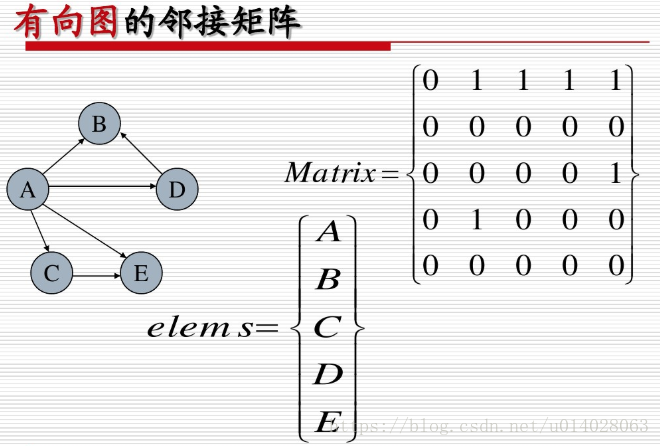
2.1、邻接矩阵表示(数组表示法)
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
邻接矩阵的特点如下:
(1)图的邻接矩阵表示是唯一的;适于存储边的数目较多的稠密图。不带权的有向图的邻接矩阵一般是一个稀疏矩阵。
(2)无向图的邻接矩阵是对称矩阵。压缩方法:存储时只需存储上三角或下三角;
(3)当邻接矩阵是稀疏矩阵时,当图中顶点较多时,可以采用三元组表的方法存储;
(4)对于无向图,邻接矩阵的第i行(或第i列)非零元素的个数正好是第i个顶点的度。
对于有向图,第i行(第i列)非零元素的个数正好是第i个顶点的出度(入度);
(5) 判断两顶点v,u是否为邻接点,只需判断二维数组对应分量是否非零
顶点不变,在图中增加,删除边,只需要对二维数组对应分量复制1(或者权重)或清0
局限性:要确定图中有多少条边,必须按行,按列对每个元素进行检测,花费时间代价很大;
2.2、邻接表
在我们平时使用邻接矩阵的时候经常会遇到以下三种情况:
1. 对于一个|V|很大的图,无法使用邻接矩阵进行存储。对于256M的内存,所以我们最多能使用的|V| = 8192的邻接矩阵。
2. 对于某些稀疏图或者无根树,每个节点都拥有大小为|V|的数组,实际使用很小一部分空间,造成了存储空间上的浪费。
3. 有时两个点之间不止存在有一条边,这是用邻接矩阵就无法同时表示两条以上的边。
由以上情况我们想到了一种特殊的图存储方式,让每个节点拥有的数组大小刚好就等于它所连接的边数。
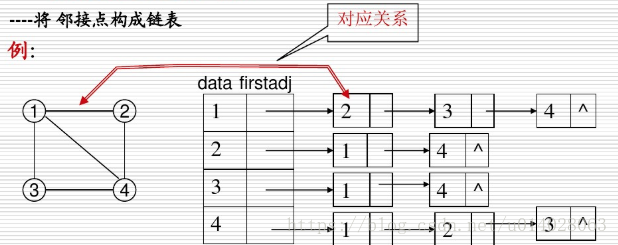
数组与链表相结合的存储方法称为邻接表(Adjacency List)。
具体的处理方法为:
1.图中顶点用一个一维数组存储,当然顶点也可用链表存储,不过数组更方便读取顶点信息。另外,对于顶点数组,每个数据元素还要存储指向第一个邻接点的指针,以便查找顶点的边信息。
2。图中每个顶点 vi 的所有邻接点构成一个线性表,由于邻接点个数不定,所以用单链表存储,无向图称为顶点 vi 的边表,有向图则成为顶点 vi 作为弧尾的出边表。
邻接表的特点如下:
(1)表示不唯一;
(2)对于稀疏图,邻接表比邻接矩阵更省空间;
(3)对于无向图,vi对应第i个链表的表结点个数等于顶点得度;
对于有向图,vi对应第i个链表的表结点个数等于顶点的出度,其入度为邻接表中所有adjvex值域为i的边结点数目。
逆邻接表:就是在有向图的邻接表中,对每个顶点,连接的是指向该顶点的弧。
2.3、十字链接表存储方法
在有向图中,邻接表是有缺陷的,关心了出度问题,要想知道入度,就必须遍历整个图,反之逆邻接表解决了入度却不能解决出度。
十字邻接表是邻接表和逆邻接表的结合,每个边结点对应图中的一条边,把每一条边的边结点分别组织到以起始顶点为头结点的的链表和以终点结点为头结点的链表中。

2.4、 邻接多重表存储方法
邻接多重表(Adjacency Multilist)是无向图的另一中链式存储结构。虽然邻接表是无向图的一种有效的存储结构,在邻接表中容易求顶点和边的各种信息。但是,在邻接表中的每一条边的两个结点分别在不同的链表中。这给某些图的操作带来不便。(如对搜索过的边标记或删除一条边等)邻接多重表的结构和十字链表相似。给每一条边用一个结点表示!
在邻接多重表中,所有依附于同一顶点的边串联在同一链表中,由于每条边依附于两个顶点,则每个边结点同时链接在两个链表中。
可见,对无向图而言,其邻接多重表和邻接表的差别,仅仅在于同一条边在邻接表中用两个结点表示,而在邻接多重表中只有一个结点。
因此,除了在边结点增加一个标志域外,邻接多重表所需的存储量和邻接表相同。因此,各种基本操作的实现亦和邻接表相似。
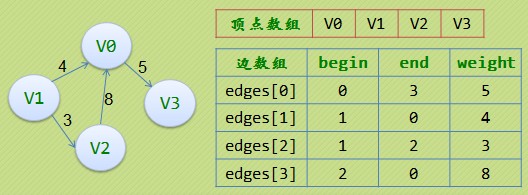
2.5、边集数组
边集数组是由两个一维数组构成。一个是存储顶点的信息;另一个是存储边的信息,这个边数组每个数据元素有一条边的起点下标(begin)、终点下标(end)和权(weight)组成。
边集数组更关注边的集合,查找一丁点的度需要扫描整个边数组,效率不高,因此,其更适合对边依次进行处理的操作。