咕咕咕
很久没写博客了,停课后总结一下DP吧。
声明:本文中题目均来自@DDOSVOID神仙的个人总结题目,禁止转载。侵删。
状压DP
顾名思义,是用将状态进行二进制压缩成集合的形式来方便DP转移的方法。
一些常用的代码表示如下
i & j //取状态i,j重合部分
i ^ j //取状态i,j不同部分
i | j //合并状态i,j
(1 << N) - 1 //表示111…1(N个1)
1 << i - 1 //表示00100…0(1后面有i-1个0,也就是有且仅有二进制下第i位为1)
for (int i = 0; i < n; ++ i) if (x & (1 << i)) cnt++; //统计当前状态x的1的个数
while (x) if (x & 1) ans ++, x >>= 1; //上面的代码也可以这么写 枚举子集
既然是压缩成集合的形式,那么一个不可避免的问题就是如何枚举子集。
假设我们有一个大小为n的集合,那么统计子集数量的代码如下。
for (int S = 1; S < (1 << n); ++ S)
for (int S0 = S; S0; S0 = (S0 - 1) & S)
//do some thing这个东西是NOIP2018提高初赛选择第十题。
具体原理不管了。反正是二进制瞎搞。
简单来说就是,如果要按普通方法枚举子集,应该将S0从S开始每次减一,再判断合法性。然而由于&S的结果只减不增,S0可以通过-1然后&S来直接到达最近合法状态。
有必要分析一下这个代码的时间复杂度。可以看出,只外层一遍循环就是\(O(2^n)\),内层其实是一个组合数\(C_n^k\),那么时间复杂度为\(O(2^nC_n^k)\),又由二项式定理得\(2^nC_n^k=C_n^k1^{n-k}2^n=(2+1)^n\),故时间复杂度为\(O(3^n)\)。
[USACO08NOV]奶牛混合起来Mixed Up Cows
题目描述
Each of Farmer John's N (4 <= N <= 16) cows has a unique serial number S_i (1 <= S_i <= 25,000). The cows are so proud of it that each one now wears her number in a gangsta manner engraved in large letters on a gold plate hung around her ample bovine neck.
Gangsta cows are rebellious and line up to be milked in an order called 'Mixed Up'. A cow order is 'Mixed Up' if the sequence of serial numbers formed by their milking line is such that the serial numbers of every pair of consecutive cows in line differs by more than K (1 <= K <= 3400). For example, if N = 6 and K = 1 then 1, 3, 5, 2, 6, 4 is a 'Mixed Up' lineup but 1, 3, 6, 5, 2, 4 is not (since the consecutive numbers 5 and 6 differ by 1).
How many different ways can N cows be Mixed Up?
For your first 10 submissions, you will be provided with the results of running your program on a part of the actual test data.
POINTS: 200
约翰家有N头奶牛,第i头奶牛的编号是Si,每头奶牛的编号都是唯一的。这些奶牛最近 在闹脾气,为表达不满的情绪,她们在挤奶的时候一定要排成混乱的队伍。在一只混乱的队 伍中,相邻奶牛的编号之差均超过K。比如当K = 1时,1, 3, 5, 2, 6, 4就是一支混乱的队伍, 而1, 3, 6, 5, 2, 4不是,因为6和5只差1。请数一数,有多少种队形是混乱的呢?
输入输出格式
输入格式:
Line 1: Two space-separated integers: N and K
Lines 2..N+1: Line i+1 contains a single integer that is the serial number of cow i: S_i
输出格式:
Line 1: A single integer that is the number of ways that N cows can be 'Mixed Up'. The answer is guaranteed to fit in a 64 bit integer.
输入输出样例
输入样例#1:
4 1
3
4
2
1 输出样例#1:
2 说明
The 2 possible Mixed Up arrangements are:
3 1 4 2
2 4 1 3
状压DP的特点之一就是N特别小,一般最大不会超过23,通常在18附近。题目中的状态通常可以抽象成一段或几段连续的序列,每个元素有两种选择。对于这种状态,通常可以使用状态压缩。
众所周知,2进制数可以看成是一个由0和1组成的序列。我们把2进制数的每一位对应原题目序列的每一个元素,0或1对应该元素选或不选。显然共有\(2^N\)种可能性,当N在较小范围内时,用一个数即可表示当前状态。
在本题中,我们先在最外层for(int i = 0; i <= ((1 << N) - 1); ++ i),表示枚举所有可能的状态,然后for(int j = 1; j <= N; ++ j) if (i & (1 << j - 1))表示当前枚举到的状态i的第j位为1,即选了第j位。这一层循环相当于\(O(N)\)枚举了状态i各位的所有是“1”的状态,即选了的状态。再for(int k = 1; k <= N; ++ k) if (!(i & (1 << k - 1)))与上面类似,这一层循环是对状态的扩展(expand),看看是不是能从当前状态的基础上再多选一个,判断可行的标准是否满足状态i,是否满足题意,T < abs(a[k] - a[j])。如果满足的话,那么当前状态\(dp[i][j]\),表示状态为i时所选的最后一头牛为j的方案数,就可以扩展成\(dp[i|(1<<k-1)][k]\),也就是为状态为i再选上k,最后选的一头牛为k的方案数贡献一份自己的力量(雾)。既得状态转移方程为\(dp[i|(1 << k - 1)][k] += dp[i][j]\)。
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define fr(i, x, n) for(int i=(x);i<=(n);++i)
using namespace std;
typedef long long LL;
const int MAXN = 17;
int N, a[MAXN], K;
LL dp[1 << MAXN][MAXN];
template <typename _Tp>
inline void read(_Tp &x) {
char ch = getchar( ); _Tp f = 1; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar( );
x *= f;
}
int Abs(int x) { return x < 0 ? -x : x; }
int main( ) {
read(N), read(K);
fr(i, 1, N) {
read(a[i]);
dp[1 << i - 1][i] = 1;
}
fr(i, 0, (1 << N) - 1) fr(j, 1, N)
if (i & (1 << j - 1)) fr(k, 1, N)
if (!(i & (1 << k - 1)) && Abs(a[k] - a[j]) > K)
dp[i | (1 << k - 1)][k] += dp[i][j];
LL ans = 0;
fr(i, 1, N) ans += dp[(1 << N) - 1][i];
printf("%lld\n", ans);
return 0;
} 总之……状压DP就是套路啊……
[05]:Cave Cows 1 洞穴里的牛之一
总时间限制: 10000ms
单个测试点时间限制: 1000ms
内存限制: 262144kB
描述
很少人知道其实奶牛非常喜欢到洞穴里面去探险。 洞窟里有N(1≤N≤100)个洞室,由M(1≤M≤1000)条双向通道连接着它们.每对洞室间至多只有一条双向通道.有K(1≤K≤14)个洞室,里面放有1捆干草.牛吃1捆干草,体重指数就会增加1. 贪吃的贝茜要到洞窟里面探险.她希望能吃尽量多的干草,但每条通道有一个宽度阈值,如果体重指数超过相应的阈值,贝茜就会被卡祝她从洞窟1出发,体重指数为0.在洞里溜达一圈后,她要返回洞窟1. 那她最多能吃多少捆干草呢?注意,贝茜经过一个洞室,不一定非要吃掉里面的干草.
输入
第1行输入N,M,K,之后K行每行一个整数,表示在这个洞室放有一捆干草;接下来M行每行三个整数,表示一条双向通道的起点终点和宽度阈值.
输出
最多能吃掉的干草数.
输入输出样例
样例输入
6 7 5
1
2
3
4
5
1 2 3
3 6 2
6 2 10
2 4 1
5 1 1
4 5 1
1 6 1样例输出
4这题没找到地方交……我也不知道代码写的对不对……
由于牛虽然在当前不会被卡,但是不知道下一个洞口是窄是宽,会不会被卡住……
我们可以用Floyd预先处理出两点之间所能达到的最大阙值。然后DP转移就和上一题很像了,只是要特判一下1号洞穴有艹的情况,因为1号洞内的艹显然可以留到最后吃而不用担心被卡住的问题。
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define fr(i, x, n) for(int i=(x);i<=(n);++i)
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXM = 1010;
const int MAXN = 110;
const int MAXK = 15;
int N, M, K, m[MAXN][MAXN];
int dp[1 << MAXK][MAXN], ans, has[MAXN], flag;
template <typename _Tp>
inline void read(_Tp &x) {
char ch = getchar( ); _Tp f = 1; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar( );
x *= f;
}
int Abs(int x) { return x < 0 ? -x : x; }
int main( ) {
read(N), read(M), read(K);
int a, b, c, x;
for (int i = 1; i <= K; ++ i) {
read(has[i]);
if (has[i] == 1) flag = 1;
}
memset(m, 63, sizeof(m));
for (int i = 1; i <= N; ++ i) m[i][i] = 0;
for (int i = 1; i <= M; ++ i) {
read(a), read(b), read(c);
//处理重边
m[a][b] = min(m[a][b], c);
m[b][a] = m[a][b];
}
//用Floyd处理出两点之间能达到的最大阙值
fr(k, 1, N) fr(i, 1, N) {
if (i == k) continue;
fr(j, 1, N) {
if (i == j || j == k) continue;
if (m[i][j] != INF)
m[i][j] = max(m[i][j], min(m[i][k], m[k][j]));
else m[i][j] = min(m[i][k], m[k][j]);
}
}
fr(i, 1, (1 << K) - 1) fr(j, 1, K)
if (i & (1 << j - 1)) {
fr(k, 1, K) if (!(i & (1 << k - 1))) {
if (m[has[j]][has[k]] < dp[i][j]) continue;
dp[i | (1 << k - 1)][k] = max(dp[i | (1 << k - 1)][k], dp[i][j] + 1);
}
//如果从该点能回到起点,更新答案
if (m[has[j]][1] >= dp[i][j]) ans = max(ans, dp[i][j]);
}
printf("%d\n", ans + flag);
return 0;
} [codevs] P1358 棋盘游戏
时间限制: 1 s
空间限制: 64000 KB
题目等级 : 大师 Master
题目描述 Description
这个游戏在一个有10*10个格子的棋盘上进行,初始时棋子位于左上角,终点为右下角,棋盘上每个格子内有一个0到9的数字,每次棋子可以往右方或下方的相邻格子移动,求一条经过数字之和最小且经过0到9的所有数字的合法路径,输出其长度。(经过的数字包括左上角和右下角)
输入输出描述
输入描述 Input Description
输入包含10行,每行10个数字,以空格隔开,表示棋盘格子上的权值。数据保证存在合法路径。
输出描述 Output Description
输出所求路径的权值和。
样例输入输出
样例输入 Sample Input
0 1 2 3 4 5 6 7 8 9
1 1 1 1 1 1 1 1 1 0
2 1 1 1 1 1 1 1 1 0
3 1 1 1 1 1 1 1 1 0
4 1 1 1 1 1 1 1 1 0
5 1 1 1 1 1 1 1 1 0
6 1 1 1 1 1 1 1 1 0
7 1 1 1 1 1 1 1 1 0
8 1 1 1 1 1 1 1 1 0
9 1 1 1 1 1 1 1 1 5
样例输出 Sample Output
50
数据范围及提示 Data Size & Hint
【样例解释】
先一直向右走到第一行末尾,再竖直向下走位最优路径。
比较简单的状压DP。事实上BFS也可以过(我们假设它过不了)。矩形DP和状压DP的结合。思路很简单,\(dp[i][j][k]\)表示前i行j列状态为k的最小数字和。状态转移方程太好写了= =\(dp[i][j][k]=Min(dp[i][j][k|(1<<m[i][j])], dp[i-1][j][k]+m[i][j], dp[i][j-1][k]+m[i][j])\)
/*
作者:曼珠沙华
题目:p1358 棋盘游戏
*/
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 12;
int m[MAXN][MAXN];
//dp[i][j][k]表示前i行j列状态为k的最小数字和
int dp[MAXN][MAXN][1 << MAXN];
template <typename _Tp>
inline _Tp read(_Tp &x) {
char ch = getchar( ); bool f = 0; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
if (f) x = -x; return x;
}
int main( ) {
memset(dp, 63, sizeof(dp));
for (int i = 1; i <= 10; ++ i)
for (int j = 1; j <= 10; ++ j) read(m[i][j]);
dp[1][1][1 << m[1][1]] = m[1][1];
for (int i = 1; i <= 10; ++ i)
for (int j = 1; j <= 10; ++ j)
for (int k = 0; k < (1 << 10); ++ k) {
if (i != 1) dp[i][j][k | (1 << m[i][j])] =
min(dp[i][j][k | (1 << m[i][j])], dp[i - 1][j][k] + m[i][j]);
if (j != 1) dp[i][j][k | (1 << m[i][j])] =
min(dp[i][j][k | (1 << m[i][j])], dp[i][j - 1][k] + m[i][j]);
}
printf("%d\n", dp[10][10][(1 << 10) - 1]);
return 0;
}P1441 砝码称重
题目描述
现有n个砝码,重量分别为a1,a2,a3,……,an,在去掉m个砝码后,问最多能称量出多少不同的重量(不包括0)。
输入输出格式
输入格式:
输入文件weight.in的第1行为有两个整数n和m,用空格分隔
第2行有n个正整数a1,a2,a3,……,an,表示每个砝码的重量。
输出格式:
输出文件weight.out仅包括1个整数,为最多能称量出的重量。
输入输出样例
输入样例#1:
3 1
1 2 2输出样例#1:
3说明
【样例说明】
在去掉一个重量为2的砝码后,能称量出1,2,3共3种重量。
【数据规模】
对于20%的数据,m=0;
对于50%的数据,m≤1;
对于50%的数据,n≤10;
对于100%的数据,n≤20,m≤4,m<n,ai≤100。
用状压的直观思路就是枚举每一种合法的去掉m个砝码后的情况。假设现在有一个集合\(b[i]\)表示重量为i可以被称出。那么枚举状态的哪一位是1,如果是当前第j位是1,那么之前称过的所有重量都可以在原来的基础上再加上\(w[j]\),也就是\(b<<w[j]\),那么\(b=b|b<<w[j]\)。最后统计b中有多少个元素即可。这个b可以用bitset维护。
#include<bitset>
#include<cstdio>
#include<iostream>
#define f(i,x,n) for(int i=x;i<=n;++i)
using namespace std;
int n, m, a[21];
int ans;
int bit(int x) {
int cnt = 0;
f(i, 0, n - 1) if (x & (1 << i)) cnt++;
return cnt;
}
int main() {
cin >> n >> m;
f(i, 0, n - 1) cin >> a[i];
f(i, 0, (1<<n)-1) if (bit(i) == n - m) {
bitset<2010> t;
t[0] = 1;
f(j, 0, n - 1) if (i & (1<<j)) {
t = t | t << a[j];
ans = max(ans, (int)t.count());
}
}
cout << ans - 1 << endl;
return 0;
}P2622 关灯问题II
题目描述
现有n盏灯,以及m个按钮。每个按钮可以同时控制这n盏灯——按下了第i个按钮,对于所有的灯都有一个效果。按下i按钮对于第j盏灯,是下面3中效果之一:如果a[i][j]为1,那么当这盏灯开了的时候,把它关上,否则不管;如果为-1的话,如果这盏灯是关的,那么把它打开,否则也不管;如果是0,无论这灯是否开,都不管。
现在这些灯都是开的,给出所有开关对所有灯的控制效果,求问最少要按几下按钮才能全部关掉。
输入输出格式
输入格式:
前两行两个数,n m
接下来m行,每行n个数,a[i][j]表示第i个开关对第j个灯的效果。
输出格式:
一个整数,表示最少按按钮次数。如果没有任何办法使其全部关闭,输出-1
输入输出样例
输入样例#1:
3
2
1 0 1
-1 1 0输出样例#1:
2说明
对于20%数据,输出无解可以得分。
对于20%数据,n<=5
对于20%数据,m<=20
上面的数据点可能会重叠。
对于100%数据 n<=10,m<=100
我们当然是输出无解啦其实这题比较简单。根据题目定义,\(a[i]=0\)不管,那我们就不管了,当\(a[i]=1\)或\(a[i]=-1\)时,这是什么操作?显然是取反操作。\(f[i]\)表示状态为i的最少按钮数。转移真的很简单,看代码。
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
const int INF = 0x3f3f3f3f;
int n, m, a[110][1100];
int f[1100];
int main() {
cin >> n >> m;
for (int i = 1; i <= m; ++ i)
for (int j = 1; j <= n; ++ j)
cin >> a[i][j];
for (int i = 0; i < (1 << n); ++ i) f[i] = INF;
f[0] = 0;
for (int i = 0; i < (1 << n); ++ i)
for (int j = 1; j <= m; ++ j) {
int t = i;
for (int k = 0; k < n; ++ k)
if (((a[j][k + 1] == 1) && !(i & 1 << k)) ||
(a[j][k + 1] == -1) && (i & 1 << k))
t ^= 1 << k;
f[t] = min(f[t], f[i] + 1);
}
if (f[(1 << n) - 1] == INF) cout << "-1" << endl;
else cout << f[(1 << n) - 1] << endl;
return 0;
}
[HDU] P3001 Travelling
限制:6000/3000毫秒(Java /其他)内存限制:32768/32768 K
(Java /其他)总提交(7907):接受的提交(s):2590
问题描述
在coding了这么多天之后,Acmer先生想要好好休息一下,旅行当然是最好的选择!他已决定访问N个城市,而Acmer先生坚持要访问所有的N个城市!他也不介意哪个城市是他的起点,因为会有超人可以把他带到任何城市,但只有一次召唤超人的机会。当然,这里有m条道路会照常收费。不过Acmer先生太无聊了,他不想参观同一城市两次以上(不含两次)!并且在此前提下,他想把总费用降到最低!他很懒惰,所以他找到了你,向你寻求帮助。
输入
有多组测试数据,第一行是两个整数n(1<n=10)和m,这意味着他需要访问N个城市,可以选择M条道路,然后接下来m行,每行三个整数a、b和c(1<a,b <=n),意思是a和b之间有一条路费用是C。
输出
输出他应该支付的最低费用,如果找不到这样的路线,输出-1。
有意思。简化一下题意,就是给你一张无向图(可能有重边),你可以从任意一节点出发,在不经过同一城市两次的前提下,经过所有的城市。某两节点间有有权边,问是否有解,如果有,最小费用是多少。可以看出本题事实上是TSP问题的变形,考虑每个节点最多只能经过两次,也就是有0,1,2三种情况,所以要用鬼畜的三进制状压。我们先用一个\(p3[]\)数组表示3的多少次幂,\(p3[0] = 1\),直接递推。正常的状压最重要的是状态的压缩,那么如何将状态压缩成三进制呢?在二进制状压时,我们是用数在二进制表示下的每一位表示该对应元素的状态,那么我们显然可以用一个数组模拟这个表达方式,设\(tri[i][j]\)表示状态为\(i\)(\(i\)为三进制数)的第\(j\)位上的经过次数(不写成try是因为和C++关键字冲突)。在更新时,根据题意,一共要满足两个条件:1.要经过所有城市(即\(tri[i][1…n]\)均不能为0);2.每个城市不能经过两次(即\(tri[i][1…n]<=2\)),然后正常套路。
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXX = 60010;
const int MAXN = 12;
int n, w, m[MAXN][MAXN];
int p3[MAXN], tri[MAXX][MAXN], ans, dp[MAXX][MAXN];
//flag判断当前状态能否更新ans,flag2判断是否有解
bool flag, flag2;
template <typename _Tp>
inline _Tp read(_Tp &x) {
char ch = getchar( ); bool f = 0; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
if (f) x = -x; return x;
}
int main( ) {
p3[0] = 1;
for (int i = 1; i <= MAXN; ++ i) p3[i] = p3[i - 1] * 3;
//三进制数的转化
for (int i = 1, tmp = i; i <= MAXX; ++ i, tmp = i)
for (int j = 1; j <= MAXX; ++ j) {
tri[i][j] = tmp % 3;
tmp /= 3;
if (!tmp) break;
}
while (scanf("%d%d", &n, &w) == 2) {
ans = INF; flag2 = false;
memset(m, 63, sizeof(m));
int x, y, z;
//处理重边
for (int i = 1; i <= w; ++ i) {
read(x), read(y), read(z);
m[x][y] = min(m[x][y], z);
m[y][x] = m[x][y];
}
memset(dp, 63, sizeof(dp));
//任意一点均可作为起点且花费为0
for (int i = 1; i <= n; ++ i) dp[p3[i - 1]][i] = 0;
for (int i = 1; i < p3[n]; ++ i) {
flag = true;
for (int j = 1; j <= n; ++ j) {
//如果有某一位是0,说明有城市不能到达,不满足条件,不更新答案
if (!tri[i][j]) flag = false;
for (int k = 1; k <= n; ++ k) if (k != j && tri[i][k] < 2)
dp[i + p3[k - 1]][k] = min(dp[i + p3[k - 1]][k], dp[i][j] + m[j][k]);
}
if (flag) for (int j = 1; j <= n; ++ j)
if (ans > dp[i][j]) ans = dp[i][j], flag2 = true;
}
if (!flag2) printf("-1\n");
else printf("%d\n", ans);
}
return 0;
}P1896 [SCOI2005]互不侵犯
题目描述
在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子。
注:数据有加强(2018/4/25)
输入输出格式
输入格式:
只有一行,包含两个数N,K ( 1 <=N <=9, 0 <= K <= N * N)
输出格式:
所得的方案数
输入输出样例
输入样例#1:
3 2输出样例#1:
16首先这道题并不是线性的了,而是矩形,却又不是矩形DP。每个国王可以影响到一个3*3的范围,这样也比较难搞。考虑到每一行都是相似的,我们不妨将矩形分成若干行来做。
显然对于每一行,我们可以\(O(2^nn)\)预处理出所有可行的状态,每一行都必然是这些状态中的其中一种。设\(dp[i][j][k]\)表示前i行,第i行状态为j,放了k个国王的方案总数。然后对于每一行,枚举可能状态,枚举放置的国王总数,再来一层枚举上一行的状态判断合法(好暴力),因为当前行合法与否可以看成只与前一行状态有关(感性理解),所以这样显然是对的。
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define f(i, x, n) for(int i=x;i<=n;++i)
using namespace std;
typedef long long LL;
const int MAXX = 110;
int N, K;
int tot, s0, s[MAXX], num[MAXX];
LL ans, dp[10][MAXX][MAXX];
int main() {
cin >> N >> K;
f(i, 0, (1 << N) - 1) {
if (i & (i << 1)) continue;
tot = 0;
f(j, 0, N - 1)
if (i & (1 << j)) tot++; //统计放置数量
s[++ s0] = i; //标记可行方案
num[s0] = tot;
}
dp[0][1][0] = 1;
f(i, 1, N) f(j, 1, s0) f(k, 0, K)
if (k >= num[j]) f(t, 1, s0)
if (!(s[t] & s[j]) && !(s[t] & (s[j] << 1)) && !(s[t] & s[j] >> 1))
dp[i][j][k] += dp[i - 1][t][k - num[j]];
f(i, 1, s0) ans += dp[N][i][K];
cout << ans << endl;
return 0;
}你要先大法师再打表我也不会拦你的。
#include<cstdio>
#include<iostream>
long long a[300]={
1,
4,0,0,0,
9,16,8,1,0,0,0,0,0,
16,78,140,79,0,0,0,0,0,0,0,0,0,0,0,0,
25,228,964,1987,1974,978,242,27,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
36,520,3920,16834,42368,62266,51504,21792,3600,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
49,1020,11860,85275,397014,1220298,2484382,3324193,2882737,1601292,569818,129657,18389,1520,64,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
64,1806,29708,317471,2326320,12033330,44601420,119138166,229095676,314949564,305560392,204883338,91802548,25952226,4142000,281571,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
81,2968,65240,962089,10087628,77784658,450193818,1979541332,6655170642,17143061738,33787564116,50734210126,57647295377,49138545860,31122500764,14518795348,4959383037,1237072414,224463798,29275410,2673322,163088,6150,125,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
},b,c;
int main(){
scanf("%d%d",&b,&c);
std::cout<<a[(b-1)*b*(2*b-1)/6+c-1];
}P2704 [NOI2001]炮兵阵地
题目描述
司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
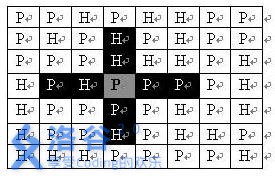
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入输出格式
输入格式:
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符(‘P’或者‘H’),中间没有空格。按顺序表示地图中每一行的数据。N≤100;M≤10。
输出格式:
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
输入输出样例
输入样例#1:
5 4
PHPP
PPHH
PPPP
PHPP
PHHP输出样例#1:
6这个影响范围比互不侵犯更鬼畜。十字???不会下一个
这样每一行不仅要受到前一行的影响,还要受到前一行的前一行的影响,这咋办?
这题范围不大,我们不妨鬼畜暴力一点,他不是受两行影响吗?我把他转化成只受前一行影响就行了。如何转化?反正都状压了,也没人说不能一次压两行啊?
设\(dp[i][j][k]\)表示当前状态是i,上一行状态是j,当前考虑到了第k行。
先处理出第一行,然后依次递推,各种神奇玄学的判断,然后你会发现
这题就没了 MLE了。
让dp的最后一维滚 将dp的最后一维滚动优化成[3]。然后就真没了。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define f(i, x, n) for(int i=x;i<n;++i)
using namespace std;
const int MAXN = 100;
const int MAXM = 10;
int N, M, ans;
int t[MAXN], sum[(1<<10)], dp[(1<<10)][(1<<10)][3];
void init() {
cin >> N >> M;
f(i, 0, N) f(j, 0, M) {
char x; cin >> x;
t[i] <<= 1, t[i] += (x == 'H' ? 1 : 0);
}
}
int getsum(int i) {
int tot = 0;
while(i) { if (i & 1) ++ tot; i >>= 1; }
return tot;
}
aA
bool pd(int s) { return ((s & (s << 1)) || (s & (s << 2))); }
int main() {
init();
f(i, 0, (1 << M)) sum[i] = getsum(i);
f(l, 0, (1 << M)) f(s, 0, (1 << M))
if (!(l & s || l & t[0] || s & t[1] || pd(l) || pd(s)))
dp[l][s][1] = sum[s] + sum[l];
f(i, 2, N) f(l, 0, (1 << M)) {
if (l & t[i - 1] || pd(l)) continue;
f(s, 0, (1 << M)) {
if (s & t[i] || l & s || pd(s)) continue;
f(p, 0, (1 << M)) {
if (p & l || p & s || p & t[i - 2] || pd(p)) continue;
dp[l][s][i % 3] = max(dp[l][s][i % 3],
dp[p][l][(i - 1) % 3] + sum[s]);
}
}
}
f(l, 0, (1 << M)) f(s, 0, (1 << M))
ans = max(ans, dp[l][s][(N - 1) % 3]);
cout << ans << endl;
return 0;
}