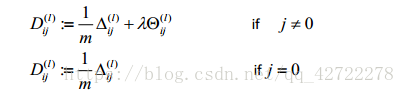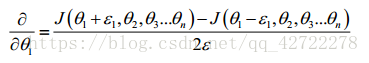吴恩达教授的机器学习课程的第五周相关内容：

1、代价函数

首先引入一些便于稍后讨论的新标记方法：
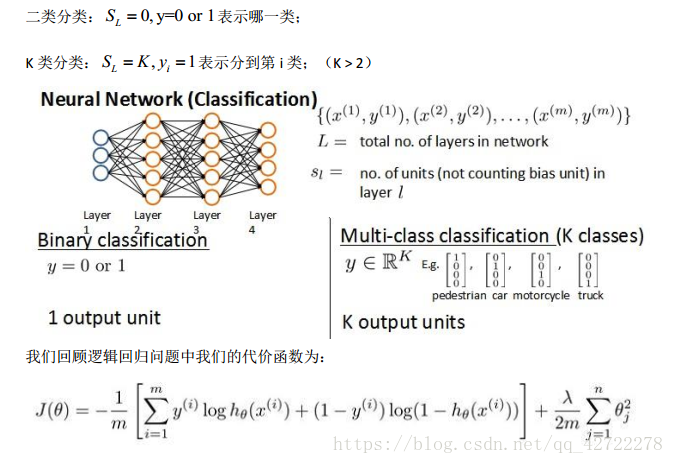
假设神经网络的训练样本有 m 个，每个包含一组输入 x 和一组输出信号 y， L 表示神经网络层数， S I 表示每层的 neuron 个数(SL 表示输出层神经元个数)， S L 代表最后一层中处理
单元的个数。
将神经网络的分类定义为两种情况：二类分类和多类分类，
在这里插入图片描述
在逻辑回归中，我们只有一个输出变量，又称标量（scalar），也只有一个因变量 y，但是在神经网络中，我们可以有很多输出变量，我们的 h 是一个维度为 K 的向量，并且我们训练集中的因变量也是同样维度的一个向量，因此我们的代价函数会比逻辑回归更加复杂一些，为：在这里插入图片描述
小结：代价函数的输出更复杂一些，但本质和之前的输出是一样的。

2、反向传播算法

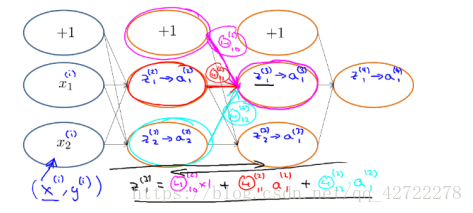
之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法，我们从第一层开始正向一层一层进行计算，直到最后一层的 h。
现在，为了计算代价函数的偏导数
，我们需要采用一种反向传播算法，也就是首先计算最后一层的误差，然后再一层一层反向求出各层的误差，直到倒数第二层。
以一个例子来说明反向传播算法。
假设我们的训练集只有一个实例，我们的神经网络是一个四层的神经网络，
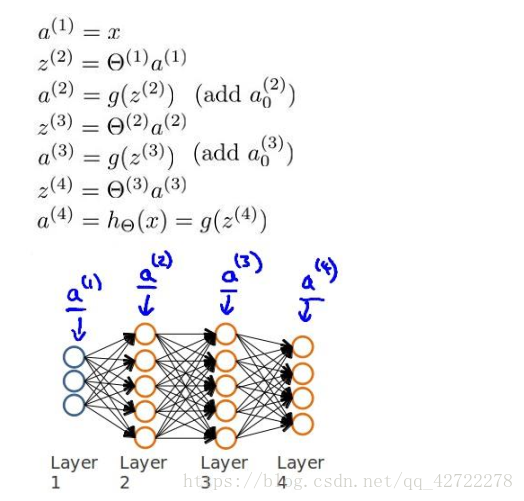
其中 K =4， $S_{L}=4$ ,L=4：前向传播算法：
在这里插入图片描述

计算代价函数的偏导数:
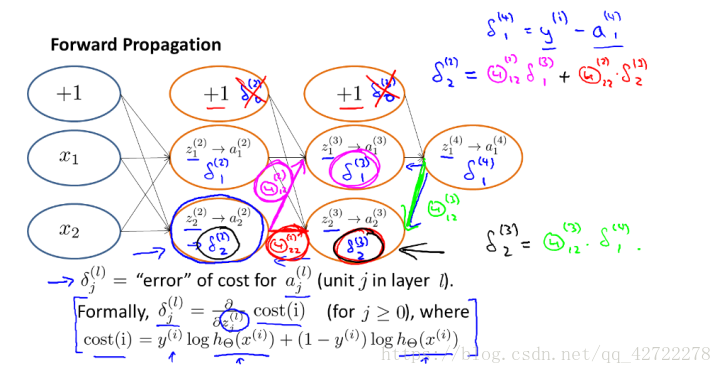
在这里插入图片描述
前向传播算法：

反向传播算法做的是：

小结：反向传播，顾名思义是从后往前推导的可以结合着前向传播理解。

3、实现注意：展开参数

在这里插入图片描述
小结：这里是为了更好的使用 $\theta$ 而用的。

4、梯度检验

当我们对一个较为复杂的模型（例如神经网络）使用梯度下降算法时，可能会存在一些不容易察觉的错误，意味着，虽然代价看上去在不断减小，但最终的结果可能并不是最优解。
为了避免这样的问题，我们采取一种叫做梯度的数值检验（Numerical Gradient Checking）方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。
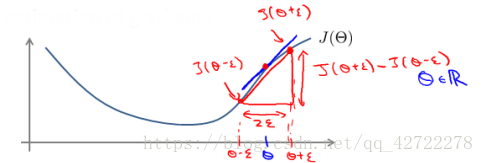
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。
在这里插入图片描述
当 $\theta$ 是一个向量时，我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对
一个参数的改变进行检验，下面是一个只针对 $\theta_{1}$ 进行检验的示例：

小结：估计梯度值来检验我们计算的导数值是否真的是我们要求的。

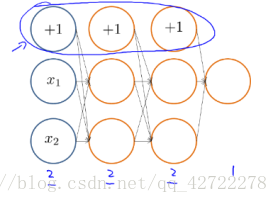
5、随机初始化

任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为 0，这样的初始方法对于逻辑回归来说是可行的，但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为 0，这将意味着我们第二层的所有激活单元都会有相同的值。同理，如果我们初始所有的参数都为一个非 0 的数，结果也是一样的。
小结：避免激活单元有相同的值。

6、综合起来

小结一下使用神经网络时的步骤：
网络结构：第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多少个单元。
第一层的单元数即我们训练集的特征数量。
最后一层的单元数是我们训练集的结果的类的数量。
如果隐藏层数大于 1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好。
我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络：

参数的随机初始化
利用正向传播方法计算所有的 hθ(x)
编写计算代价函数 J 的代码
利用反向传播方法计算所有偏导数
利用数值检验方法检验这些偏导数
使用优化算法来最小化代价函数
小结：训练神经网络的步骤。

7、第五周编程题

1、nnCostFunction.m
h = eye(num_labels);
y = h(y,:); %5000x10
a1 = [ones(m, 1) X]; %5000x401
z2 = a1 * Theta1’ ;
a2 = sigmoid(z2);
n = size(a2,1);
a2 = [ones(n, 1) a2] ; %5000x26
a3 = sigmoid(a2 * Theta2’); %5000x10
J = sum( sum( -y.* log(a3) - (1-y).log(1-a3) ))/ m;
% pay attention :" Theta1(:,2:end) " , no “Theta1” .
regularized = lambda/(2m) * (sum(sum(Theta1(:,2:end).^2)) + sum(sum(Theta2(:,2:end).^2)) );
J = J + regularized;

%part2

delta3 = a3 - y; %500010
delta2 = delta3 * Theta2; %500026
delta2 = delta2(:, 2 : end);
delta2 = delta2 .* sigmoidGradient(z2); %5000*25

Delta_1 = zeros(size(Theta1));
Delta_2 = zeros(size(Theta2));

扫描二维码关注公众号，回复： 3661258 查看本文章

Delta_1 = Delta_1 + delta2’ * a1;
Delta_2 = Delta_2 + delta3’ * a2;

Theta1_grad = ((1 / m) * Delta_1) + ((lambda / m) * Theta1);
Theta2_grad = ((1 / m) * Delta_2) + ((lambda / m) * Theta2);

Theta1_grad(:, 1) = Theta1_grad(:, 1) - ((lambda / m) * (Theta1(:, 1)));
Theta2_grad(:, 1) = Theta2_grad(:, 1) - ((lambda / m) * (Theta2(:, 1)));

这周的关于公式怎么推导怎么来的是一头雾水，日后看看李航老师的《统计学习方法吧》
2、sigmoidGradient.m
g=sigmoid(z).*(1-sigmoid(z))

机器学习之旅（五）