机器学习（五）：线性模型

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/eeeee123456/article/details/80095171

引言：
    线性模型（linear modal）试图学得一个通过属性的线性组合来进行预测的函数。本文介绍两种经典的线性模型，分别是回归任务中的线性回归（linear regression）与二分类任务中的逻辑回归（logistic regression）。
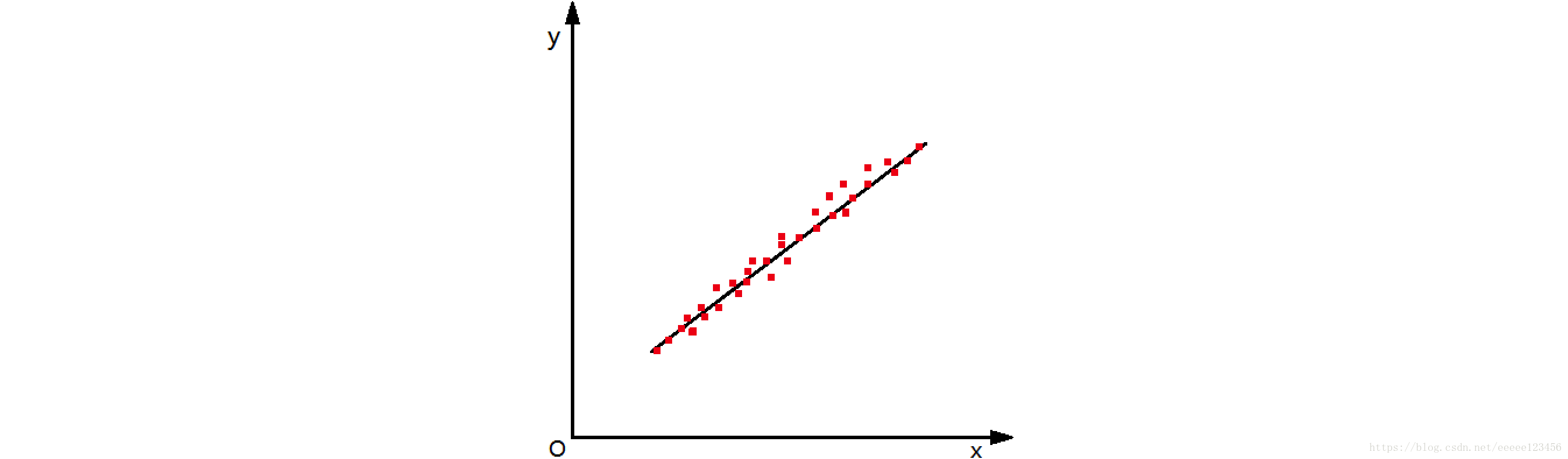
    如图1，在二维空间中有一些样本点，我们用一条直线对这些点进行拟合，该直线称为最佳拟合直线。线性回归就是根据训练集，寻找对训练样本的最佳拟合直线；逻辑回归则是利用“单位跳跃函数”将线性模型产生的预测值转换为0/1值，从而实现二分类任务。

图1

一、数学预备知识

1.方向导数

如果函数$f(x,y)$在点$P_0(x_0,y_0)$可微分，那么函数在该点沿任一方向$l$的方向导数存在，且有

$$\left.\frac{∂f}{∂l} \right| _{(x_0,y_0)}=f_x(x_0,y_0)\cosα+f_y(x_0,y_0)\cosβ$$ 其中 $\cosα$， $\cosβ$是方向 $l$的方向余弦。
（α为 $l$与x轴正向夹角，β为 $l$与y轴正向夹角。方向导数反映的是函数沿任一指定方向的变化率问题）
例1
求函数$z=xe^{2y}$在点$P(1,0)$处沿从点$P(1,0)$到点$Q(2,-1)$的方向的方向导数
解：
这里方向$l$即向量$\vec {PQ}=(1,-1)$的方向，与$l$同向的单位向量为$e_l=({1\over\sqrt{2}},{1\over\sqrt{2}})$。
因为函数可微分，且 $$Z_x(1,0)=e^{2y}=1$$ $$Z_y(1,0)=2xe^{2y}=2$$ 故所求方向导数为 $$\left.\frac{∂Z}{∂l} \right| _{(1,0)}=1\times{1\over\sqrt{2}}+2\times(-{1\over\sqrt{2}})=-{\sqrt{2}\over2}$$

2.梯度

与方向导数有关联的一个概念是函数的梯度。在二元函数的情形，设函数$f(x,y)$在平面区域D内具有一阶连续偏导数，则对于每一点$P_0(x_0,y_0)∈D$，都可定出一个向量

$$f_x(x_0,y_0){\bf i}+f_y(x_0,y_0)\bf j$$ 这向量称为函数 $f(x,y)$在点 $P_0(x_0,y_0)$的梯度，记作 ${\bf grad}\ f(x_0,y_0)$或 $∇f(x_0,y_0)$，即 $${\bf grad}\ f(x_0,y_0)=∇f(x_0,y_0)=f_x(x_0,y_0){\bf i}+f_y(x_0,y_0)\bf j$$ 其中 $∇={∂\over{∂x}}{\bf i}+{∂\over{∂y}}{\bf j}$称为（二维的）向量微分算子或Nabla算子， $∇f={{∂f}\over{∂x}}{\bf i}+{{∂f}\over{∂y}}{\bf j}$。
如果函数 $f(x,y)$在点 $P_0(x_0,y_0)$可微分， $e_l=(\cosα,\cosβ)$是与方向 $l$同向的单位向量，则 $$\left.\frac{∂f}{∂l} \right| _{(x_0,y_0)}=f_x(x_0,y_0)\cosα+f_y(x_0,y_0)\cosβ={\bf grad}\ f(x_0,y_0)\cdot e_l=|{\bf grad}\ f(x_0,y_0)|\cosθ$$ 其中 $θ=<{\bf grad}\ f(x_0,y_0),e_l>$。
这一关系式表明了函数在一点的梯度与函数在这点的方向导数间的关系。特别的：
① $θ=0$，即方向 $e_l$与梯度 ${\bf grad}\ f(x_0,y_0)$的方向相同时，函数 $f(x,y)$增加最快。此时，函数在这个方向的方向导数达到最大值，这个最大值就是梯度 ${\bf grad}\ f(x_0,y_0)$的模，即 $$\left.\frac{∂f}{∂l} \right| _{(x_0,y_0)}=|{\bf grad}\ f(x_0,y_0)|$$ ② $θ=π$，即方向 $e_l$与梯度 ${\bf grad}\ f(x_0,y_0)$的方向相反时，函数f $(x,y)$减少最快，函数在这个方向的方向导数达到最小值，即 $$\left.\frac{∂f}{∂l} \right| _{(x_0,y_0)}=-|{\bf grad}\ f(x_0,y_0)|$$ ③ $θ={π\over 2}$，即方向 $e_l$与梯度 ${\bf grad}\ f(x_0,y_0)$的方向正交时，函数的变化率为零，即 $$\left.\frac{∂f}{∂l} \right| _{(x_0,y_0)}=|{\bf grad}\ f(x_0,y_0)|\cosθ=0$$ 例2
设$f(x,y)={1\over 2}(x^2+y^2)$，$P_0(1,1)$，求
①$f(x,y)$在$P_0$处增加最快的方向以及$f(x,y)$沿这个方向的方向导数；
②$f(x,y)$在$P_0$处减少最快的方向以及$f(x,y)$沿这个方向的方向导数；
③$f(x,y)$在$P_0$处的变化率为零的方向；
解：
①$f(x,y)$在$P_0$处沿$∇f(1,1)$的方向增加最快 $$∇f(1,1)=(x{\bf i}+y{\bf j})|_{(1,1)}={\bf i}+{\bf j}$$ 故所求方向可取为 $$n={{∇f(1,1)}\over{|∇f(1,1)|}}={1\over{\sqrt 2}}{\bf i}+{1\over{\sqrt 2}}{\bf j}$$ 方向导数为 $$\left.\frac{∂f}{∂n} \right| _{(1,1)}=|∇f(1,1)|=\sqrt 2$$ ②$f(x,y)$在$P_0$处沿$-∇f(1,1)$的方向减少最快，这个方向可取为 $$n_1=-n=-{1\over{\sqrt 2}}{\bf i}-{1\over{\sqrt 2}}{\bf j}$$ 方向导数为 $$\left.\frac{∂f}{∂n_1} \right| _{(1,1)}=-|∇f(1,1)|=-\sqrt 2$$ ③$f(x,y)$在$P_0$处沿垂直于$∇f(1,1)$的方向变化率为零，这个方向是 $$n_2=-{1\over{\sqrt 2}}{\bf i}+{1\over{\sqrt 2}}{\bf j}$$ 或 $$n_3={1\over{\sqrt 2}}{\bf i}-{1\over{\sqrt 2}}{\bf j}$$

3.带佩亚诺余项的泰勒公式

若$f(x)$在$x=a$有$n$阶微商，即$f^{(n)}(a)$存在，则当$x\rightarrow a$时有

$$f(x)=f(a)+f'(a)(x-a)+{{f''(a)}\over{2!}}(x-a)^2+\cdots+{{f^{(n)}(a)}\over{n!}}(x-a)^n+\rm o((x-a)^n)$$ 其中多项式 $$f(a)+f'(a)(x-a)+\cdots+{{f^{(n)}(a)}\over{n!}}(x-a)^n$$ 称为 $f(x)$在 $a$点的 $n$阶泰勒多项式。

4.二元函数的泰勒公式

设$f(x,y)$在$P_0(x_0,y_0)$的某领域$\rm O(P_0)$内有直到$n+1$阶连续偏导数，则对$\rm O(P_0)$内任一点$(x_0+Δx ,y_0+Δy)$，存在$θ∈(0,1)$，使得

$$f(x_0+Δx ,y_0+Δy)=\sum_{k=0}^n{1\over{k!}}\left(\frac{∂}{∂x}Δx+\frac{∂}{∂y}Δy\right)^kf(x_0,y_0)+R_n$$ 其中 $$R_n={1\over{(n+1)!}}\left(\frac{∂}{∂x}Δx+\frac{∂}{∂y}Δy\right)^{n+1}f(x_0+θΔx ,y_0+θΔy)$$ 当 $n=1$，忽略余项 $R_n$，即得函数的一阶泰勒展开式 $$f(x_0+Δx ,y_0+Δy)≈f(x_0,y_0)+{f'}_x(x_0,y_0)Δx+{f'}_y(x_0,y_0)Δy$$ 利用泰勒公式，可以用 $n$阶多项式逼近函数 $f(x,y)$， $n$越大则误差越小，近似程度越好。

二、线性回归

1.最小二乘法

    给定训练集$D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$，其中$x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T$，$x_i^{(j)}$是第$i$个实例的第$j$个特征。线性回归试图学得

$$f(x_i)=w^Tx_i+b，使得f(x_i)≈y_i$$ 其中 $w=(w_1,w_2,...,w_n)^T$。
    如何确定 $w$和 $b$呢？一个常用的方法是极小化其平方损失函数，即使均方误差最小化，得 $$(w^*,b^*)=arg\min_{(w,b)}\sum_{i=1}^N(f(x_i)-y_i)^2=arg\min_{(w,b)}\sum_{i=1}^N(y_i-w^Tx_i-b)^2$$     基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。均方误差有非常好的几何意义，它对应了欧几里得距离，在线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上的欧几里得距离之和最小。

2.求解$w$和$b$

    为了讨论方便，我们把$w$和$b$吸收入向量形式$\hat w=(w^T;b)^T$。把训练集$D$表示为一个$N\times (n+1)$大小的矩阵$X$，其中每行对应于一个实例$x_i$，该行前$n$个元素对应于$x_i$的$n$个属性，最后一个元素恒置为1。即

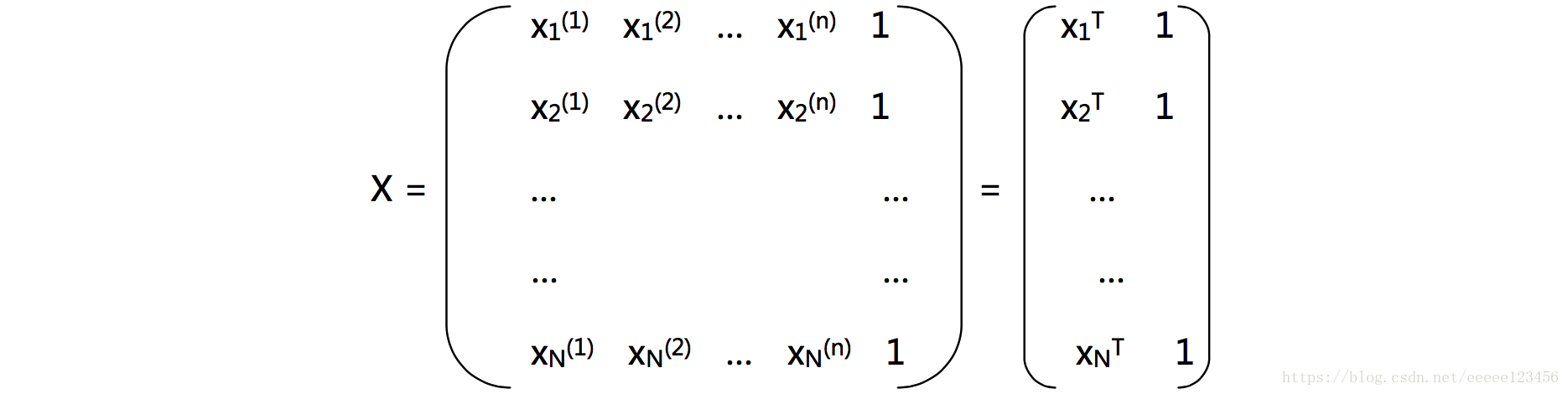
再把类别也写成向量形式$y=(y_1,y_2,\cdots,y_N)^T$，则有

$${\hat w}^*=arg\min_{\hat w}(y-X\hat w)^T(y-X\hat w)$$ 令 $E=(y-X\hat w)^T(y-X\hat w)$，对 $\hat w$求导得到 $$E_{\hat w}=2X^T(X{\hat w}-y)$$ 令上式为零可求得 $\hat w$的最优解。当 $X^TX$为满秩矩阵时，可解得 $$\hat w=(X^TX)^{-1}X^Ty\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$$ 从而求解出 $w$和 $b$，得到线性回归模型： $$y=w^Tx+b$$

3.岭回归（ridge regression）

    然而，现实任务中$X^TX$往往不是满秩矩阵，无法计算$(X^TX)^{-1}$。为了解决这个问题，统计学家引入岭回归。简单说来，岭回归就是在矩阵$X^TX$上加入一个$λI$，使得能对$X^TX+λI$求逆。其中$I$是$N\times N$的单位矩阵。则

$$\hat w=(X^TX+λI)^{-1}X^Ty$$     这里通过引入 $λ$来限制所有 $w$之和，通过引入该惩罚项，能够减少不重要的参数，这个技术在统计学中也叫做缩减（shrinkage）。可以通过交叉验证法，选取不同的 $λ$进行测试，最终得到一个使预测误差最小化的λ。

4.代码实现（python）

以下代码来自Peter Harrington《Machine Learing in Action》。
代码如下（保存为regression.py）：

# -- coding: utf-8 --
from numpy import *

def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([float(lineArr[0]), 1.0]) # dataMat为吸收后的X，即将特征值最后一个元素恒置为1
        labelMat.append(float(lineArr[1]))       # labelMat为对应的标记类别
    return dataMat,labelMat

def standRegres(xArr,yArr):
    # xArr为特征值，yArr为对应的标记类别，该函数用于计算w和b
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat               # 计算xTx
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T*yMat)      # 若xTx不为零，则根据式(1)计算w^
    return ws

数据集如下（保存为ex0.txt）：

0.067732    3.176513
0.427810    3.816464
0.995731    4.550095
0.738336    4.256571
0.981083    4.560815
0.526171    3.929515
0.378887    3.526170
0.033859    3.156393
0.132791    3.110301
0.138306    3.149813
0.247809    3.476346
0.648270    4.119688
0.731209    4.282233
0.236833    3.486582
0.969788    4.655492
0.607492    3.965162
0.358622    3.514900
0.147846    3.125947
0.637820    4.094115
0.230372    3.476039
0.070237    3.210610
0.067154    3.190612
0.925577    4.631504
0.717733    4.295890
0.015371    3.085028
0.335070    3.448080
0.040486    3.167440
0.212575    3.364266
0.617218    3.993482
0.541196    3.891471
0.045353    3.143259
0.126762    3.114204
0.556486    3.851484
0.901144    4.621899
0.958476    4.580768
0.274561    3.620992
0.394396    3.580501
0.872480    4.618706
0.409932    3.676867
0.908969    4.641845
0.166819    3.175939
0.665016    4.264980
0.263727    3.558448
0.231214    3.436632
0.552928    3.831052
0.047744    3.182853
0.365746    3.498906
0.495002    3.946833
0.493466    3.900583
0.792101    4.238522
0.769660    4.233080
0.251821    3.521557
0.181951    3.203344
0.808177    4.278105
0.334116    3.555705
0.338630    3.502661
0.452584    3.859776
0.694770    4.275956
0.590902    3.916191
0.307928    3.587961
0.148364    3.183004
0.702180    4.225236
0.721544    4.231083
0.666886    4.240544
0.124931    3.222372
0.618286    4.021445
0.381086    3.567479
0.385643    3.562580
0.777175    4.262059
0.116089    3.208813
0.115487    3.169825
0.663510    4.193949
0.254884    3.491678
0.993888    4.533306
0.295434    3.550108
0.952523    4.636427
0.307047    3.557078
0.277261    3.552874
0.279101    3.494159
0.175724    3.206828
0.156383    3.195266
0.733165    4.221292
0.848142    4.413372
0.771184    4.184347
0.429492    3.742878
0.162176    3.201878
0.917064    4.648964
0.315044    3.510117
0.201473    3.274434
0.297038    3.579622
0.336647    3.489244
0.666109    4.237386
0.583888    3.913749
0.085031    3.228990
0.687006    4.286286
0.949655    4.628614
0.189912    3.239536
0.844027    4.457997
0.333288    3.513384
0.427035    3.729674
0.466369    3.834274
0.550659    3.811155
0.278213    3.598316
0.918769    4.692514
0.886555    4.604859
0.569488    3.864912
0.066379    3.184236
0.335751    3.500796
0.426863    3.743365
0.395746    3.622905
0.694221    4.310796
0.272760    3.583357
0.503495    3.901852
0.067119    3.233521
0.038326    3.105266
0.599122    3.865544
0.947054    4.628625
0.671279    4.231213
0.434811    3.791149
0.509381    3.968271
0.749442    4.253910
0.058014    3.194710
0.482978    3.996503
0.466776    3.904358
0.357767    3.503976
0.949123    4.557545
0.417320    3.699876
0.920461    4.613614
0.156433    3.140401
0.656662    4.206717
0.616418    3.969524
0.853428    4.476096
0.133295    3.136528
0.693007    4.279071
0.178449    3.200603
0.199526    3.299012
0.073224    3.209873
0.286515    3.632942
0.182026    3.248361
0.621523    3.995783
0.344584    3.563262
0.398556    3.649712
0.480369    3.951845
0.153350    3.145031
0.171846    3.181577
0.867082    4.637087
0.223855    3.404964
0.528301    3.873188
0.890192    4.633648
0.106352    3.154768
0.917886    4.623637
0.014855    3.078132
0.567682    3.913596
0.068854    3.221817
0.603535    3.938071
0.532050    3.880822
0.651362    4.176436
0.901225    4.648161
0.204337    3.332312
0.696081    4.240614
0.963924    4.532224
0.981390    4.557105
0.987911    4.610072
0.990947    4.636569
0.736021    4.229813
0.253574    3.500860
0.674722    4.245514
0.939368    4.605182
0.235419    3.454340
0.110521    3.180775
0.218023    3.380820
0.869778    4.565020
0.196830    3.279973
0.958178    4.554241
0.972673    4.633520
0.745797    4.281037
0.445674    3.844426
0.470557    3.891601
0.549236    3.849728
0.335691    3.492215
0.884739    4.592374
0.918916    4.632025
0.441815    3.756750
0.116598    3.133555
0.359274    3.567919
0.814811    4.363382
0.387125    3.560165
0.982243    4.564305
0.780880    4.215055
0.652565    4.174999
0.870030    4.586640
0.604755    3.960008
0.255212    3.529963
0.730546    4.213412
0.493829    3.908685
0.257017    3.585821
0.833735    4.374394
0.070095    3.213817
0.527070    3.952681
0.116163    3.129283

运行命令如下：

最后求出的$ws$即$\hat w$。

三、逻辑回归

逻辑回归是一种分类模型，本文主要介绍二分类的逻辑回归。

1.Sigmoid函数

    给定训练集$D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$，其中$x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T$，$x_i^{(j)}$是第$i$个实例的第$j$个特征，$y_i∈{0,1}$为实例的类别。若用线性回归模型$y=w^Tx+b$对该训练集进行分类，分类图形如图2线A（此处设$x_i=(x_i^{(1)})^T$）所示：

图2
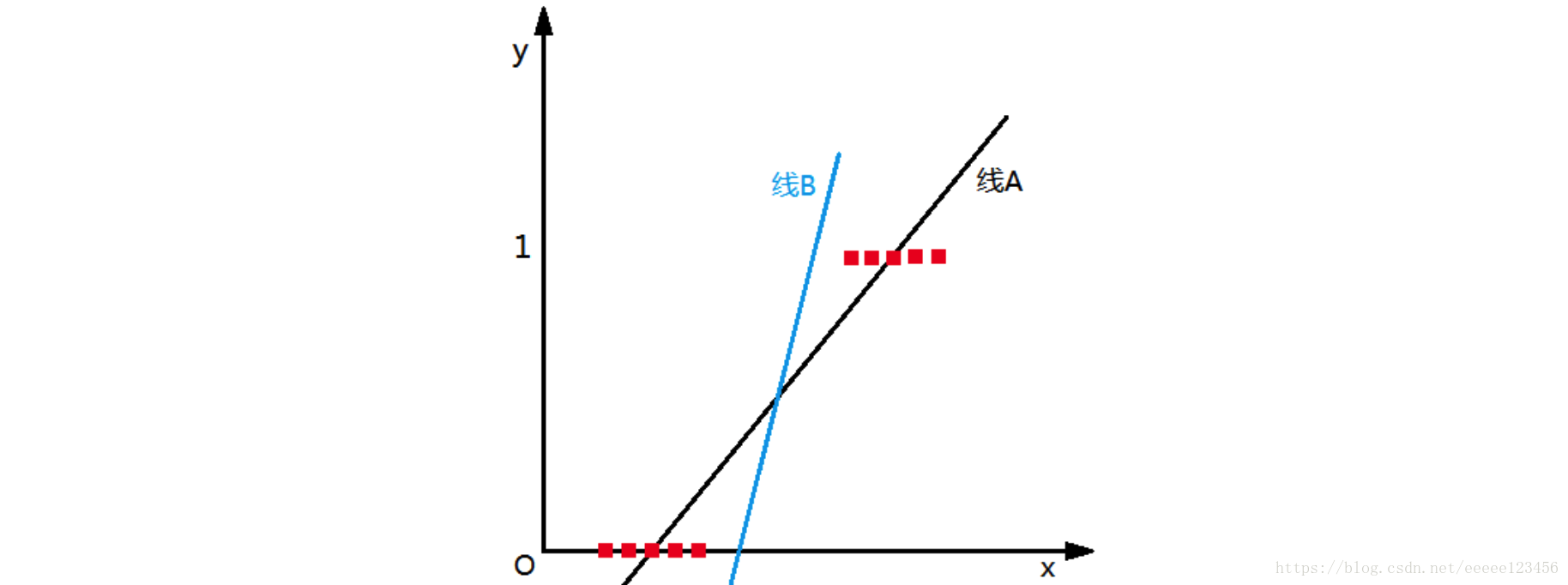
    从上图看出，线性回归模型产生的预测值 $z=w^Tx+b$是实值，于是，我们需要将实值 $z$转换为0/1值，这里我们引入Sigmoid函数，其数学形式是 $$g(z)={1\over{1+e^{-z}}}$$     图3给出了Sigmoid函数的坐标图。当 $z$为0时，Sigmoid函数值为0.5，随着 $z$的增大，对应的Sigmoid值将逼近于1；而随着 $z$的减少，Sigmoid值将逼近于0。

图3
我们将z=wTx+b代入Sigmoid函数，从而将z值转化为一个接近0或1的数，得到 $$y={1\over{1+e^{-(w^Tx+b)}}}$$

2. 模型

    逻辑回归模型所做的假设是，将(1)中$y$视为类后验估计$P(Y=1|x)$，得到

$$P(Y=1|x)={1\over{1+e^{-(w^Tx+b)}}}={e^{w^Tx+b}\over{1+e^{w^Tx+b}}}$$     通过 $P(Y=0|x)=1-P(Y=1|x)$求得 $$P(Y=0|x)={1\over{1+e^{w^Tx+b}}}$$     对于给定的实例 $x$，可以求得 $P(Y=1|x)$和 $P(Y=0|x)$，比较两个条件概率值的大小，将实例 $x$分到概率大的那一类，若概率值相等则可任意判别。

3.损失函数

    这里使用对数损失函数$L(Y,P(Y|X)) = -log P(Y|X)$。$P(Y|X)$的取值范围为[0,1]，$P(Y|X)$的值越接近1，则损失函数值越小。
    为了讨论方便，我们把w和b吸收入向量形式$\hat w=(w^T;b)^T$，令$x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)},1)^T$，则$w^Tx+b$可简写为$\hat wx$。设$P(Y=1|x)=π(x)$，$P(Y=0|x)=1-π(x)$，则最终逻辑回归模型的损失函数为

$$L(\hat w)=\sum_{i=1}^N[−y_i\logπ(x_i) −(1−y_i)\log(1−π(x_i))]$$ $$=-\sum_{i=1}^N[y_i\logπ(x_i)−y_i\log(1−π(x_i))+\log(1−π(x_i))] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$$ $$=-\sum_{i=1}^N\left[y_i\log{π(x_i)\over{1-π(x_i)}}+\log(1−π(x_i))\right] =-\sum_{i=1}^N\left[y_i({\hat w}^Tx_i)-log(1+e^{{\hat w}^Tx_i})\right]$$     对损失函数 $L(\hat w)$求极小值，从而可得 $\hat w$。
    最后求得的直线应该如图2线B，分类为0的样本点使得z<0，此时 $P(Y=1|x)<P(Y=0|x)$；分类为1的样本点使得z>0，此时 $P(Y=1|x)> P(Y=0|x)$。

4.梯度下降法

    假设$f(x$)是$R_n$上具有一阶连续偏导数的函数，要求解的无约束优化问题是

$$\min_{x∈R_n}\ \ f(x)$$ $x^*$表示目标函数 $f(x)$的极小点。
    梯度下降算法是一种迭代算法，选取适当的初值 $x^{(0)}$，不断迭代，更新 $x$的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新 $x$的值，从而达到减少函数值的目的。
    由于 $f(x)$具有一阶连续偏导数，若第 $k$次迭代值为 $x^{(k)}$，则可将 $f(x)$在 $x^{(k)}$附近进行一阶泰勒展开： $$f(x)=f(x^{(k)})+{g_k}^T(x-x^{(k)})$$ 这里， $g_k=g(x^{(k)})= ∇f(x^{(k)})$为 $f(x)$在 $x^{(k)}$的梯度。
    求出第k+1次迭代值x(k+1)： $$x^{(k+1)}=x^{(k)}+λ_kp_k$$ 其中， $p_k$是搜索方向，取负梯度方向 $p_k=-∇f(x^{(k)})$， $λ_k$是步长，由一维搜索确定，即 $λ_k$使得 $$f(x^{(k)}+λ_kp_k)=\min_{λ≥0}\ f(x^{(k)}+λp_k)$$ 算法1（梯度下降法）
输入：目标函数 $f(x)$，梯度函数 $g(x)= ∇f(x)$，计算精度 $ε$
输出： $f(x)$的极小点 $x^*$
①取初始值 $x^{(0)}∈R^n$，置 $k=0$
②计算 $f(x^{(k)})$
③计算梯度 $g_k=g(x^{(k)})$，当 $||g_k||<ε$，停止迭代，令 $x^*=x^{(k)}$；否则，令 $p_k=-∇f(x^{(k)})$，求 $λk$，使 $$f(x^{(k)}+λ_kp_k)=\min_{λ≥0}\ f(x^{(k)}+λp_k)$$ ④置 $x^{(k+1)}=x^{(k)}+λ_kp_k$，计算 $f(x^{(k+1)})$，当 $||f(x(k+1))-f(x(k))||<ε$或 $||x(k+1)-x(k)||<ε$时，停止迭代，令 $x^*=x^{(k+1)}$
⑤否则，置 $k=k+1$，转③

5.代码实现（python）

以下代码来自Peter Harrington《Machine Learing in Action》。
    我们需要求式(2)中$L(\hat w)$的最小值。若令$f(\hat w)=-L(\hat w)$，则问题可转换为求$f(\hat w)$的最大值：

$$f(\hat w)=\sum_{i=1}^N\left[y_i({\hat w}^Tx_i)-log(1+e^{{\hat w}^Tx_i})\right]$$     为了求上式的最大值，我们使用梯度上升算法。算法1（梯度下降法）中，由于与梯度相反方向下降最快，所以 $p_k=-∇f(x(k))$；而在本例的梯度上升算法，令 $p_k=∇f(x(k))$，即梯度方向上升最快。先求 $∇f(\hat w)$： $$∇f(\hat w)=\sum_{i=1}^N\left[y_ix_i-{1\over{1+e^{-{\hat w}^Tx_i}}}x_i\right]=\sum_{i=1}^Nx_i\left[y_i-{1\over{1+e^{-{\hat w}^Tx_i}}}\right]\ \ \ \ \ \ \ \ \ \ (3)$$     在本代码中，预先设置好步长 $λ$的值和迭代次数，则 $w^*=λ+∇f(\hat w)$，在循环迭代完成后输出训练好的回归系数。
代码如下（保存为logRegres.py）：

# -- coding: utf-8 --
from numpy import *

def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([float(lineArr[0]), float(lineArr[1]), 1.0]) # dataMat为吸收后的X，即将特征值最后一个元素恒置为1
        labelMat.append(int(lineArr[2])) # labelMat为对应的标记类别
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m,n = shape(dataMatrix)
    alpha = 0.001          # 步长
    maxCycles = 500        # 迭代次数
    weights = ones((n,1))  # 将w的各个元素和b初始化为1
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        # 根据式(3)可知dataMatrix.transpose()* error为梯度，则可得（新的weights）=（旧的weights）+步长＊梯度
        weights = weights + alpha * dataMatrix.transpose()* error
    return weights

数据集如下（保存为testSet.txt）：

-0.017612   14.053064   0
-1.395634   4.662541    1
-0.752157   6.538620    0
-1.322371   7.152853    0
0.423363    11.054677   0
0.406704    7.067335    1
0.667394    12.741452   0
-2.460150   6.866805    1
0.569411    9.548755    0
-0.026632   10.427743   0
0.850433    6.920334    1
1.347183    13.175500   0
1.176813    3.167020    1
-1.781871   9.097953    0
-0.566606   5.749003    1
0.931635    1.589505    1
-0.024205   6.151823    1
-0.036453   2.690988    1
-0.196949   0.444165    1
1.014459    5.754399    1
1.985298    3.230619    1
-1.693453   -0.557540   1
-0.576525   11.778922   0
-0.346811   -1.678730   1
-2.124484   2.672471    1
1.217916    9.597015    0
-0.733928   9.098687    0
-3.642001   -1.618087   1
0.315985    3.523953    1
1.416614    9.619232    0
-0.386323   3.989286    1
0.556921    8.294984    1
1.224863    11.587360   0
-1.347803   -2.406051   1
1.196604    4.951851    1
0.275221    9.543647    0
0.470575    9.332488    0
-1.889567   9.542662    0
-1.527893   12.150579   0
-1.185247   11.309318   0
-0.445678   3.297303    1
1.042222    6.105155    1
-0.618787   10.320986   0
1.152083    0.548467    1
0.828534    2.676045    1
-1.237728   10.549033   0
-0.683565   -2.166125   1
0.229456    5.921938    1
-0.959885   11.555336   0
0.492911    10.993324   0
0.184992    8.721488    0
-0.355715   10.325976   0
-0.397822   8.058397    0
0.824839    13.730343   0
1.507278    5.027866    1
0.099671    6.835839    1
-0.344008   10.717485   0
1.785928    7.718645    1
-0.918801   11.560217   0
-0.364009   4.747300    1
-0.841722   4.119083    1
0.490426    1.960539    1
-0.007194   9.075792    0
0.356107    12.447863   0
0.342578    12.281162   0
-0.810823   -1.466018   1
2.530777    6.476801    1
1.296683    11.607559   0
0.475487    12.040035   0
-0.783277   11.009725   0
0.074798    11.023650   0
-1.337472   0.468339    1
-0.102781   13.763651   0
-0.147324   2.874846    1
0.518389    9.887035    0
1.015399    7.571882    0
-1.658086   -0.027255   1
1.319944    2.171228    1
2.056216    5.019981    1
-0.851633   4.375691    1
-1.510047   6.061992    0
-1.076637   -3.181888   1
1.821096    10.283990   0
3.010150    8.401766    1
-1.099458   1.688274    1
-0.834872   -1.733869   1
-0.846637   3.849075    1
1.400102    12.628781   0
1.752842    5.468166    1
0.078557    0.059736    1
0.089392    -0.715300   1
1.825662    12.693808   0
0.197445    9.744638    0
0.126117    0.922311    1
-0.679797   1.220530    1
0.677983    2.556666    1
0.761349    10.693862   0
-2.168791   0.143632    1
1.388610    9.341997    0
0.317029    14.739025   0

调用gradAscent函数求得的值即为$\hat w$。









以上全部内容参考书籍如下：
李航《统计学习方法》
周志华《机器学习》
Peter Harrington《Machine Learing in Action》
《高等数学第六版下册 同济大学》
《数学分析简明教程 第二版上册》