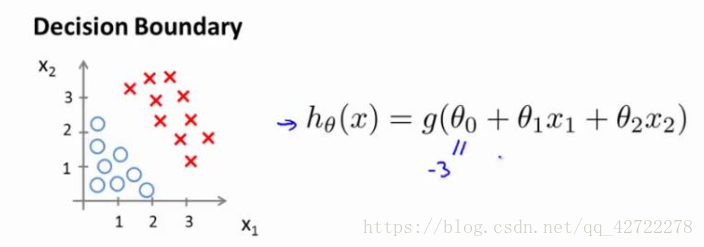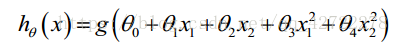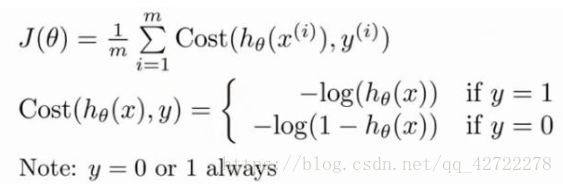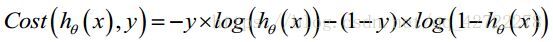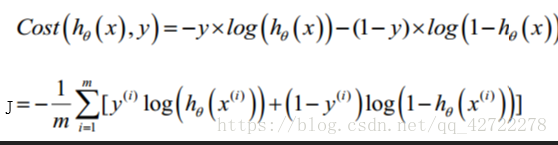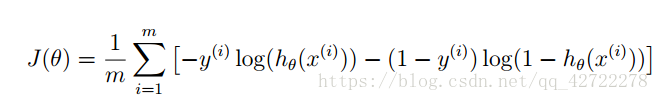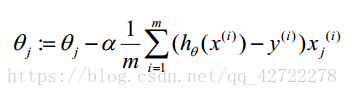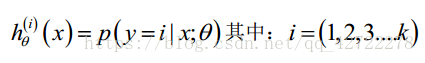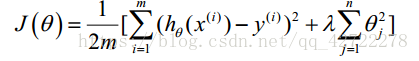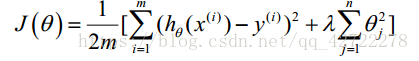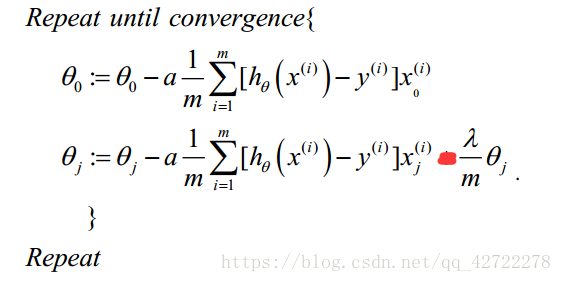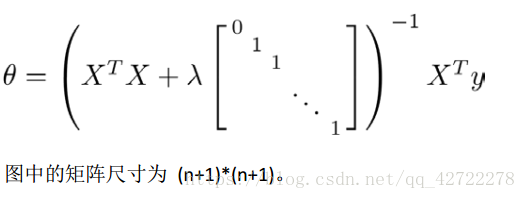机器学习之旅（三）

吴恩达教授的机器学习课程的第三周相关内容：

1、逻辑回归(Logistic Regression)

1.1、分类问题

在分类问题中，你要预测的变量 y 是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。
我们从二元的分类问题开始讨论。
我们将因变量(dependant variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量 $y\in \left \{ 0,1 \right \}$， 其中 0 表示负向类， 1 表示正向类。我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在 0 到 1 之间。
小结：逻辑回归是一种分类算法，适用于标签y取值离散的情况，如0,1,2…。

1.2、假说表示（Hypothesis Representation）

根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出 0 或 1，
我们可以预测：当 $h_{\theta }\left ( x \right )$大于等于 0.5 时，预测 y=1，当 $h_{\theta }\left ( x \right )$小于 0.5 时，预测 y=0 。
我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在 0 和 1 之间。 逻辑回归模型的假设是： $h_{\theta }\left ( x \right )=g\left (\theta ^{\top }x \right )$,
其中：X 代表特征向量、g 代表逻辑函数（logistic function）是一个常用的逻辑函数为 S 形函数（Sigmoid function），公式为：
$g\left ( z \right )=\frac{1}{1+e^{-z}}$，合起来，我们得到逻辑回归模型的假设： $h_{\theta }\left ( x \right )=\frac{1}{1+e^{-\theta ^{\top }x }}$, $h_{\theta }\left ( x \right )$ 的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1 的可能性（estimated probablity）即: $h_{\theta }\left ( x \right )=P\left (y=1 \mid x;\theta \right )$,例如， 如果对于给定的 x， 通过已经确定的参数计算得出 hθ(x)=0.7， 则表示有 70%的几率 y 为正向类，相应地 y 为负向类的几率为 1-0.7=0.3。
小结：通过Sigmoid函数将模型输出变量控制在0到1，>=0.5的取1，<0.5的取0，继而满足模型要求。

1.3、判定边界（Decision Boundary ）

在逻辑回归中，我们预测：
当 $h_{\theta }\left ( x \right )$大于等于 0.5 时，预测 y=1。
当 $h_{\theta }\left ( x \right )$小于 0.5 时，预测 y=0 。
根据上面绘制出的 S 形函数图像，我们知道当
z=0 时 g(z)=0.5
z>0 时 g(z)>0.5
z<0 时 g(z)<0.5
又 $z=\theta ^{\top }x$ ，即：
$\theta ^{\top }x$大于等于 0 时，预测 y=1， $\theta ^{\top }x$ 小于 0 时，预测 y=0
现在假设我们有一个模型：

并且参数 是向量[-3 1 1]。 则当 $-3+x_{1}+x_{2}$ 大于等于 0，即 $x_{1}+x_{2}$大于等于 3 时，模型将预测 y=1。
我们可以绘制直线 $x_{1}+x_{2}=3$，这条线便是我们模型的分界线，将预测为 1 的区域和预测为 0 的区域分隔开。

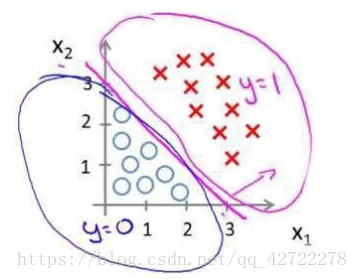
假使我们的数据呈现这样的分布情况，怎样的模型才能适合呢？

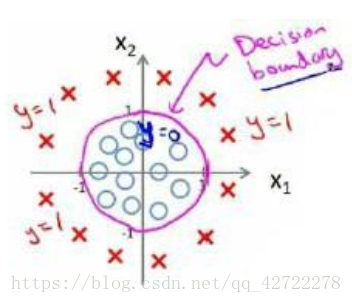
因为需要用曲线才能分隔 y=0 的区域和 y=1 的区域，我们需要二次方特征： 假设参数：

是[-1 0 0 1 1]，则我们得到的判定边界恰好是圆点在原点且半径为 1 的圆形。我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
小结：判定边界就是用来把大部分不同的数据分开，以方便更好的去预测新样本。

1.4和1.5、代价函数、简化的代价函数和梯度下降（Simplified Cost Function and Gradient Descent）

我们重新定义逻辑回归的代价函数为： ：

这个式子可以合并成：

逻辑回归的代价函数：

为了拟合出参数，我们要试图找尽量让 $J\left ( \theta \right )$取得最小值的参数 $\theta$。
最小化代价函数的方法，是使用梯度下降法(gradient descent)。这是我们的代价函数：

梯度下降算法:

小结：注意梯度下降算法表面上和线性回归的一样，但是要注意假设函数变了。

1.6、 高级优化（Advanced Optimization）

我们换个角度来看什么是梯度下降， 我们有个代价函数 $J\left ( \theta \right )$ ， 而我们想要使其最小化， 那么我们需要做的是编写代码， 当输入参数 θ 时， 它们会计算出两样东西： $J\left ( \theta \right )$ 以及 J 等于 0、 1 直到 n 时的偏导数项。

梯度下降所做的就是反复执行这些更新。另一种考虑梯度下降的思路是： 我们需要写出代码来计算 $J\left ( \theta \right )$ 和这些偏导数， 然后把这些插入到梯度下降中， 然后它就可以为我们最小化这个函数。这些算法就是为我们优化代价函数的不同方法， 共轭梯度法 BFGS (变尺度法) 和 L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法（不需要手动选择学习率 α）。对于这些算法的一种思路是，给出计算导数项和代价函数的方法，你可以认为算法有一个智能的内部循环，而且， 事实上，他们确实有一个智能的内部循环， 称为线性搜索(line search)算法， 它可以自动尝试不同的学习速率 α， 并自动选择一个好的学习速率 α。
小结：高级优化算法的简单使用和思路。

1.7、多类别分类：一对多（Multiclass Classification_ One-vs-all）

多类别的分类问题，主要思想：把其中一类设为正类，其他所有类设为负类，得出一个假设函数模型，照此循环，直到分完所有类，这个方法被称为‘一对多分类’。一系列的模型简记为：

2 、正则化(Regularization)

2.1、过拟合的问题（The Problem of Overfitting ）

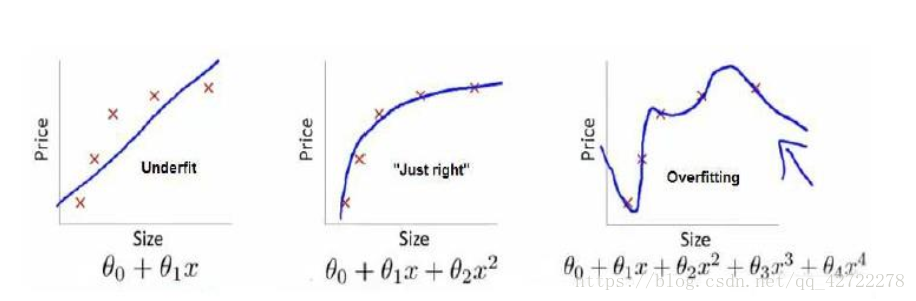
线性回归：

第一个模型是一个线性模型， 欠拟合，不能很好地适应我们的训练集；第三个模型是一个四次方的模型， 过于强调拟合原始数据，而丢失了算法的本质：预测新数据。我们可以看
出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好；而中间的模型似乎最合适。
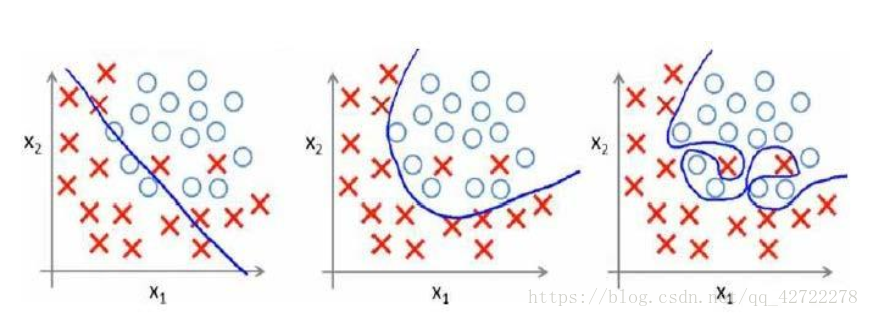
分类问题中同样也有此问题：

过拟合处理方法：

1. 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征， 或者使用
   一些模型选择的算法来帮忙（例如 PCA）
2. 正则化。 保留所有的特征，但是减少参数的大小。

2.2、代价函数

假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：

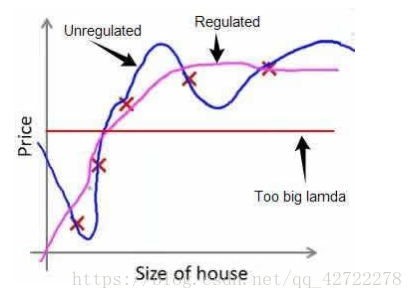
其中 $\lambda$ 又称为正则化参数（Regularization Parameter）。 注：根据惯例，我们不对 $\theta _{0}$ 进行惩罚( $\theta _{0}$作为单独的一项参与模型中)。经过正则化处理的模型与原模型的可能对比如下图所示：

小结：如果选择的正则化参数 $\lambda$过大，为了最小化代价函数， 则会把所有的参数都最小化了，导致模型变成直线，就会欠拟合。相反，则会过拟合。故 $\lambda$的取值很关键。

2.3、正则化线性回归（ Regularized Linear Regression）

正则化线性回归的代价函数为：

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对 $\theta _{0}$进行正则化，所以梯度下降算法将分两种情形：

我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下所示：

2.3、正则化的逻辑回归模型（Regularized Logistic Regression ）

代价函数和梯度下降的更新同2.2，
1.虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样，但
由于两者的 $h_{\theta }\left ( x \right )$不同所以还是有很大差别。
2. $\theta _{0}$不参与其中的任何一个正则化。

3、第三周编程题

1、sigmoid.m, g=(1+exp(-z)).^(-1),注意位运算。
2、costFunction.m,
J = -(y’log(sigmoid(Xtheta))+(1-y)‘log(1-sigmoid(Xtheta)))/m;
grad =(X’(sigmoid(Xtheta)-y))/m;
3、predict.m，p=round(sigmoid(Xtheta));round - 四舍五入为最近的小数或整数，此 MATLAB 函数 将 X 的每个元素四舍五入为最近的整数。在对等情况下，即有元素的小数部分恰为 0.5 时，round函数会偏离零四舍五入到具有更大幅值的整数。
4、costFunctionReg.m，
J=
-(y’log(sigmoid(Xtheta))+(1-y)'log(1-sigmoid(Xtheta)))/m+lambda/2/msum(theta(2:length(theta)).^2);

grad(1) =((sigmoid(X*theta)-y)'X(:,1))/m（取X的第一列）
for i=2:length(theta)
grad(i) =((sigmoid(Xtheta)-y)'X(:,i))/m+lambdatheta(i,:)/m;（取X的第i列， $\theta$的第i行）

$\theta _{0}$即octave/MATLAB中的 $\theta _{1}$不参与正则化。