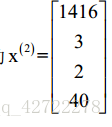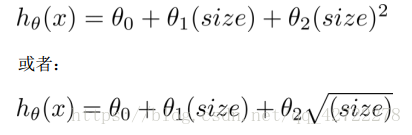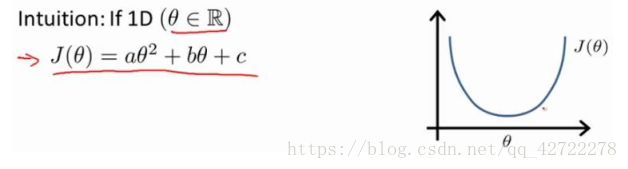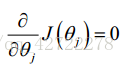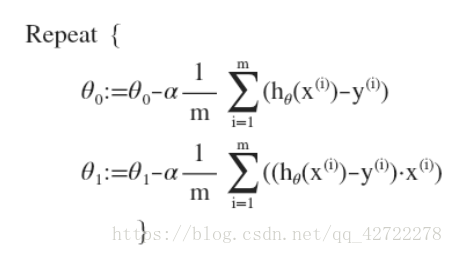机器学习之旅（二）

吴恩达教授的机器学习课程的第二周相关内容：

1、多变量线性回归(Linear Regression with Multiple Variables)

1.1、多维特征

$x_{j}^{\left ( i \right )}$代表特征矩阵中第 i 行的第 j 个特征，也就是第 i 个训练实例的第 j 个特征.
支持多变量的假设 h 表示为： $h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}$,这个公式中有 n+1 个参数和 n 个变量，为了使得公式能够简化一些，引入 $x_{0}=1$，则公式转化为： $h_{\theta }\left ( x \right )=\theta_{0}x_{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}$
此时模型中的参数是一个 n+1 维的向量，任何一个训练实例也都是 n+1 维的向量，特征矩阵 X 的维度是 m*(n+1)。 因此公式可以简化为： $h_{\theta }\left ( x \right )=\theta ^{\top }x$， 其中上标 T 代表矩阵转置。
注意：这里的x表示矩阵X的某一行，例如：

1.2、多变量梯度下降

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即: $J\left ( \theta _{0},\theta _{1},...,\theta _{n} \right )=\frac{1}{2m}\sum_{i=1}^{m}\left (h _{\theta }\left (x ^{\left ( i \right )} \right )- (y ^{\left ( i \right )}\right )^{2}$
其中： $h_{\theta }\left ( x \right )=\theta ^{\top }x=\theta_{0}x_{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}$
我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。
多变量线性回归的批量梯度下降算法为

我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

1.3、梯度下降法实践 1-特征缩放

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。
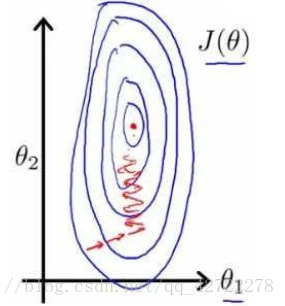
以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000 平方英尺，而房间数量的值则是 0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能， 看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。通常我们所用的方法是令: $x_{n}=\frac{x_{n}-\mu _{n}}{s_{n}}$,其中 $\mu _{n}$是平均值, $s_{n}$是标准差，即：

1.4 梯度下降法实践 2-学习率

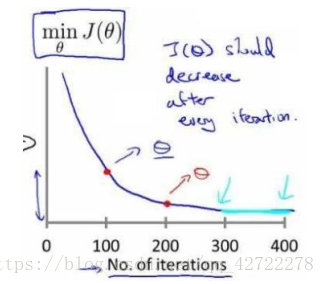
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

梯度下降算法的每次迭代受到学习率的影响， 如果学习率 α 过小， 则达到收敛所需的迭代次数会非常高； 如果学习率 α 过大， 每次迭代可能不会减小代价函数， 可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率：
α=0.01， 0.03， 0.1， 0.3， 1， 3， 10

1.5 特征和多项式回归

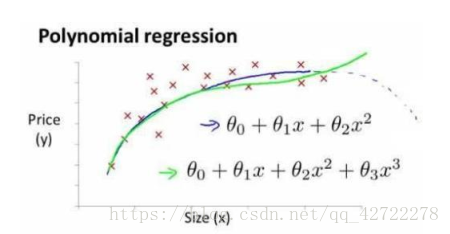
线性回归并不适用于所有数据，有时我们需要曲线来适应我们的数据，比如一个二次方模型： $h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}^{2}$
或者三次方模型： $h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}^{2}+\theta _{3}x_{3}^{3}$

通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外，我们可以令： $x_{2}=x_{2}^{2} ,x_{3}=x_{3}^{3}$
从而将模型转化为线性回归模型。根据函数图形特性，我们还可以使：

小结：一定要先观察数据分布再决定准备尝试模型，如果我们采用多项式回归模型，在运行梯度下降算法前， 特征缩放非常有必要。

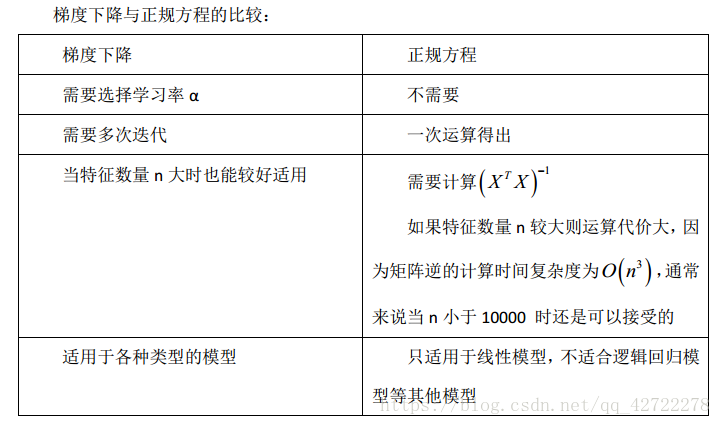
1.6 正规方程

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。 如：

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：

也就是求其切线斜率为0的地方。
假设我们的训练集特征矩阵为 X（包含了 $x_{0}=1$）并且我们的训练集结果为向量 y，则利用正规方程解出向量 $\theta =\left ( X^{\top }X \right )^{-1} X^{\top }y$。
上标 T 代表矩阵转置，上标-1 代表矩阵的逆。

小结：只要特征变量的数目并不大，标准方程是一个很好的计算参数 $\theta$ 的替代方法。具体地说，只要特征变量数量小于一万，通常使用标准方程法，而不使用梯度下降法。随着我们要讲的学习算法越来越复杂，对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法，我们将不得不仍然使用梯度下降法。
至于正规方程的推导过程可以看看这两篇文章分介绍正规方程推导1、正规方程推导2。

1.7octave/MATLAB的一些基本操作

这里给出总结的比较好的博客链接基操。

1.8 第二周的编程题

1、 warmUpExercise.m,这里主要是为了练习作业的提交，输入A=eye(5);产生一个5x5的单位方阵就可以通过了。
2、computeCost.m,这是让你用向量化的代码实现计算代价函数，由 $h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x$以及
$J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{2m}\sum_{i=1}^{m}\left (h _{\theta }\left (x ^{\left ( i \right )} \right )- (y ^{\left ( i \right )}\right )^{2}$
得：

3、gradientDescent.m,求单变量的梯度下降算法，由

得：

4、featureNormalize.m,这是主要针对多变量的特征缩放，由 $x_{n}=\frac{x_{n}-\mu _{n}}{s_{n}}$可得,
mu=mean(X_norm);求平均值
sigma=std(X_norm);求方差
X_norm=(X_norm-mu)./sigma;特征缩放后的结果（.代表位运算）

5、computeCostMulti.m思路和结果都同2，这里就是X和 $\theta$的列改变了。

6、gradientDescentMulti.m思路和结果都同3，这里就是X和 $\theta$的列改变了。

7、normalEqn.m通过正规方程来求 $\theta$，由 $\theta =\left ( X^{\top }X \right )^{-1} X^{\top }y$，则

以上内容仅代表个人观点，如有错误，望多多指教。