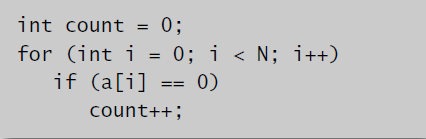【算法】算法分析

相关资料来源于网络，侵删歉。
如果文章中存在错误，请下方评论告知我，谢谢！

用科学的方法分析算法

观察真实世界的特征；
根据观察提出假设模型；
根据模型预测未来的事件；
继续观察验证预测的准确性；
反复如此直到确认预测和观察一致。

原则

实验必须是可重现的；
假设必须是可验证的。

接下来，我们将利用上述方法解决一个经典问题。

3-Sum问题
给定N个不同的整数，问有多少个三元组其和恰好为零？

初步解决方法是暴力求解，利用三层循环遍历所有情况，代码如下：

public class ThreeSum
{
    public static int count(int[] a)
    {
        int N = a.length;
        int count = 0;
        for (int i = 0; i < N; i++)
            for (int j = i+1; j < N; j++)
                for (int k = j+1; k < N; k++)
                    if (a[i] + a[j] + a[k] == 0)
                        count++;
        return count;
    }

    public static void main(String[] args)
    {
        int[] a = In.readInts(args[0]);
        StdOut.println(ThreeSum.count(a));
    }
}

这种方法的效率怎么样呢？我们需要用时间来衡量。因此，我们需要有一个计时器。

public class Stopwatch
{
	private final long start;
	public Stopwatch()
	{ start=System.currentTimeMillis(); }
	public double elapsedTime()
	{
		long now=System.currentTimeMillis();
		return (now-start)/1000.0;
	}
}

然后我们修改算法程序，使其能够自动计时。

public class ThreeSum
{
    public static int count(int[] a)
    {
        int N = a.length;
        int count = 0;
        for (int i = 0; i < N; i++)
            for (int j = i+1; j < N; j++)
                for (int k = j+1; k < N; k++)
                    if (a[i] + a[j] + a[k] == 0)
                        count++;
        return count;
    }

    public static void main(String[] args)
    {
        int[] a = In.readInts(args[0]);
        Stopwatch stopwatch = new Stopwatch();
        StdOut.println(ThreeSum.count(a));
        double time = stopwatch.elapsedTime();
    }
}

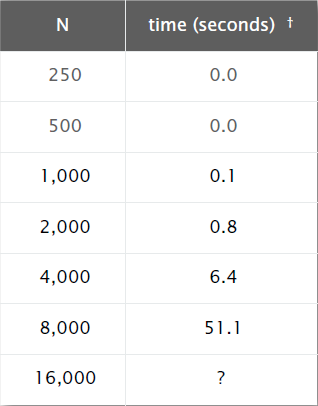
于是我们得到了测试数据规模与程序运行时间的关系表格。

通过这张表格，我们大致可以看出，每当N增长1倍时，运行时间大概增长8倍。当N=16000时，由于长时间未出现结果，不知道还要等待多长时间，于是匆匆结束了测试。
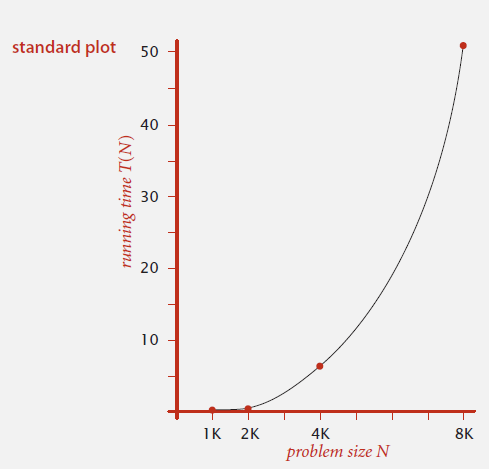
我们再以绘图的形式，分析一下N与运行时间呈现怎样的关系。

通过图像，我们大概猜测N与运行时间呈现幂次的关系，即 $T(N)=aN^{b}$ 。是这样吗？
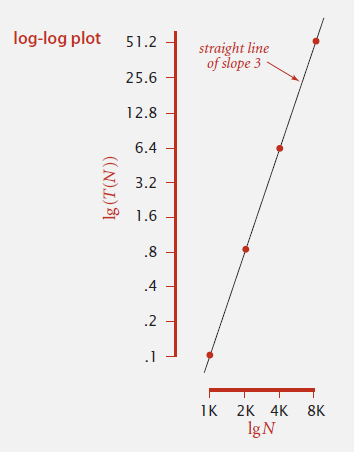
我们通过对数函数图像来验证一下。

图像近似是一条直线，我们求出这条直线的表达式。（注：log和lg两者在算法中的使用存在混淆，但都是以2为底的对数）
$log(T(N)) = blogN+c$
$b=2.999,c=-33.2103$
$\Rightarrow T(N)=aN^{b}, a=2^{c}$
这与我们猜测的一致。
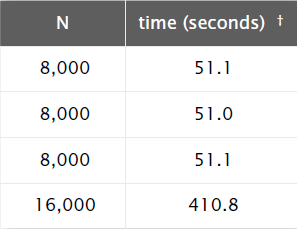
现在用数据说话，我们将N=8000代入得T=51.06，再代入N=16000得T=408.19。
我们以这两种数据规模运行一下程序，发现实际运行时间与计算得到的时间相差无几。

之后，我们经过反复测试，认定上述推理能较准确的描述两者的关系。
（注：在实际生活中，我们的推理可能不会太严谨。我们大致猜测出数学模型，并通过计算快速得到其对应的系数，再作简单验证。）

除了时间，算法对计算机内存的占用空间也是作为我们衡量算法效率的一个重要指标。但在如今社会，计算机的内存已经相当大了，我们的程序基本都可以在有限的内存空间下执行结束，所以，我们暂且忽略算法的占用空间问题，只考虑时间的快慢，毕竟时间在大多是情况下都是非常宝贵的。

在计算机科学早期，D.E.Knuth认为，尽管有许多复杂的因素影响着我们对程序运行时间的计算，但原则上我们仍然可能构造出一个数学模型来描述任何程序的运行时间。他的思路是，一个程序运行的时间主要和两点有关：

执行每条语句的耗时
执行每条语句的频率

前者取决于计算机硬件、操作系统和编译系统，后者取决于程序代码本身。
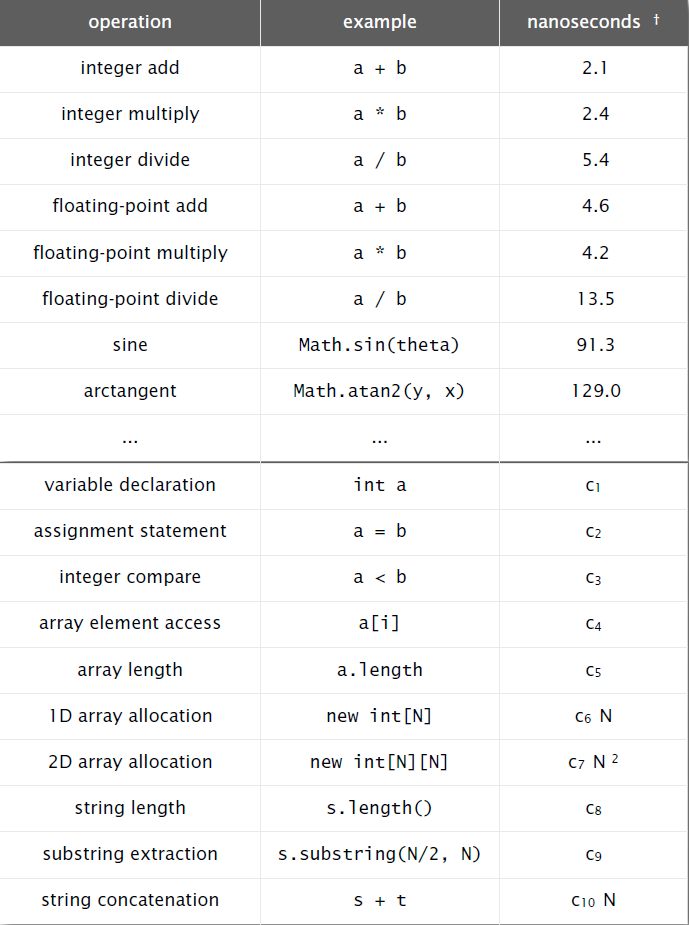
下面的表格列出了一些基本操作在某台计算机上的执行时间。

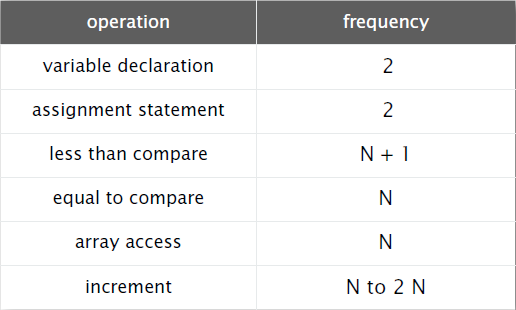
我们再来分析一些程序的语句执行频率。

相等比较的次数：从N个数中任选2个数，即组合数 $\binom{N}{2}=\frac{1}{2}N(N-1)$ ；
递增操作的次数：最少：i递增N次，j递增(N-1)+(N-2)+...+2+1+0次，共 $\frac{1}{2}N(N-1)$ 次；最多：i递增，j递增，count递增 $\binom{N}{2}$ 次，共 $N(N-1)$ 次。

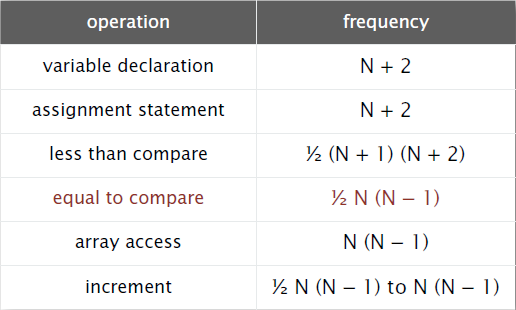
因为每条语句的执行时间难以计算，所以我们简化模型，假设每条语句的执行时间相同，都为1个单位。
这样，我们可以将每种操作的执行频率相加，就得到程序的运行时间。

这种频率相加会产生复杂冗长的数学表达式，我们分析得知，
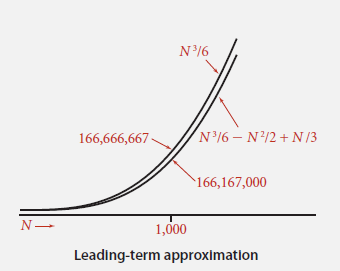
当N较大时，我们忽略次数较小的项，只得到一个次数最大的项。例如：
$\frac{1}{6}N^{3}-\frac{1}{2}N{}^{2}+\frac{1}{3}N$ ，可以近似为 $\frac{1}{6}N^{3}$ 。
两者在N很大时，相差并不是很多。在N很小时，因为运行时间很短，也可以忽略两者的差别。
我们可以通过函数图像来比较两者，可以看到两者的曲线形状相似，距离相近。

所以这种近似是较合理的。

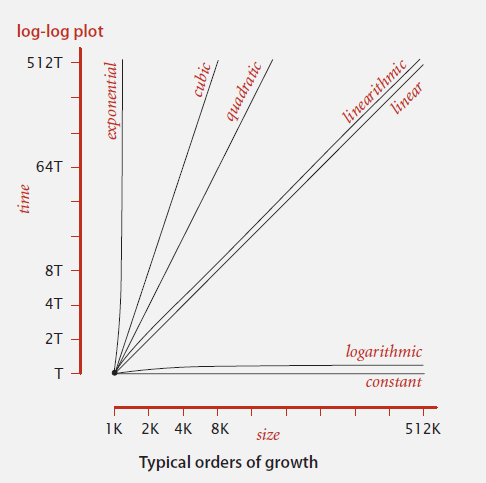
在算法中，时间有下面几种增长级别：
常数：1
对数级：logN
线性级：N
线性对数级：NlogN
平方级：N²
立方级：N³
指数级：2^N

我们通过函数图像来作比较：

常量级和对数级的算法，可用于解决大规模数据的问题；
线性级和线性对数级的算法，可用于解决普通规模数据的问题；
平方级和立方级的算法，解决普通规模数据的问题显得有些吃力了；
指数级的算法，即使是很小规模数据的问题都有些吃力。

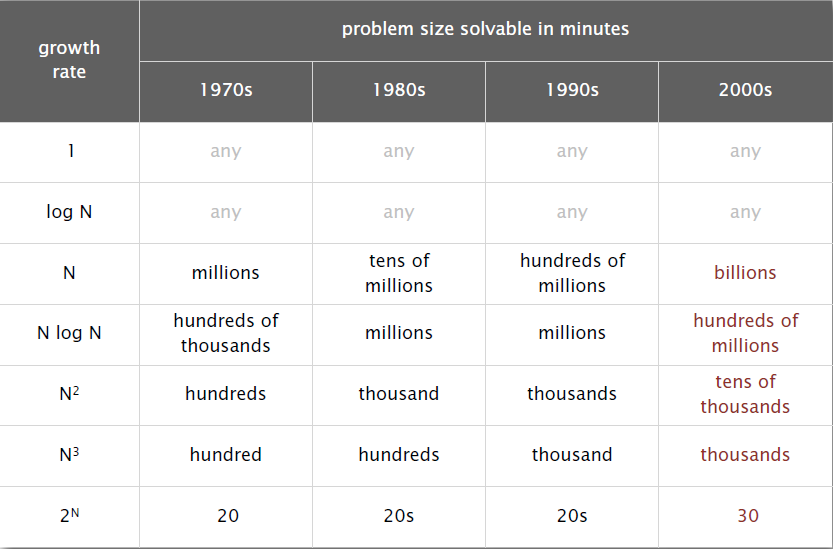
通过下面这种表，我们可以感性地认识一下各种增长极的解决问题能力：

【算法】算法分析

猜你喜欢