一文读懂正则化与LASSO回归，Ridge回归

一、过拟合

当样本特征很多，样本数相对较少时，模型容易陷入过拟合。为了缓解过拟合问题，有两种方法：

方法一：减少特征数量（人工选择重要特征来保留，会丢弃部分信息）。

方法二：正则化（减少特征参数 $w$ 的数量级）。

二、正则化（Regularization）

正则化是结构风险（损失函数+正则化项）最小化策略的体现，是在经验风险（平均损失函数）上加一个正则化项。正则化的作用就是选择经验风险和模型复杂度同时较小的模型。

防止过拟合的原理：正则化项一般是模型复杂度的单调递增函数，而经验风险负责最小化误差，使模型偏差尽可能小。经验风险越小，模型越复杂，正则化项的值越大。要使正则化项也很小，那么模型复杂程度受到限制，因此就能有效地防止过拟合。

三、线性回归正则化（Regularized Linear Regression）

正则化一般具有如下形式的优化目标：

$\mathop {\min }\limits_{f \in F} \left[ {\frac{1}{m}\sum\limits_{i = 1}^m {L\left( {{y_i},f\left( {{x_i}} \right)} \right)} + \lambda J\left( f \right)} \right]$ (1)

其中， $\lambda \geq 0$ 是用来平衡正则化项和经验风险的系数。

正则化项可以是模型参数向量的范数，经常用的有 $L_1$ 范数、 $L_2$ 范数（ $L_1$ 范数： ${\left\| x \right\|_1} = \sum\limits_{i = 1}^m {\left| {{x_i}} \right|}$ ， $L_2$ 范数： ${\left\| x \right\|_2} = \sqrt {\sum\limits_{i = 1}^m {x_i^2} }$ ）。

我们考虑最简单的线性回归模型。

给定数据集给定数据集 $D = \left\{ {\left( {{x_i},{y_i}} \right)} \right\}_{i = 1}^m$ ，其中 $x_i=\left( {{x_{i1}},{x_{i2}}, \ldots ,{x_{id}}} \right)$ ， ${y_i} \in R$ 。

代价函数为： $J\left( w \right) = \frac{1}{m}{\left\| {y - {w^T}X} \right\|^2} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {w^T}{x_i}} \right)}^2}}$ (2)

（1） $L_2$ 范数正则化（Ridge Regression，岭回归）

代价函数为： $J\left( w \right) = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {w^T}{x_i}} \right)}^2}} + \lambda \left\| w \right\|_2^2\left( {\lambda > 0} \right)$ (3)

（2） $L_1$ 范数正则化（LASSO，Least Absolute Shrinkage and Selection Operator）

代价函数为： $J\left( w \right) = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {w^T}{x_i}} \right)}^2}} + \lambda {\left\| w \right\|_1}\left( {\lambda > 0} \right)$ (4)

（3） $L_1$ 正则项和 $L_2$ 正则项混合使用（Elastic Net）

代价函数为： $J\left( w \right) = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {w^T}{x_i}} \right)}^2}} + \lambda \left( {\rho {{\left\| w \right\|}_1} + \left( {1 - \rho } \right)\left\| w \right\|_2^2} \right)$ (5)

其中， $L_1$ 范数和 $L_2$ 范数正则化都有助于降低过拟合风险， $L_2$ 范数通过对参数向量各元素平方和求平方根，使得 $L_2$ 范数最小，从而使得参数 $w$ 的各个元素都接近0，但不等于0。而 $L_1$ 范数正则化比 $L_2$ 范数更易获得“稀疏”解，即 $L_1$ 范数正则化求得的 $w$ 会有更少的非零分量，所以 $L_1$ 范数可用于特征选择，而 $L_2$ 范数在参数规则化时经常用到。（事实上， $L_0$ 范数得到的“稀疏”解最多，但 $L_0$ 范数 $\left\| x \right\| = \# \left( {i\left| {{x_i} \ne 0} \right.} \right)$ 是向量中非零元素的个数，不连续，难以优化求解。因此常用 $L_1$ 范数来近似）。

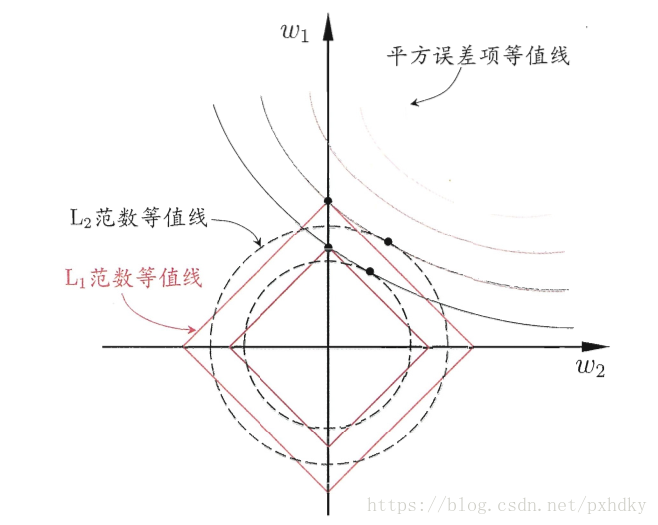
为什么 $L_1$ 正则化更易获得“稀疏”解呢？

假设 $x$ 仅有两个属性， $w$ 只有两个参数 ${w_1},{w_2}$ ，绘制不带正则项的目标函数——平方误差项等值线，再绘制 $L_1$ 、 $L_2$ 范数等值线，如图1。正则化后优化目标的解要在平方误差项和正则化项之间折中，即出现在图中等值线相交处。采用 $L_1$ 范数时，交点常出现在坐标轴上，即 ${w_1}$ 或 ${w_2}$ 为0；而采用 $L_2$ 范数时，交点常出现在某个象限中，即 ${w_1}$ ， ${w_2}$ 均非0。也就是说， $L_1$ 范数比 $L_2$ 范数更易获得“稀疏”解。

四、Ridge回归求解

Ridge回归不抛弃任何一个特征，缩小了回归系数。

Ridge回归求解与一般线性回归一致。

（1）如果采用梯度下降法：

$\frac{{\partial J\left( w \right)}}{{\partial {w_j}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{w^T}{x_i} - {y_i}} \right){x_{ij}} + 2\lambda {w_j}}$ (6)

迭代公式如下：

$\begin{array}{l} {w_{j + 1}} = {w_j} - \frac{\alpha }{m}\sum\limits_{i = 1}^m {\left( {{w^T}{x_i} - {y_i}} \right){x_{ij}} - 2\lambda {w_j}} \\ = \left( {1 - 2\lambda } \right){w_j} - \frac{\alpha }{m}\sum\limits_{i = 1}^m {\left( {{w^T}{x_i} - {y_i}} \right){x_{ij}}} \end{array}$ (7)

（2）如果采用正规方程：

最优解为：

${w^*} = {\left( {{X^T}X + \lambda I} \right)^{ - 1}}{X^T}y$ (8)

最后，将学得的线性回归模型为:

$\widehat y = {w^T}X = {X^T}w = {\left( {{X^T}X + \lambda I} \right)^{ - 1}}{X^T}y$ (9)

五、LASSO回归求解

由于 $L_1$ 范数用的是绝对值之和，导致LASSO的优化目标不是连续可导的，也就是说，最小二乘法、梯度下降法、牛顿法、拟牛顿法都不能用。

$L_1$ 正则化问题求解可采用近端梯度下降法（Proximal Gradient Descent,PGD）。

（1）优化目标

优化目标为： $\mathop {\min }\limits_x \left[ {f\left( x \right) + \lambda {{\left\| x \right\|}_1}} \right$ (10)

若 ${f\left( x \right)}$ 可导，且梯度 $\nabla f\left( x \right)$ 满足L-lipschitz（利普希茨连续条件），即存在常数 $L>0$ ，使得：

$\frac{{\left\| {\nabla f\left( {x'} \right) - \nabla f\left( x \right)} \right\|_2^2}}{{\left\| {x' - x} \right\|_2^2}} \le L,\forall \left( {x,x'} \right)$ (11)

L-lipschitz（利普希茨连续条件）定义：

对于函数 $f\left( x \right)$ ，若其任意定义域中的 $x_1$ ， $x_2$ ，都存在 $L>0$ ，使得 $\left| {f\left( {{x_1}} \right) - f\left( {{x_2}} \right)} \right| \le L\left| {{x_1} - {x_2}} \right|$ ，即对于 $f\left( x \right)$ 上每对点，链接它们的线的斜率的绝对值总是不大于这个实数 $L$ 。

（2）泰勒展开

则在 $x_k$ 附近可将 $f\left( x \right)$ 进行二阶泰勒展开：

$f\left( x \right) = f\left( {{x_k}} \right) + \nabla f\left( {{x_k}} \right)\left( {x - {x_k}} \right) + \frac{{f''\left( {{x_k} + \xi } \right)}}{2}{\left( {x - {x_k}} \right)^2}$ (12)

由（11）式，将泰勒展开式的二阶导用 $L$ 近似代替，得到：

$f\left( x \right) \approx f\left( {{x_k}} \right) + \nabla f\left( {{x_k}} \right)\left( {x - {x_k}} \right) + \frac{L}{2}{\left( {x - {x_k}} \right)^2}$ (13)

（3）简化泰勒展开式

将（13）式化简：

$\begin{array}{l} f\left( {{x_k}} \right) + \nabla f\left( {{x_k}} \right)\left( {x - {x_k}} \right) + \frac{L}{2}{\left( {x - {x_k}} \right)^2}\\ = \frac{L}{2}\left[ {{{\left( {x - {x_k}} \right)}^2} + \frac{2}{L}\nabla f\left( {{x_k}} \right)\left( {x - {x_k}} \right) + \frac{1}{{{L^2}}}{{\left( {\nabla f\left( {{x_k}} \right)} \right)}^2}} \right] - \frac{L}{2}\frac{1}{{{L^2}}}{\left( {\nabla f\left( {{x_k}} \right)} \right)^2} + f\left( {{x_k}} \right)\\ = \frac{L}{2}{\left[ {x - \left( {{x_k} - \frac{1}{L}\nabla f\left( {{x_k}} \right)} \right)} \right]^2} + \varphi \left( {{x_k}} \right)\\ = \frac{L}{2}\left\| {x - \left( {{x_k} - \frac{1}{L}\nabla f\left( {{x_k}} \right)} \right)} \right\|_2^2 + \varphi \left( {{x_k}} \right) \end{array}$ (14)

其中， $\varphi \left( {{x_k}} \right){\rm{ = }}f\left( {{x_k}} \right) - \frac{1}{{2L}}{\left( {\nabla f\left( {{x_k}} \right)} \right)^2}$ 是与 $x$ 无关的常数。

（4）简化优化问题

这里若通过梯度下降法对 $f\left( x \right)$ （ $f\left( x \right)$ 连续可导）进行最小化，则每一步下降迭代实际上等价于最小化二次函数 $\widehat f\left( x \right)$ ，推广到优化目标（10），可得到每一步迭代公式：

${x_{k + 1}} = \mathop {\arg \min }\limits_x \left[ {\frac{L}{2}\left\| {x - \left( {{x_k} - \frac{1}{L}\nabla f\left( {{x_k}} \right)} \right)} \right\|_2^2 + \lambda {{\left\| x \right\|}_1}} \right]$ (15)

令 $z = {x_k} - \frac{1}{L}\nabla f\left( {{x_k}} \right)$ ，

则可以先求 $z$ ，再求解优化问题：

${x_{k + 1}} = \mathop {\arg \min }\limits_x \left[ {\frac{L}{2}\left\| {x - z} \right\|_2^2 + \lambda {{\left\| x \right\|}_1}} \right]$ (16)

（5）求解

令 $x^i$ 为 $x$ 的第 $i$ 个分量，将（16）式按分量展开，其中不存在 $x^ix^j(i\neq j)$ 这样的项，即 $x$ 的各分量之间互不影响，所以12）式有闭式解。

为什么（16）式不存在 $x^ix^j(i\neq j)$ 这样的项？

因为展开（16）式得到， $\begin{array}{l} \mathop {\arg \min }\limits_x \left[ {\frac{L}{2}\left\| {x - z} \right\|_2^2 + \lambda {{\left\| x \right\|}_1}} \right]\\ = \mathop {\arg \min }\limits_x \left( {\frac{L}{2}\left\| {{x^1} - {z^1}} \right\|_2^2 + \lambda {{\left\| {{x^1}} \right\|}_1}} \right) + \mathop {\arg \min }\limits_x \left( {\frac{L}{2}\left\| {{x^2} - {z^2}} \right\|_2^2 + \lambda {{\left\| {{x^2}} \right\|}_1}} \right) + \cdots \\ + \mathop {\arg \min }\limits_x \left( {\frac{L}{2}\left\| {{x^d} - {z^d}} \right\|_2^2 + \lambda {{\left\| {{x^d}} \right\|}_1}} \right) \end{array}$

从而优化问题变为求解d个独立的函数： $f\left( x \right) = {\left( {x - z} \right)^2} + \lambda {\left\| x \right\|_1}$ 。

对于上述优化问题需要用到soft thresholding软阈值函数（证明见参考文献2），即对于优化问题：

$\mathop {\arg \min }\limits_x \left[ {\left\| {x - z} \right\|_2^2 + \lambda {{\left\| x \right\|}_1}} \right]$ (17)

其解为： $pro{x_u}\left( z \right) = sign\left( z \right)\max \left\{ {\left| z \right| - u,0} \right\}$ (18)

而我们的优化问题为（16）式，则得到闭式解为：

$x_{k + 1}^i = \left\{ {\begin{array}{*{20}{c}} {{z^i} - \frac{{2\lambda }}{L}}&,&{{z^i} > \frac{{2\lambda }}{L}}\\ 0&,&{ - \frac{{2\lambda }}{L} < {z^i} < \frac{{2\lambda }}{L}}\\ {{z^i} + \frac{{2\lambda }}{L}}&,&{{z^i} < - \frac{{2\lambda }}{L}} \end{array}} \right\}$ (19)

其中， $x_{k + 1}^i$ 与 $z^i$ 分别是 $x_{k + 1}$ 与 $z$ 的第 $i$ 个分量。因此，通过PGD能是LASSO和其他基于 $L_1$ 范数最小化的方法得以快速求解。

参考文献：

1. 《机器学习》第十一章嵌入式选择与L1正则化-周志华

2. LASSO回归与L1正则化西瓜书

3. 机器学习之正则化（Regularization）

4. 正则化及正则化项的理解