0. 前言

支持向量机SVM（Support Vector Machine）可以用于分类和回归。SVM将向量映射到高维空间中，在空间中建立一个最大间隔的超平面，这个超平面两边建有两个相互平行的分开数据的超平面，使得其与中间的超平面距离最大化。

1. 代价函数（Cost Function）

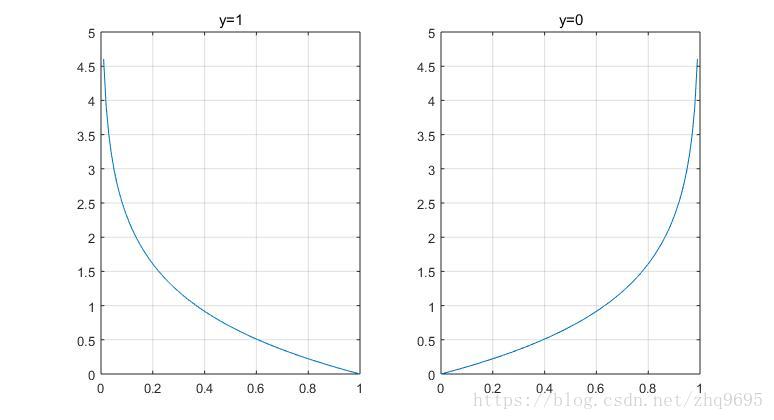
在逻辑回归中，代价函数为 $J(\theta)= -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_{j}^{2}$ ，其中 $y=1\ y=0$ 的代价函数如下所示：

扫描二维码关注公众号，回复： 3484960 查看本文章

如果对其进行修改，SVM的代价函数如下定义：

$\large \begin{align*} J(\theta)= C\sum_{i=1}^{m}[y^{(i)}Cost_{1}(\theta^{T}x^{(i)})+(1-y^{(i)})Cost_{0}(\theta^{T}x^{(i)})]+\frac{1}{2}\sum_{j=1}^{n}\theta_{j}^{2} \end{align*}$

其中， $C$ 是一个类似权重的系数， $Cost_{1}(\theta^{T}x)\ Cost_{0}(\theta^{T}x)$ 的函数如下所示：

则对代价函数的要求如下：

$\large \left\{\begin{align*} &if\ y=1\Rightarrow \theta^{T}x\geqslant 1\\ &if\ y=0\Rightarrow \theta^{T}x\leqslant -1 \end{align*}\right.$

注：如果 $C$ 太大，造成代价函数第一部分值小，第二部分值较大，造成过拟合（对异常点敏感）。

2. 假设函数（Hypothesis）

$\large h_{\theta}(x)= \left\{\begin{align*} &1\ ,\ if\ \theta^{T}x\geqslant 0\\ &0\ ,\ else \end{align*}\right.$

3. 范数表示

设向量 $u=\begin{bmatrix} u_{1}\\ u_{2} \end{bmatrix}\ v=\begin{bmatrix} v_{1}\\ v_{2} \end{bmatrix}$ ，如下图所示（图源：吴恩达机器学习）：

$\begin{Vmatrix} u \end{Vmatrix} =\sqrt{u_{1}^{2}+u_{2}^{2}}$ 称为范数， $p$ 为 $v$ 在 $u$ 上的投影长度，满足 $u^{T}v=p\cdot \begin{Vmatrix} u \end{Vmatrix}$ 。

所以，代价函数的第二部分可以如下表示：

$\large \frac{1}{2}\sum_{j=1}^{n}\theta_{j}^{2}=\frac{1}{2}(\theta_{1}^{2}+...+\theta_{n}^{2})=\frac{1}{2}\sqrt{\theta_{1}^{2}+...+\theta_{n}^{2}}^{2}=\frac{1}{2}\begin{Vmatrix} \theta \end{Vmatrix}^{2}$

代价函数的要求可表示为：

$\large \left\{\begin{align*} &if\ y=1\Rightarrow p\cdot\begin{Vmatrix} \theta \end{Vmatrix}\geqslant 1\\ &if\ y=0\Rightarrow p\cdot\begin{Vmatrix} \theta \end{Vmatrix}\leqslant -1 \end{align*}\right.$

4. 高斯核函数（Gaussian Kernel）

已知，在线性SVM中，计算的是 $\theta^{T}x$ ，如果对其进行修改，计算 $\theta^{T}f$ ，则是高斯核函数的SVM， $f$ 的定义如下：

$\large \begin{align*} f_{1}&=similarity(x,l^{(1)})=exp(-\frac{\begin{Vmatrix} x-l^{(1)} \end{Vmatrix}^{2}}{2\sigma ^{2}})\\ f_{2}&=similarity(x,l^{(2)})=exp(-\frac{\begin{Vmatrix} x-l^{(2)} \end{Vmatrix}^{2}}{2\sigma ^{2}})\\ ... \end{align*}$

其中， $\large l$ 称为标记点， $\large l^{(1)},l^{(2)},...,l^{(m)}$ ，每一个标记点与每一个样本数据在空间中位于相同位置。所以有：

如果 $x$ 与 $l$ 相近 $\Rightarrow f\approx exp(0)\approx1$
如果 $x$ 与 $l$ 相隔远 $\Rightarrow f=exp(-\infty )\approx0$

高斯核函数的SVM流程可表示为：

给定数据集 $(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})$
设 $l^{(1)}=x^{(1)},...,l^{(m)}=x^{(m)}$
对于测试样本 $x$ ，计算 $f=\begin{bmatrix} f_{1}\\ ...\\ f_{m} \end{bmatrix}$
$\theta^{T}f\geqslant 0\Rightarrow y=1\ ,\ \theta^{T}f\leqslant 0\Rightarrow y=0$

此时代价函数修改为：

$\large \begin{align*} J(\theta)= C\sum_{i=1}^{m}[y^{(i)}Cost_{1}(\theta^{T}f^{(i)})+(1-y^{(i)})Cost_{0}(\theta^{T}f^{(i)})]+\frac{1}{2}\sum_{j=1}^{n}\theta_{j}^{2} \end{align*}$