EM算法及高斯混合模型（含Mathematica实现代码）

模式识别课程中已经学习了EM算法和高斯混合模型，但是听课的时候感觉十分茫然，课程中乃至的概率论等内容和数学中的内容有些脱节，直接套用数学中的内容甚至会导致前后矛盾。课后反复研究之后，发现是不正规的甚至是错误的数学语言的使用导致的公式晦涩难懂。因此在此做一些笔记，努力让公式简单一些。

高斯混合模型

从一个例子说起。

一片树林中有A、B、C三种树木，每种树木的叶子的面积与最大宽度分别服从联合高斯分布（具体参数未知）。如何通过收集一定量的树叶（不知道这些树叶属于哪种树木），试对这些树叶进行分类，并估算出三种树木的联合高斯分布的参数。

首先要对这个例子进行数学描述。每个叶子可以用一个二维向量表示： $\mathbf{x}=(x_1,x_2)$ ，其中的 $x_1,x_2$ 分别为树叶的面积和最大宽度。叶子属于哪种树用三维向量表示： $\mathbf{z}=(z_1,z_2,z_3)$ ，其中， $z_1,z_2,z_3$ 中有且仅有一个为1，其余两个为0. $z_1$ 为1表示该树叶属于树木A， $z_2,z_3$ 与此含义相同。总共采集了 $m=100$ 片叶子，则第 $i$ 片叶子记为 $\mathbf{x}_i$ ，类别为 $\mathbf{z}_i$ ，对于 $\mathbf{z}_i$ ， $z^{(i)}$ 表示 $\mathbf{z}_i$ 中第几个分量为1，比如，若 $\mathbf{z}_5=(0,1,0)$ ，则 $z^{(5)}=2$ 。树A、B、C的树叶的分布分别为 $\mathcal{N}(\mu_i,\Sigma_i),i=1,2,3$ ，注意，其中的 $\mu_i$ 是一个二维向量， $\Sigma_i$ 是一 $2\times2$ 的矩阵。

例如，以下Mathematica代码实现了500个示例数据的生成（三种树木的概率分别为0.2，0.3，0.5）：

generateDataCode

图1 Mathematica代码，用于生成高斯混合模型的示例数据。

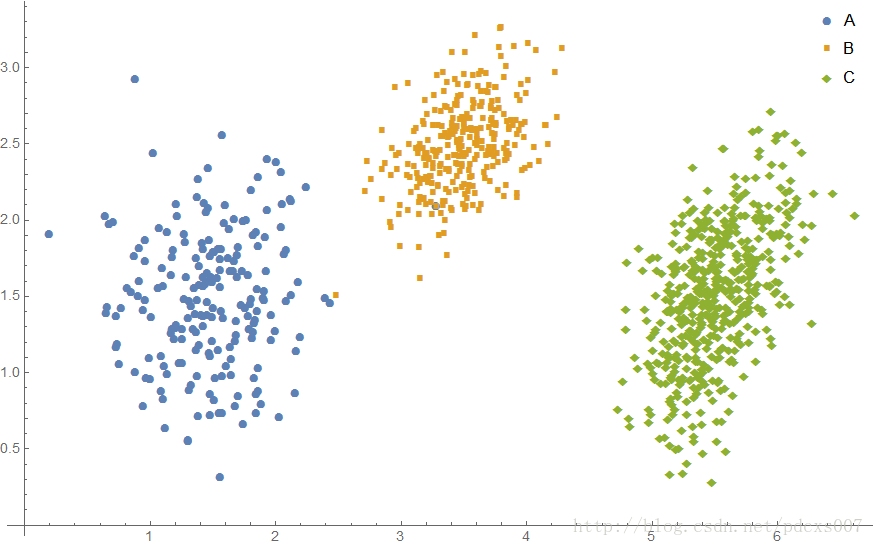
效果如图2所示：

generateData

图2 高斯混合模型示例数据

在了解了实际例子后，展示一下“官方”的高斯混合模型的定义，并指明其含混和错误的地方。

Suppose that we are given a training set $\{x^{(1)},\dots,x^{(m)}\}$ as usual. Since we are in the unsupervised learning setting, these points do net come with any labels.

We wish to model the data by specifying a joint distribution $p(x^{(i)},z^{(i)})=p(x^{(i)}|z^{(i)})p(z^{(i)})$ . Here, $z^{(i)}\thicksim \text{Multinomial}(\phi)$ , (where $\phi_j\geq 0, \sum_{j=1}^k\phi_j=1$ , and parameter $\phi_j$ gives $p(z^{(i)}=j)$ ,) and $x^{(i)}|z^{(i)}\thicksim \mathcal{N}(\mu_j,\Sigma_j)$ . We let $k$ denote the number of values that the $z^{(i)}$ ’s can take on. Thus our model posits that each $x^{(i)}$ was generated by randomly choosing $z^{(i)}$ from $\{1,\dots,k\}$ , and then $x^{(i)}$ was drawn from one of $k$ Gaussians depending on $z^{(i)}$ . This is called the mixture of Gaussians model.

大体一看会有很多难以理解的地方，这里做一下说明。首先，训练集用的是小写字体加目标的形式，不符合常理。且不加粗会误认为是标题，因此改用上文的方式，训练集记为： $\{\mathbf{x_1},\dots,\mathbf{x_m}\}$ ，第 $k$ 个训练数据的各个分量记为 $(x_1^k, x_2^k,\dots,x_c^k)$ （这里的 $c$ 表示训练数据的维数，后面并没有用到）。

“官方文档”中的 $z^{(i)}$ 和 $\mathbf{z}_i$ 是混用的。本身这两个变量是可以一一对应的，但是一个是标量一个是向量，太容易让人迷惑了，而且很多地方严格的来说是错误的。文中提到了一个多项式分布（Multinomial Distribution），这是一个怎样的分布呢？这是一个二项式分布的推广分布，对于一个实验，有 $k$ 各可能的结果，各个结果发生的可能分别为 $p_1,\dots,p_k$ ，进行了 $n$ 次独立实验之后，这 $k$ 个结果分别发生了 $a_1,\dots,a_k$ 次的概率为：

p (a 1, \dots, a k; n, p 1, \dots, p k) = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ (n a 1 , \dots , a k) p a 1 1 \dots p a k k, 0, \sum i = 1 k a i = n otherwise

$p(a_1,\dots,a_k;n,p_1,\dots,p_k)=\left\{ \begin{array}{ll} \binom{n}{a_1,\dots,a_k}p_1^{a_1}\dots p_k^{a_k}, & \sum_{i=1}^k a_i=n\\ 0, &\text{otherwise} \end{array} \right.$
式中，

(na1,…,ak)=n!a1!…ak! $\binom{n}{a_1,\dots,a_k}=\frac{n!}{a_1!\dots a_k!}$ 表示将

n $n$ 个物品分成

k $k$ 个组，每个组分别有

a1,…,ak $a_1,\dots,a_k$ 个物品的分组方式的总数目。当

k=2 $k=2$ 时，多项式分布退化为二项式分布。

由此，可以注意到，多项式分布的变量显然是一个 $k$ 维的变量，“官方文档”中说的 $z^{(i)}$ 服从多项式分布是错误的，且没有指明 $n$ 这个参数。通过开始时候举的例子，可以看到，实际上应该这样说：

$\mathbf{z}_i\thicksim \text{Multinomial}(1, \phi)$ ，其中， $\phi=(\phi_1^i,\dots,\phi_k^i)$ ，其中的 $\phi_j$ 代表 $\mathbf{x_i}$ 属于第 $j$ 类（即 $z^{(i)}=j$ ）的概率。此时，显然有 $\sum_{j=1}^k\phi_j=1$

当 $n=1$ 时，总共进行了一次实验，因此在所有的实验结果中，有且仅有一种结果出现，这才是分类想要表达的内容。

另外，对于某个具体分类的数据，都服从联合高斯分布（因为数据一般是多维的）。这就是混合高斯模型了：有若干个分类，每一类都服从联合高斯分布，每次实验数据都是这些实验的结果，服从 $n=1$ 的多项式分布。

Jensen’s Inequality

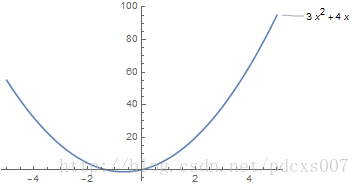
在介绍Jensen不等式之前，先要说明一下凸函数。凸函数的数学定义为，函数 $f$ 的定义域为 $\mathcal{X}$ ，若 $\mathcal{X}$ 为凸集，且有：

f (t x 1 + (1 - t) x 2) \leq t f (x 1) + (1 - t) f (x 2), \forall x 1, x 2 \in X, \forall t \in [0, 1]

$f(tx_1+(1-t)x_2)\leq tf(x_1)+(1-t)f(x_2),\forall x_1,x_2\in\mathcal{X},\forall t\in[0,1]$
注意，凸函数的图像在直观的印象中是“凹”的，如下图：

Convex Function

图3 凸函数是“凹”的。

以上式子很容易的可以推广：

f (λ 1 x 1 + λ 2 x 2 + \dots + λ n x n) = f (\sum i = 1 n λ i x i) \leq \sum i = 1 n λ i f (x i), where \sum i = 1 n λ i = 1, λ i \geq 0, i = 1, \dots, n (1)

$\tag{1} \begin{array}{c} \displaystyle f(\lambda_1x_1+\lambda_2x_2+\dots+\lambda_nx_n)=f(\sum_{i=1}^n \lambda_ix_i)\leq\sum_{i=1}^n\lambda_if(x_i), \\ \displaystyle\text{where}\quad\sum_{i=1}^n\lambda_i=1,\lambda_i\geq0,i=1,\dots,n \end{array}$
推广思路展示由2到3的推广，可以用归纳法得到一般情形。

f (λ 1 x 1 + λ 2 x 2 + λ 3 x 3) = f [λ 1 x 1 + (λ 2 + λ 3) (λ 2 λ 2 + λ 3 x 2 + λ 3 λ 2 + λ 3 x 3)] \leq λ 1 f (x 1) + (λ 2 + λ 3) f (λ 2 λ 2 + λ 3 x 2 + λ 3 λ 2 + λ 3 x 3) \leq λ 1 f (x 1) + (λ 2 + λ 3) [λ 2 λ 2 + λ 3 f (x 2) + λ 3 λ 2 + λ 3 f (x 3)] = λ 1 f (x 1) + λ 2 f (x 2) + λ 3 f (x 3)

$\begin{array}{rl} f(\lambda_1x_1+\lambda_2x_2+\lambda_3x_3)&=f\left[\lambda_1x_1+(\lambda_2+\lambda_3)\left(\frac{\lambda_2}{\lambda_2+\lambda_3}x_2+\frac{\lambda_3}{\lambda_2+\lambda_3}x_3\right)\right]\\ &\leq\lambda_1f(x_1)+(\lambda_2+\lambda_3)f\left(\frac{\lambda_2}{\lambda_2+\lambda_3}x_2+\frac{\lambda_3}{\lambda_2+\lambda_3}x_3\right)\\ &\leq\lambda_1f(x_1)+(\lambda_2+\lambda_3)\left[\frac{\lambda_2}{\lambda_2+\lambda_3}f(x_2)+\frac{\lambda_3}{\lambda_2+\lambda_3}f(x_3)\right]\\ &=\lambda_1f(x_1)+\lambda_2f(x_2)+\lambda_3f(x_3) \end{array}$
式

(1) $(1)$ 即为Jensen不等式的离散形式，可以扩展至连续形式，为：

f (\int x p (x) d x) \leq \int f (x) p (x) d x (2)

$f\left(\int xp(x)dx\right)\leq \int f(x)p(x)dx \tag{2}$

(1) $(1)$ 式和

(2) $(2)$ 式可以统一记为：

f [E (X)] \leq E [f (X)] (3)

$f[E(X)]\leq E[f(X)] \tag{3}$
注意，

X $X$ 是一个随机变量，

E(X) $E(X)$ 是

X $X$ 的期望，是一个数字，因此，

(3) $(3)$ 中的不等式左侧部分是很好理解的。比较难以理解的是

f(X) $f(X)$ ，如果对于一个随机变量取函数值，隐含的意义是将这个随机变量的所有值通过函数映射成另一个值。由此，

f(X) $f(X)$ 是一个随机变量，是点一些要注意，因此才有了对

f(X) $f(X)$ 求期望的操作。比如，如果

X $X$ 是

[0,1] $[0,1]$ 是分布的均匀分布，且

f(x)=3x2+4 $f(x)=3x^2+4$ ，则

f(X) $f(X)$ 是一个在

[4,7] $[4,7]$ 上的分布，具体概率密度可以通过概率变换公式得到，不在此处的讨论范围内。

f[E(X)]=f(0.5)=4.75 $f[E(X)]=f(0.5)=4.75$ ，

E[f(X)]=∫10(3x2+4)⋅1dx=5 $E[f(X)]=\int_0^1(3x^2+4)\cdot1dx=5$ ,可以看到此时

(3) $(3)$ 式成立。

EM算法

现在的问题是，我们抽取到一堆叶子的数据，但是不知道这些抽取到的叶子分别属于哪种树木，同时也不知道各个树木树叶的面积与最大宽度的统计规律（只知道服从什么分布，如高斯分布，但不知道该分布的具体参数）。那么可以将每个叶子自动分类，并对各种树木的叶子的分布参数作出估计吗？

乍一听是很难完成的任务，如此多的未知量，如何进行估计？EM算法便是解决这样的问题。首先，假定数据各个类别的参数都已经知道，记为 $\theta$ （一般意义上， $\theta$ 是一个向量，如在例子中的3个 $\mu$ 与3个 $\Sigma$ ）。那么给定一个 $\mathbf{x}$ ，便可以计算 $\mathbf{x}$ 发生的概率，给定一组 $\{\mathbf{x}_1,\dots,\mathbf{x}_m\}$ ，就可以计算这组采样发生的概率为：

p (x 1; θ) p (x 2; θ) \dots p (x m; θ)

$p(\mathbf{x}_1;\theta)p(\mathbf{x}_2;\theta)\cdots p(\mathbf{x}_m;\theta)$
要分析这个概率的最大值，需要进行求导操作，而多个变量连乘的导数特别复杂，因此对这个连乘进行取对数运算，将乘法变换为加法，基于这种思路定义了Likelihood函数：

l (θ) = \sum i = 1 m ln p (x i; θ)

$l(\theta)=\sum_{i=1}^m \ln p(\mathbf{x}_i;\theta)$
具体求

p(xi,θ) $p(\mathbf{x}_i,\theta)$ 时，都是利用了全概率公式，例如，在例子中，求一个采样数据出现的概率（在各个树木的高斯分布参数已知的前提下），就是分别计算如果其属于A种树木其出现的概率，如果其属于B种树木其出现的概率以及C种树木。所以，

l(θ) $l(\theta)$ 可以进一步写为：

l (θ) = \sum i = 1 m ln \sum j = 1 k p (x i, z (i) = j; θ)

$l(\theta)=\sum_{i=1}^m\ln\sum_{j=1}^k p(\mathbf{x}_i,z^{(i)}=j;\theta)$
此时，对数函数内求和又使得问题变得非常复杂，因此，利用上文提到的Jensen不等式，注意这里是凹函数，不等号方向要改变。但是还不能直接使用，需要再做如下变形：

l (θ) = \sum i = 1 m ln \sum j = 1 k p (z (i) = j) p ( x i , z ( i ) = j ; θ ) p ( z ( i ) = j ) = \sum i = 1 m ln E (p ( x i , z ( i ) ; θ ) p ( z ( i ) ))

$l(\theta)=\sum_{i=1}^m\ln\sum_{j=1}^k p(z^{(i)}=j)\frac{p(\mathbf{x}_i,z^{(i)}=j;\theta)}{p(z^{(i)}=j)}=\sum_{i=1}^m \ln E\left(\frac{p(\mathbf{x}_i,z^{(i)};\theta)}{p(z^{(i)})}\right)$
可以将

l(θ) $l(\theta)$ 放缩并简化为：

l (θ) \geq \sum i = 1 m E (ln p ( x i , z ( i ) ; θ ) p ( z ( i ) )) = \sum i = 1 m \sum j = 1 k p (z (i) = j) ln p ( x i , z ( i ) ; θ ) p ( z ( i ) ) (4)

$l(\theta)\geq \sum_{i=1}^m E\left(\ln\frac{p(\mathbf{x}_i,z^{(i)};\theta)}{p(z^{(i)})}\right)=\sum_{i=1}^m \sum_{j=1}^k p(z^{(i)}=j)\ln\frac{p(\mathbf{x}_i,z^{(i)};\theta)}{p(z^{(i)})} \tag{4}$
在上面的变换中，有一个不好理解的地方。我们将

p(xi,z(i);θ)p(z(i)) $\frac{p(\mathbf{x}_i,z^{(i)};\theta)}{p(z^{(i)})}$ 看作是随机变量

z(i) $z^{(i)}$ 的函数，以前接触的随机变量函数中，只是对随机变量的取值作变换，而在对

l(θ) $l(\theta)$ 的变换中，涉及到了随机变量在对应值处的概率。这实际上是没有问题的，概率其实可以看作是随机变量取值的一个函数，而函数的函数是复合函数，依然是一个函数，并不会对Jensen不等式产生影响。

注意，现在的假设是 $\theta$ 已知，而 $p(z^{(i)})$ 是未知的。那么很自然的就会想到，通过猜测的方式，将 $p(z^{(i)})$ 设置成合适的值，使得 $l(\theta)$ 尽可能大（也就是采样数据出现的可能性最大）。注意到 $(4)$ 式的不等号中取得等号，当且仅当随机变量可能的取值只有1个（即为常数，记为 $c$ ），则可以得到：

p ( x i , z ( i ) ; θ ) p ( z ( i ) ) = c p (z (i)) \propto p (x i, z (i); θ)

$\frac{p(\mathbf{x}_i,z^{(i)};\theta)}{p(z^{(i)})}=c\\ p(z^{(i)})\propto p(\mathbf{x}_i,z^{(i)};\theta)$
又因为

∑kj=1p(z(i)=j)=1 $\sum_{j=1}^k p(z^{(i)}=j)=1$ ，所以可以得到：

p (z (i) = j) = = = p ( x i , z ( i ) = j ; θ ) \sum k j = 1 p ( x i , z ( i ) = j ; θ ) p ( x i , z ( i ) = j ; θ ) p ( x i ; θ ) p (z (i) = j | x i; θ)

$\begin{array}{rcl} p(z^{(i)}=j) & =& \displaystyle\frac{p(\mathbf{x}_i,z^{(i)}=j;\theta)}{\sum_{j=1}^k p(\mathbf{x}_i,z^{(i)}=j;\theta)}\\ &=&\displaystyle\frac{p(\mathbf{x}_i,z^{(i)}=j;\theta)}{p(\mathbf{x}_i;\theta)}\\ &=&p(z^{(i)}=j|\mathbf{x}_i;\theta) \end{array}$
即，第

i $i$ 个观测样本属于

j $j$ 类的概率，定义为已知各个类别分布情况下(

θ $\theta$ 已知)，在

xi $\mathbf{x}_i$ 发生的前提下，该样本属于

j $j$ 类的概率。

在确定了 $p(z^{i})$ 后，可以反过来调整 $\theta$ 参数（因为这也是未知的），通过反复调整，可以逐渐得到最大的 $l(\theta)$ ，同时也就确定了各个观测值属于各个类型的概率以及各个类型分布参数的估计。

EM算法描述如下：

重复直到收敛 {

(E-Step) 对于每个观测值 $\mathbf{x}_i$ ，令

$p (z (i) = j) : = p (z (i) = j | x i; θ), j = 1, \dots, k$ $p(z^{(i)}=j):=p(z^{(i)}=j|\mathbf{x}_i;\theta),\quad j=1,\dots,k$

(M-Step) 令

$θ : = arg max θ \sum i = 1 m \sum j = 1 k p (z (i) = j) ln p ( x i , z ( i ) = j ; θ ) p ( z ( i ) = j )$ $\theta:=\arg \max_\theta \sum_{i=1}^m \sum_{j=1}^kp(z^{(i)}=j)\ln \frac{p(\mathbf{x}_i,z^{(i)}=j;\theta)}{p(z^{(i)}=j)}$

}

注意在重复开始前需要给 $\theta$ 赋一个初值。

EM算法能够保证收敛吗？假设 $\theta_t$ 和 $\theta_{t+1}$ 是两次连续的EM步骤产生的 $\theta$ 值，则可以证明 $l(\theta_t)\leq l(\theta_{t+1})$ ，又因为 $l(\theta)\leq 0$ ，所以有上界且单调递增，算法收敛。

l (θ t) = \sum i = 1 m \sum j = 1 k p t (z (i) = j) ln p ( x i , z ( i ) ; θ t ) p t ( z ( i ) = j )

$l(\theta_t)=\sum_{i=1}^m\sum_{j=1}^k p_t(z^{(i)}=j)\ln\frac{p(\mathbf{x}_i,z^{(i)};\theta_t)}{p_t(z^{(i)}=j)}$
且有：

l (θ t + 1) \geq \geq = \sum i = 1 m \sum j = 1 k p t (z (i) = j) ln p ( x i , z ( i ) ; θ t + 1 ) p t ( z ( i ) = j ) \sum i = 1 m \sum j = 1 k p t (z (i) = j) ln p ( x i , z ( i ) ; θ t ) p t ( z ( i ) = j ) l (θ t)

$\begin{array}{rcl} l(\theta_{t+1})&\geq&\displaystyle\sum_{i=1}^m\sum_{j=1}^k p_t(z^{(i)}=j)\ln\frac{p(\mathbf{x}_i,z^{(i)};\theta_{t+1})}{p_t(z^{(i)}=j)}\\ &\geq&\displaystyle \sum_{i=1}^m\sum_{j=1}^k p_t(z^{(i)}=j)\ln\frac{p(\mathbf{x}_i,z^{(i)};\theta_t)}{p_t(z^{(i)}=j)}\\ &=&l(\theta_t) \end{array}$
上式中的第一个不等式是因为E-Step对于

p(z(i)) $p(z^{(i)})$ 的最大化，第二个不等式是M-Step对于

θ $\theta$ 参数的最大化（参数最大化）。

混合高斯模型的EM算法

代入混合高斯模型后，EM算法中的计算公式都可以具体化。

E-Step是比较容易的，直接可以计算得到：

w i j = p (z (i) = j) = p ( z ( i ) = j , x i ; ϕ , μ j , Σ j ) \sum j = 1 k p ( z ( i ) = j , x i ; ϕ , μ j , Σ j )

$w_j^i=p(z^{(i)}=j)=\frac{p(z^{(i)}=j,\mathbf{x}_i;\phi,\mu_j,\Sigma_j)}{\displaystyle\sum_{j=1}^k p(z^{(i)}=j,\mathbf{x}_i;\phi,\mu_j,\Sigma_j)}$
在M-Step中，将

l(θ) $l(\theta)$ 展开，得到：

= = \sum i = 1 m \sum j = 1 k p (z (i) = j) ln p ( x i , z ( i ) = j ; ϕ , μ j , Σ j ) p ( z ( i ) = j ) \sum i = 1 m \sum j = 1 k p (z (i) = j) ln p ( x i | z ( i ) = j ; μ j , Σ j ) p ( z ( i ) = j ; ϕ ) p ( z ( i ) = j ) \sum i = 1 m \sum j = 1 k w i j ln 1 ( 2 π ) n 2 | Σ j | 1 2 exp ( - 1 2 ( x i - μ j ) T Σ - 1 j ( x i - μ j ) ) \cdot ϕ j w i j

$\begin{array}{rl} & \displaystyle\sum_{i=1}^m\sum_{j=1}^kp(z^{(i)}=j)\ln\frac{p(\mathbf{x}_i,z^{(i)}=j;\phi,\mu_j,\Sigma_j)}{p(z^{(i)}=j)}\\ =&\displaystyle\sum_{i=1}^m\sum_{j=1}^kp(z^{(i)}=j)\ln\frac{p(\mathbf{x}_i|z^{(i)}=j;\mu_j,\Sigma_j)p(z^{(i)}=j;\phi)}{p(z^{(i)}=j)}\\ =&\displaystyle\sum_{i=1}^m\sum_{j=1}^k w^i_j\ln \frac{\frac{1}{(2\pi)^{\frac n2}|\Sigma_j|^\frac12}\exp\left(-\frac12\left(\mathbf{x}_i-\mu_j\right)^T\Sigma_j^{-1}\left(\mathbf{x}_i-\mu_j\right)\right)\cdot\phi_j}{w_j^i} \end{array}$
对

μj $\mu_j$ 求偏导，可以得到：

μ j = \sum m i = 1 w i j x i \sum m i = 1 w i j

$\mu_j=\frac{\sum_{i=1}^mw^i_j \mathbf{x}_i}{\sum_{i=1}^m w^i_j}$

ϕi $\phi_i$ 仅与

wij $w^i_j$ 有关，因此仅需要求以下式子即可：

max \sum i = 1 m \sum j = 1 k w i j ln ϕ j

$\max \sum_{i=1}^m\sum_{j=1}^k w_j^i\ln\phi_j$
又疏于

∑kj=1ϕj=1 $\sum_{j=1}^k\phi_j=1$ ，所以构造拉格朗日算子，并最终得到：

ϕ j : = \sum m i = 1 w i j m

$\phi_j:=\frac{\sum_{i=1}^m w_j^i}{m}$
同理，对于

Σj $\Sigma_j$ ，有：

Σ j : = \sum m i = 1 w i j ( x i - μ j ) ( x i - μ j ) T \sum m i = 1 w i j

$\Sigma_j:=\frac{\sum_{i=1}^m w_j^i (\mathbf{x}_i-\mu_j)(\mathbf{x}_i-\mu_j)^T}{\sum_{i=1}^m w_j^i}$

实现

初始值设置为： $\phi=(0.3,0.3,0.4), \mu_1=(0,0)$ , $\mu_2=(1,0),\mu_3=(0,1)$ , $\Sigma_1=\Sigma_2=\Sigma_3=\left(\begin{matrix}1&0\\0&1\end{matrix}\right)$ .

Mathematica代码实现如下：

Source Code

源代码为：

Clear["`*"];
m = 1000;
\[Mu] = {{1.5, 1.5}, {3.5, 2.5}, {5.5, 1.5}};
\[Sigma] = {({
     {0.2, 0},
     {0, 0.2}
    }), ({
     {0.1, 0.05},
     {0.05, 0.1}
    }), ({
     {0.1, 0.08},
     {0.08, 0.2}
    })};
z = Table[t = RandomReal[]; Which[t < 0.2, 1, t < 0.5, 2, True, 3], m];
x = Table[
   RandomVariate[
    MultinormalDistribution[\[Mu][[z[[i]]]], \[Sigma][[z[[i]]]]]], {i,
     m}];
ListPlot[{Pick[x, z, 1], Pick[x, z, 2], Pick[x, z, 3]},
 PlotLegends -> Placed[{"A", "B", "C"}, {Right, Top}], 
 PlotMarkers -> Automatic]
guessPhi = {0.3, 0.3, 0.4};
guessMu = {{0, 0}, {1, 0}, {0, 1}};
guessSigma = {({
     {1, 0},
     {0, 1}
    }), ({
     {1, 0},
     {0, 1}
    }), ({
     {1, 0},
     {0, 1}
    })};
t = 1;
While[True,
  w = Table[Table[N@
       guessPhi[[j]] PDF[
        MultinormalDistribution[guessMu[[j]], guessSigma[[j]]], 
        x[[i]]]/Sum[
        guessPhi[[j]] PDF[
          MultinormalDistribution[guessMu[[j]], guessSigma[[j]]], 
          x[[i]]], {j, 1, 3}], {j, 1, 3}], {i, 1, m}];
  updateGuessMu = 
   Table[Sum[w[[i, j]] x[[i]], {i, 1, m}], {j, 1, 3}]/Total[w];
  updateGuessPhi = Total[w]/m;
  updateGuessSigma = 
   Table[Sum[
     w[[i, j]] Outer[Times, x[[i]] - updateGuessMu[[j]], 
        x[[i]] - updateGuessMu[[j]]]/Total[w[[All, j]]], {i, 1, 
      m}], {j, 1, 3}];
  (*Print[t,updateGuessMu,updateGuessPhi,updateGuessSigma];*)
  If[Fold[And, Thread[Flatten[updateGuessMu - guessMu] < 0.001]] && 
    Fold[And, Thread[Flatten[updateGuessPhi - guessPhi] < 0.001]] && 
    Fold[And, 
     Thread[Flatten[updateGuessSigma - guessSigma] < 0.001]], Break[]];
   guessMu = updateGuessMu;
  guessPhi = updateGuessPhi;
  guessSigma = updateGuessSigma;
  t = t + 1;
  ];
guessZ = Flatten@Table[Position[w[[i]], Max[w[[i]]]], {i, m}];
ListPlot[{Pick[x, guessZ, 1], Pick[x, guessZ, 2], Pick[x, guessZ, 3]},
  PlotLegends -> 
  Placed[{"Auto Class A", "Auto Class B", "Auto Class C"}, {Right, 
    Top}], PlotMarkers -> Automatic]
updateGuessMu
updateGuessPhi
Map[MatrixForm, updateGuessSigma, 1]

原始数据图像：

Original Data

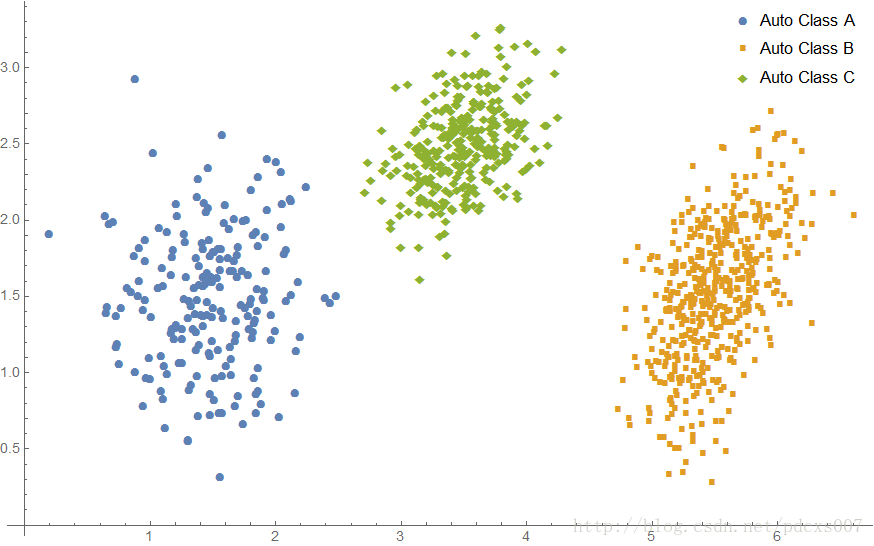
学习到的分类图像：

Guess Data

学习到的参数及原参数的对比：

Guess Data

注意，由于算法自动分类，类型B和类型C是反着的，不过不影响算法的使用。

以上就是EM算法与高斯混合模型的笔记啦。