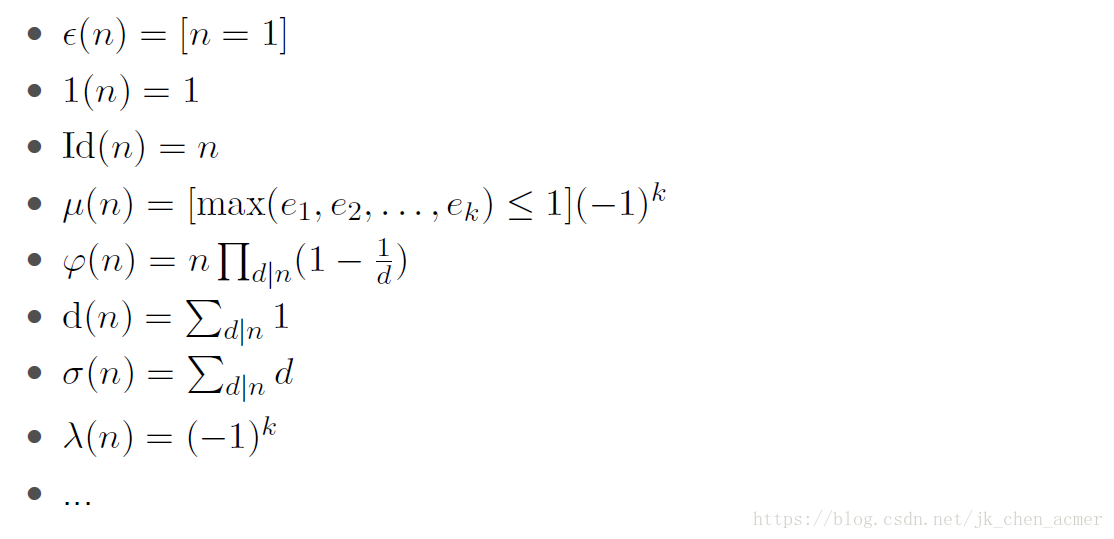杜教筛（下）：狄利克雷卷积

定义：

定义$f,g$两个积性函数的狄利克雷卷积运算(*)为：

$$(f*g)(n)=\sum_{d|n}f(d)*g(\frac{n}{d})$$

性质：

狄利克雷卷积满足：

1. 交换律：$f*g=g*f$
2. 结合律：$(f*g)*h=f*(g*h)$
3. 分配律：$f*(g+h)=f*h+g*h$
4. 单位元：$f*e=f$

常见函数卷积：

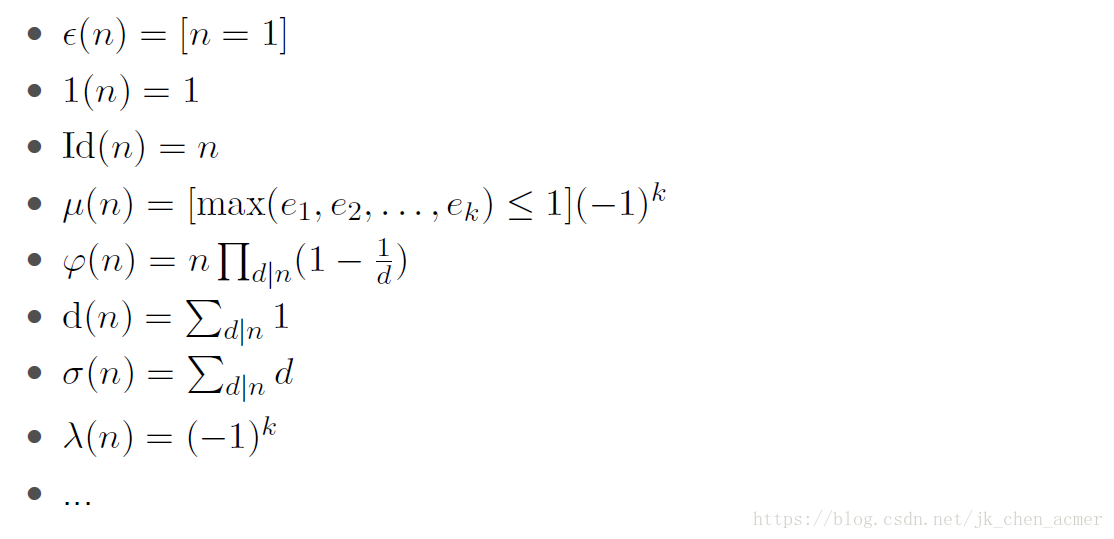
$μ∗1=ϵ$ (莫比乌斯函数与1互为逆元)
$ϕ∗1=Id$ (欧拉函数与n互为逆元)
$ϕ=Id∗μ$ (莫比乌斯与欧拉的关系)

$d=1∗1$
$1=μ∗d$

$\\$

---

$\\$

杜教筛：

由于涉及内容太多，分成两篇博客进行讲述，建议先看前一篇，就当你已经看完前一篇了，我这里会讲的快一点

求$\sum_{i=1}^nf(i)$，设为$Ans(n)$

找一个积性函数g(x)，那么

$$\sum_{i=1}^{n}(f*g)(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)*f(\frac{n}{d})$$ 前一篇中有理论证明，这里对出数学证明，显然： $$\sum_{i=1}^{n}\sum_{d|i}=\sum_{d=1}^{n}\sum_{d|i}^{i<=n}$$ 那么： $$\sum_{i=1}^{n}(f*g)(i)=\sum_{d=1}^{n}\sum_{d|i}^{i<=n}g(d)*f(\frac{n}{d})=\sum_{d=1}^{n}g(d)\sum_{j=1}^{[\frac{n}{d}]}f(j)$$ 接下来和前一篇一样： $$\because\sum_{d=1}^{n}g(d)\sum_{j=1}^{[\frac{n}{d}]}f(j)=\sum_{d=2}^{n}g(d)\sum_{j=1}^{[\frac{n}{d}]}f(j)+g(1)\sum_{j=1}^{n}f(j)\\\therefore g(1)*Ans(n)=\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)Ans(n/d)$$ 结论： $$Ans(n)=\dfrac{\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)Ans(n/d)}{g(1)}$$

按照上一篇的说法，递归+整除分块+线性筛 收尾。

$\\$

---

$\\$

例题：

求$\sum_{i=1}^n\phi(i)*i$

显然，如果卷一个函数1的话，变成$\sum_{i=1}^n\sum_{d|i}\phi(d)*d$，好像并没有什么简单的化简，而卷一个函数$Id$的话，就变成了

$$\sum_{i=1}^n\sum_{d|i}\phi(d)*d*\frac{i}{d}\to\sum_{i=1}^ni\sum_{d|i}\phi(d)$$ 而 $\sum_{d|i}\phi(d)=i$，所以得到： $$令：f(i)=\phi(i)*i\;,\;g(i)=i\;,\;Ans(n)=\sum_{i=1}^n\phi(i)*i\\得：Ans(n)=\dfrac{\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)Ans(n/d)}{g(1)}\\=\sum_{i=1}^{n}i^2-\sum_{d=2}^{n}d*Ans(n/d)$$ 这题就变得异常简单了

总结：

当求积性函数前缀和不好求的时候，用狄利克雷卷上一个积性函数，使卷完后的式子的前缀和变得简单，卷完后的前缀和算出来基本上题目就完成了

• 如果出现$\phi(x)$，那么就凑$\sum_{d|n}\phi(d)=n$
• 如果是$u(x)$，就凑$\sum_{d|n}^{n\not=1}u(d)=0$