牛客练习赛27 F 计数（状态压缩dp + 矩阵快速幂优化）

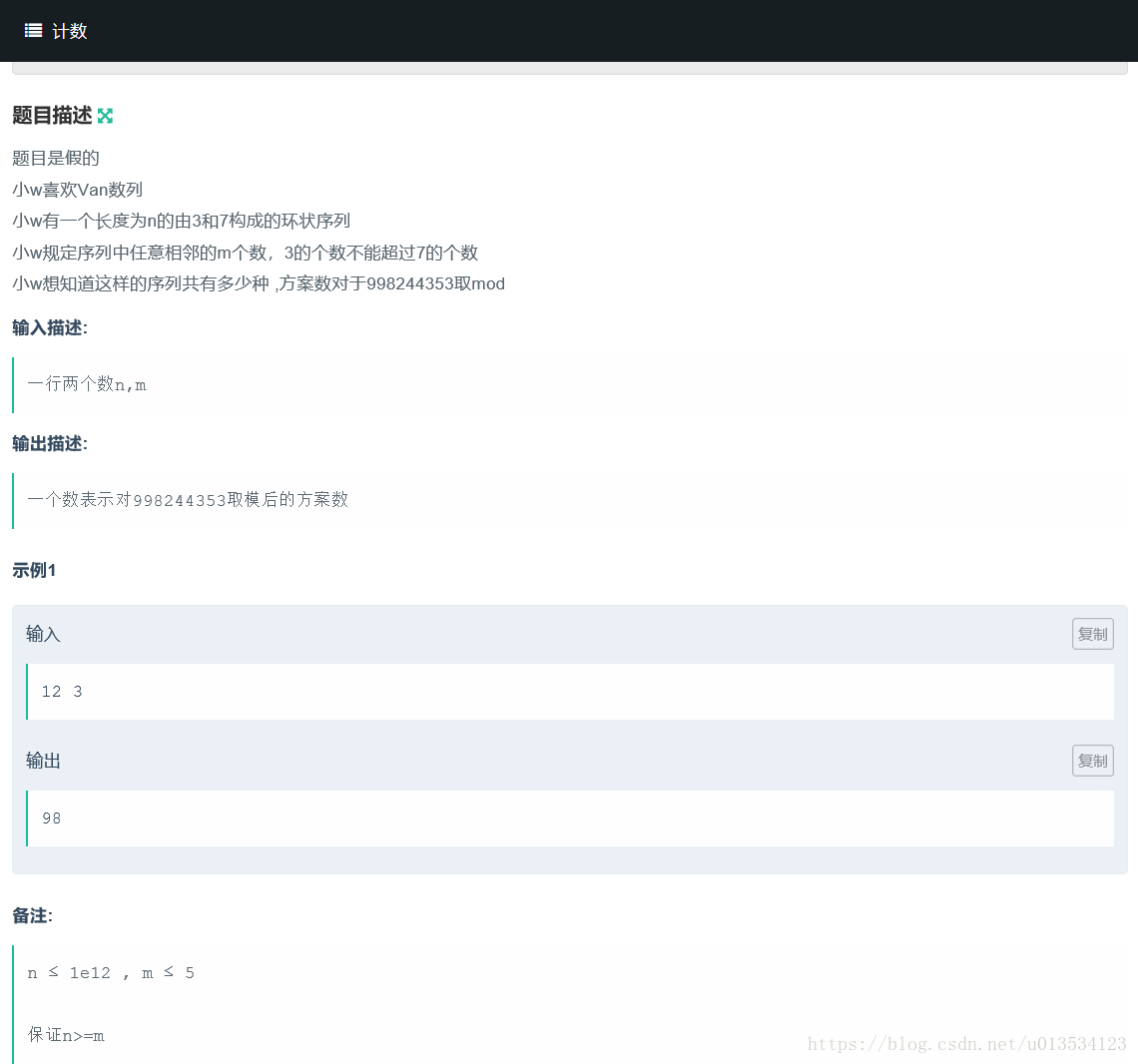
中文题。

由于m最大范围只有5，而且每一个位置只能够填写3和7，所以我们不妨考虑状压，用0和1分别表示3和7，这样就是一个5位的二进制数字。那么我们的限制条件也可以很好的通过位运算来判断。接着我们考虑这么多个位置如何计算方案数。首先，我们简化问题，把问题变成一条链而不是一个圈，这样一个位置可以放什么数字就只是与前面四个位置有关系。如果之前的7的个数已经大于3的个数，那么当前位置放3和7都可以，否则就只能够放7。这样我们就可以写出状态转移方程：

$\small dp[i][status]=dp[i-1][status>>1]+dp[i-1][status>>1|(1<<(m-1)]$

其中dp[i][status]表示处理到第i个格子，当前状态位status的时候的方案数。显然当前状态根据往前第m个数字的状态，可以有最多两种选择。status>>1表示往前第m个数字取0的方案，status>>1|(1<<(m-1))表示往前第m个数字取1的方案。注意到这个转移方程，dp[i]只与dp[i-1]相关，又这个长度最多可以到1e12这么大，所以我们可以想到用矩阵快速幂去优化这个转移。转移矩阵也是很好构建，对于每一个状态，最多可以从之前的两个状态转移过来，类似于转移方程那样构造转移矩阵即可。

现在，我们结合这题要求是换状来考虑这个问题。既然是换状，把变成链状来处理求出来之后，必然会有些方案是不合法的。引因为链状只是考虑了前四个，而环状之后最后m个位置还要往后考虑。于是我们不妨枚举一下最初m个位置的状态，然后再对应的枚举一下最后m个位置的状态，根据两个状态来判定这种组合是否合法。如果合法，那么把这一种组合方式的方案数加上。对于一个特定的起始状态x和最最终状态y，如果他们匹配合法，那么相当于是在初始的时候，只有x这个状态为1，最后的时候只有y这个状态为1，所以对应的方案数就是转移矩阵的(n-m)次方的第x行第y列的数值。把所有合法的起始状态和最终状态对应转移矩阵的(m-n)次方的对应位置的值求和就是最后的答案。具体见代码：

#include<bits/stdc++.h>
#define mod 998244353
#define LL long long
#define pb push_back
#define lb lower_bound
#define ub upper_bound
#define INF 0x3f3f3f3f
#define sf(x) scanf("%lld",&x)
#define sc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define clr(x,n) memset(x,0,sizeof(x[0])*(n+5))
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;
 
const int N = 32;
 
LL n,m,up;
 
struct Matrix
{
    LL a[N][N];
    Matrix(){memset(this,0,sizeof(Matrix));}
 
    Matrix operator *(const Matrix x) const
    {
        Matrix ans;
        for(int i=0;i<up;i++)
            for(int j=0;j<up;j++)
            {
                for(int k=0;k<up;k++)
                    ans.a[i][j]+=a[i][k]*x.a[k][j]%mod;
                ans.a[i][j]%=mod;
            }
        return ans;
    }
 
    friend Matrix operator ^(Matrix x,LL y)
    {
        Matrix ans;
        for(int i=0;i<up;i++)
            ans.a[i][i]=1;
        while(y)
        {
            if (y&1) ans=ans*x;
            x=x*x; y>>=1;
        }
        return ans;
    }
} x;
 
inline bool check(int x)
{
    assert(x<up);
    return __builtin_popcount(x)>=(m+1)/2;
}
 
void init()
{
    for(int i=0;i<up;i++)
    {
        if (!check(i)) continue;
        int j=i>>1;
        if (check(j)) x.a[i][j]=1;
        j|=up>>1;
        if (check(j)) x.a[i][j]=1;
    }
}
 
int main()
{
    LL ans=0;
    sf(n); sf(m);
    up=(1<<m); init();
    x=x^(n-m);
    for(int i=0;i<up;i++)
    {
        if (!check(i)) continue;
        for(int j=0;j<up;j++)
        {
            if (!check(j)) continue;
            int tmp=(j<<m)|i,flag=0;
            for(int k=1,s=up-1;k<m;k++)
                if (!check((tmp&(s<<k))>>k)) {flag=1;break;}
            if (!flag)
                ans=(ans+x.a[j][i])%mod;
        }
    }
    printf("%lld\n",(ans+mod)%mod);
    return 0;
}

牛客练习赛27 F 计数（状态压缩dp + 矩阵快速幂优化）

猜你喜欢