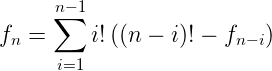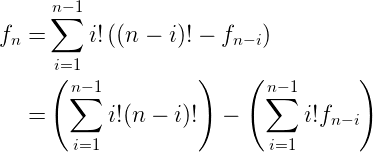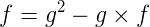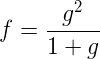牛客练习赛32 F Friendly Polynomial（NTT + 多项式逆元 + 组合计数）

大致题意：一个数列，如果存在一个i∈[1,n-1]，使得前i个数字是1-i的一个排列，那么这个数列和不合法的。现在问1-n的排列中，有多少个不合法的数列。

首先，我们定义一个不合法的序列，它仅被最大的一个i给计算，也即前i个数字是排列，后i+1~n个数字不是排列的情况。这个时候，我们令fn表示长度为n的不合法数列个数，那么显然有：

$\large f_n=\sum_{i=1}^{n-1}i!\left((n-i)!-f_{n-i}\right)$

表示，长度为n的不合法数列个数，首先是前i个要是一个排列，那么有i!种方式。然后后面一定不存在一个排列，那么后面的方案数就是总方案书减去有排列的个数。那么现在考虑如何计算这个数字。

$\large \begin{aligned} f_n =&\sum_{i=1}^{n-1}i!\left((n-i)!-f_{n-i}\right) \\ =&\left(\sum_{i=1}^{n-1}i!(n-i)!\right)-\left(\sum_{i=1}^{n-1}i!f_{n-i}\right) \\ \end{aligned}$

变成下面以后，我么可以分为前后两个部分，前后两部分都是NTT的形式。我们令0!=0，gn为n!的函数。那么就变成了： $\large f=g^2-g \times f$

整理一下可以有：

$\large f=\frac{g^2}{1+g}$

那么，我们需要的fn只需要对右边的式子求一个多项式逆元即可。具体见代码（偷了HNU emofunx的板子，实在是太全了）

#include <bits/stdc++.h>
#define LL long long
using namespace std;

const int mod = 998244353;//(119 << 23) + 1;
const int modinv2 = (mod+1)/2; // 1/2 in F_p
const int G = 3;
const int N = 540010;
const int maxn = 530000;

int f[N],g[N],fac[N];

//取模加减乘
inline int add(int a,int b) {return a+b>=mod?a+b-mod:a+b;}
inline void inc(int&a,int b) {if ((a+=b)>=mod) a-=mod;}
inline int sub(int a,int b) {return a-b<0?a-b+mod:a-b;}
inline void dec(int&a,int b) {if ((a-=b)<0) a+=mod;}
inline int mul(int a,int b) {return (LL)a*b%mod;}
inline int qpow(int x,int n) {int ans=1;for (;n;n>>=1,x=(LL)x*x%mod) if (n&1) ans=(LL)ans*x%mod; return ans;}//quick power
//-------------------------------NTT--------------------------------
int wn[30],iwn[30]; //wn[i] = G^((P-1)/(2^i)) (mod P), iwn[i] = wn[i]^(-1) (mod P)
inline void init() //do this before NTT
{
    wn[23] = qpow(G,(mod-1)/(1<<23));
    for (int i=22;i>=0;i--) wn[i] = mul(wn[i+1],wn[i+1]);
    iwn[23] = qpow(wn[23],(1<<23)-1);
    for (int i=22;i>=0;i--) iwn[i] = mul(iwn[i+1],iwn[i+1]);
}
inline void revbin_permute(int a[],int n) {
    int i=1, j=n>>1, k;
    for (;i<n-1;i++) {
        if (i < j) swap(a[i],a[j]);
        for (k=n>>1;j>=k;) {j -= k; k >>= 1;}
        if (j < k) j += k;
    }
}
void NTT(int f[],int ldn,int is) {
    int n = (1<<ldn);
    revbin_permute(f,n);
    for (int i=0;i<n;i+=2) {
        int tmp1 = f[i], tmp2 = f[i+1];
        f[i] = add(tmp1,tmp2), f[i+1] = sub(tmp1,tmp2);
    }
    for (int ldm=2;ldm<=ldn;ldm++) {
        int m = (1<<ldm), mh = (m>>1);
        int dw = is>0?wn[ldm]:iwn[ldm], w = 1;
        for (int j=0;j<mh;j++) {
            for (int r=0;r<n;r+=m) {
                int u = f[r+j], v = mul(f[r+j+mh],w);
                f[r+j] = add(u,v);
                f[r+j+mh] = sub(u,v);
            }
            w = mul(w,dw);
        }
    }
}
//多项式乘法
void convolution(int f[],int g[],int n) {
    int ldn; for (int i=20;i>=0;i--) if (n&(1<<i)) {ldn=i;break;}
    NTT(f,ldn,1); NTT(g,ldn,1); //会改变g
    for (int i=0;i<n;i++) f[i] = mul(f[i],g[i]);
    NTT(f,ldn,-1);
    int iv = qpow(n,mod-2);
    for (int i=0;i<n;i++) f[i] = mul(f[i],iv);
}

//多项式求sq
void polysq(int f[],int n) {
    int ldn; for (int i=20;i>=0;i--) if (n&(1<<i)) {ldn=i;break;}
    NTT(f,ldn,1);
    for (int i=0;i<n;i++) f[i] = mul(f[i],f[i]);
    NTT(f,ldn,-1);
    int iv = qpow(n,mod-2);
    for (int i=0;i<n;i++) f[i] = mul(f[i],iv);
}

//多项式求inv
//Q(2n) = Q(n) - P*Q^2(n)
void polyinv(int f[],int n) {
    static int g[maxn],b[maxn],c[maxn];
    for (int i=0;i<n;i++) g[i]=0;
    g[0] = qpow(f[0],mod-2);
    for (int i=2;i<=n;i<<=1) {
        for (int j=0;j<i;j++) b[j] = g[j], c[j] = f[j];
        for (int j=i;j<2*i;j++) b[j] = c[j] = 0;
        polysq(b,2*i);
        for (int j=i;j<2*i;j++) b[j] = 0;
        convolution(b,c,2*i);
        for (int j=0;j<i;j++) g[j] = (2ll*g[j] - b[j] + mod)%mod;
    }
    for (int i=0;i<n;i++) f[i] = g[i];
}

int main()
{
    init(); int T;
    scanf("%d",&T); g[1]=f[1]=1;
    for(int i=2;i<=100000;i++)
        g[i]=f[i]=(LL)f[i-1]*i%mod;
    int lg; for(lg=1;lg<=100000;lg<<=1);
    polysq(g,lg<<1); f[0]++;
    polyinv(f,lg<<1);
    convolution(f,g,lg<<2);
    while(T--)
    {
        int x;
        scanf("%d",&x);
        printf("%d\n",f[x]);
    }
    return 0;
}

牛客练习赛32 F Friendly Polynomial（NTT + 多项式逆元 + 组合计数）

猜你喜欢