1.线性回归
1.1模型
1.1.1目标函数(损失函数、正则)
a.无正则:最小二乘线性回归(OLS)
b.L2正则:岭回归(Ridge Regression)
c.L1正则:Lasso
1.1.2概率解释
最小二乘线性回归等价于极大似然估计
Recall:极大似然估计
线性回归的MLE
正则回归等价于贝叶斯估计
小结:目标函数
1.2优化求解
1.2.1 OLS的优化求解(解析解)
1.2.2 OLS的优化求解(梯度下降)
梯度下降
OLS的梯度下降
1.2.3 OLS的优化求解(随机梯度下降,SGD)
1.2.4 岭回归的优化求解
1.2.5 Lasso的优化求解——坐标下降法
坐标下降法
小结:线性回归之优化求解
1.3模型评估与模型选择
1.3.1 评价准则
1.3.2 Scikit learn中回归评价指标
1.3.3 线性回归中模型选择
1.3.4 RidgeCV
1.3.5 LassoCV
小结:线性回归之模型选择
1.1模型
机器学习是根据训练数据对变量之间的关系进行建模。当输出变量(响应变量)y∈R是连续值时,我们称之为回归分析,即用函数描述一个或多个预测变量与响应变量y之间的关系,并根据该模型预测新的观测值对应的响应。
①给定训练数据,其中y∈R是连续值,一共有N个样本,回归分析的目标是学习一个输入X到输出y的映射f
②对新的测试数据x,用学习到的映射f对其进行预测:
③若假设映射f是一个线性函数,即
称之为线性回归模型
1.1.1目标函数(损失函数、正则)
机器学习模型的目标函数包含两项:损失函数L和正则项R,分别代表度量模型与训练数据
的匹配程度(损失函数越小越匹配)和对模型复杂度的“惩罚”以避免过拟合。
因此目标函数最小要求和训练数据拟合得好,同时模型尽可能简单。体现了机器学习的基本准则:奥卡姆剃刀定律(Occam's Razor),即简单有效原则。
对回归问题,损失函数可以采用L2损失(可以根据实际情况选择其他有意义的损失函数),得到
即残差的平方。对线性回归,所有样本的残差平方和为残差平方和(RSS):
a.无正则:最小二乘线性回归(OLS)
由于线性模型比较简单,实际应用中有时正则项为空,得到最小二乘线性回归(OLS)(此时目标函数中只有残差平方和,“平方”的古时候的称为“二乘”),即
b.L2正则:岭回归(Ridge Regression)
正则项可以为L2正则,得到岭回归(Ridge Regression)模型:
c.L1正则:Lasso
正则项也可以选L1正则,得到Lasso模型:
①当λ取合适值,Lasso(least absolute shrinkage and selection operator)的结果是稀疏的(w的某些元素系数为0,起到特征选择作用
1.1.2概率解释
a.最小二乘线性回归等价于极大似然估计
①假设:
②其中为线性预测和真值之间的残差
③我们通常假设残差的分布为 , 均值为0,方差为
。对该残差分布的基础上,加上y的分布,因此线性回归可以写成:
其中。均值移动变化,方差没有变。
注意:由于假设残差为0均值的正态分布,最小二乘线性回归的残差
b.Recall:极大似然估计
极大似然估计(MLE)定义为(即给定参数的情况下,数据D出现的概率为p,则MLE取使得p最大的参数
)
其中(log)似然函数为
① 表示在参数为的情况下,数据
出现的概率
② 极大似然:选择数据出现概率最大的参数
c.线性回归的MLE
①OLS的似然函数为
②极大似然可等价地写成极小负log似然损失(NLL)(在sklearn中,叫做logloss)
在上式中,观察第二项即可得知OLS的RSS项与MLE是等价的关系(相差常数倍不影响目标函数取极值的位置)
d.正则回归等价于贝叶斯估计
①假设残差的分布为,线性回归可写成:
②若假设参数w中每一维的先验分布为,并假设w中每一维独立,则
分布的均值为0,即我们偏向于较小的系数值,从而得到的曲线也比较平滑;
其中,控制先验的强度
③根据贝叶斯公式,参数的最大后验估计(MAP)为
等价于最小目标函数
④对比岭回归的目标函数(L2正则)
⑤L1正则等价于先验为Laplace分布,即
小结:目标函数
①线性回归模型也可以放到机器学习一般框架:损失函数+正则
损失函数:L2损失
正则:无正则、L2正则、L1正则、L2+L1正则
②正则回归模型可视为先验为正则、似然为高斯分布的贝叶斯估计
L2正则:先验分布为高斯分布
L1正则:先验分布为Laplace分布
1.2优化求解
线性回归的目标函数
①无正则的最小二乘线性回归(OLS)
② L2正则的岭回归(Rideg Regression)模型:
③L1正则的Lasso模型
模型训练
模型训练是根据训练数据求解最优模型参数,即求目标函数取极小值的参数
根据模型的特点和问题复杂程度(数据、模型),可选择不同的优化算法
一阶的导数为0:
二阶导数>0:
1.2.1 OLS的优化求解(解析解)
将OLS的目标函数写成矩阵形式(省略因子1/N,不影响目标函数取极小值的位置)
只取与w有关的项,得到
求导:
recall:向量求导公式:(w为y,A为,
为对称矩阵,
):
所以,得到
实际应用中通常通过对输入X进行奇异值分解(SVD),求解更有效
对X进行奇异值分解:
则
所以
1.2.2 OLS的优化求解(梯度下降)
a.梯度下降
在求解机器学习算法的模型参数(无约束优化问题)时,梯度下降是最常用的方法之一。梯度下降法是一个一阶最优化算法,通常也称为最速下降法。
一元函数f(x)在x处的梯度为函数f在点x处的导数。对多元函数在点
处,共有D个偏导数,分别是f在该点关于
的偏导数,...,以及关于
的偏导数,将这D个偏导数组合成一个D维矢量,称为函数f在x处的梯度。梯度一般记为
或grad,即
函数f在某点梯度指向在该点函数值增长最快的方向。因此要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度的反方向(负梯度方向)进行迭代搜索。梯度下降法的每一步通常会这么写
其中为学习率(步长)
梯度下降的基本步骤:
1)确定学习率,并初始化参数
2)计算目标函数在当前参数值
的梯度:
3)梯度下降更新参数:
4)重复以上步骤,直到收敛(目标函数的下降量小于某个阈值),得到目标函数的局部极小值以及最佳参数值
b.OLS的梯度下降
OLS的目标函数为:
梯度为:
参数更新公式为:
或者卸除标量形式为:
1.2.3 OLS的优化求解(随机梯度下降,SGD)
① 在上述梯度下降算法中,梯度
利用所有的样本,因此被称为“批处理梯度下降”
② 随机梯度下降:每次只用一个样本
优点:
通常收敛会更快,且不太容易陷入局部极值
亦被称为在线学习
对大样本数据集尤其有效
③ SGD的变形
可以用于离线学习:每次看一个样本,对所有样本可重复多次循环使用(一次循环称为一个epoch)
每次可以不止看一个样本,而是看一些样本
1.2.4 岭回归的优化求解
岭回归的目标函数与OLS只相差一个正则项(w的二次函数),所以类似可得:
求导,得到
计算时也可以采用对X进行SVD得到:
注:岭回归的优化实现代码很容易从OLS的优化推导
1.2.5 Lasso的优化求解——坐标下降法
①坐标下降法
坐标下降法,是沿着坐标轴的方向去下降。为了找到一个函数的局部极小值,坐标轴下降法在每次迭代中可以在当前点处沿一个坐标方向进行一维搜索。在整个过程中循环使用不同的坐标方向。一个周期的一维搜索迭代过程相当于一个梯度迭代。而梯度下降是根据目标函数的导数(梯度)来确定搜索方向,沿着梯度的负方向下降。该梯度方向可能不与任何坐标轴平行。不过梯度下降和坐标轴下降的共性都是迭代法,通过启发式的方式一步步迭代求解函数的最小值,坐标下降法在稀疏矩阵上的计算速度非常快,同时也是Lasso回归最快的解法。
坐标轴下降法的数学依据主要是如下结论:一个可微的凸函数,其中
是D维向量,即有D个维度。如果在某一点
,使得
在每一个坐标轴
,上都是最小值,那么
就是一个全局的最小值。于是我们的优化目标就是在
的D个坐标轴上(或者说向量的方向上)对损失函数作迭代的下降,当所有的坐标轴上的
都达到收敛时,我们的损失函数最小,此时的
即为我们要求的结果
算法过程如下:
1)初始化为一随机初值。记为
,上标括号中的数字表示迭代次数;
2)对第t轮迭代,我们依次计算:
也就是说是使
最小化的
的值。此时
中只有
是变量,其余均为常量,因此最小值容易通过求导求得。
3)检查向量和
向量在各个维度上的变化情况,如果在所有维度上变化都足够小,那么
即为最终结果,否则转入第2步,继续第t+1轮的迭代。
② Lasso的优化求解推荐采用坐标下降法
但项在
处不可微(不平滑优化问题)
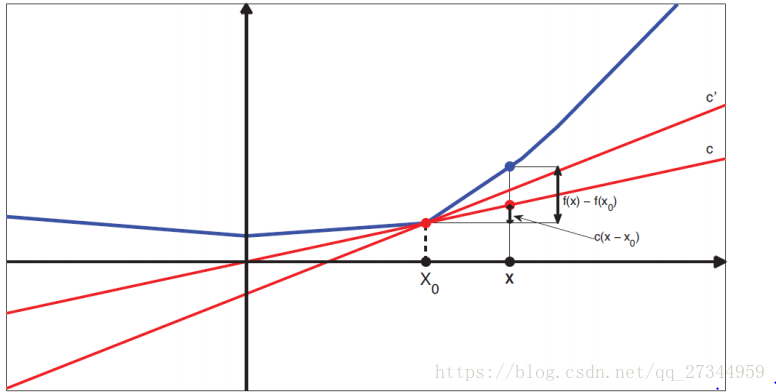
为了处理不平滑函数,扩展导数的表示,定义一个(凸)函数f在点的次梯度或者次导数为一个标量g,使得
其中I为包含的某个区间
定义区间[a,b]的子梯度集合为
所有次梯度的区间被称为函数f在的次微分,用
小结:线性回归之优化求解
1.3模型评估与模型选择
1.3.1 评价准则
1.3.2 Scikit learn中回归评价指标
1.3.3 线性回归中模型选择
1.3.4 RidgeCV
1.3.5 LassoCV
小结:线性回归之模型选择