最小二乘法—牛顿法

文章目录

最小二乘法
二、牛顿法（Newton’s method）

牛顿法和梯度下降法的效率对比：
牛顿法的优缺点总结：

三、拟牛顿法

最小二乘法

二、牛顿法（Newton’s method）

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f(x)=0的根。牛顿法最大的特点就在于它的收敛速度很快。

具体步骤：: 首先，选择一个接近函数 $f(x)$ 零点的 $x_0$ (起始位置)，计算相应的 $f(x_0)$ 和切线斜率 $f′(x_0)$ 。
然后我们计算穿过点$(x_0,f(x_0)) $并且斜率为$ f′(x_0)$的直线和 $x$ 轴的交点的x坐标，也就是求如下方程的解：
$x·f'(x_0)+f(x_0)-x_0·f'(x_0)=0$; 我们将新求得的点的 $x$ 坐标命名为 $x_1$ ，通常 $x_1$ 会比 $x_0$ 更接近方程 $f(x)=0$ 的解。
因此我们现在可以利用 $x1$ 开始下一轮迭代。迭代公式可化简为如下所示：
$x_{n+1} = x_n -\frac{f(x_n)}{f'(x_n)}$

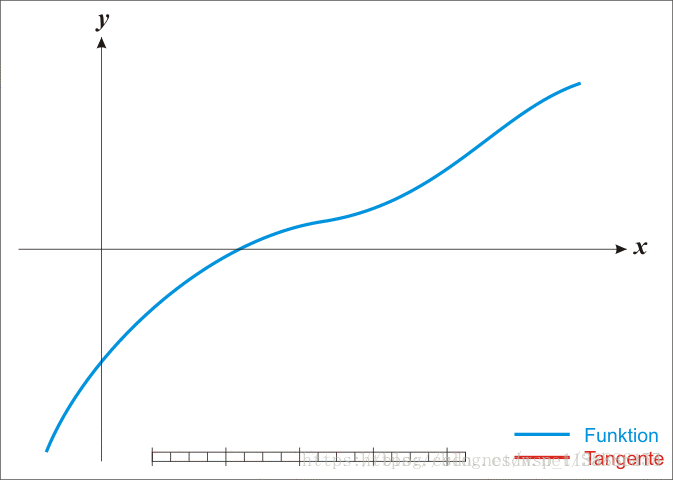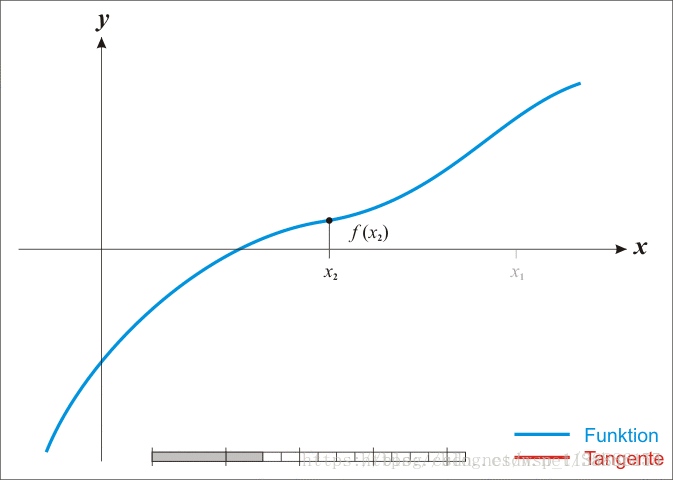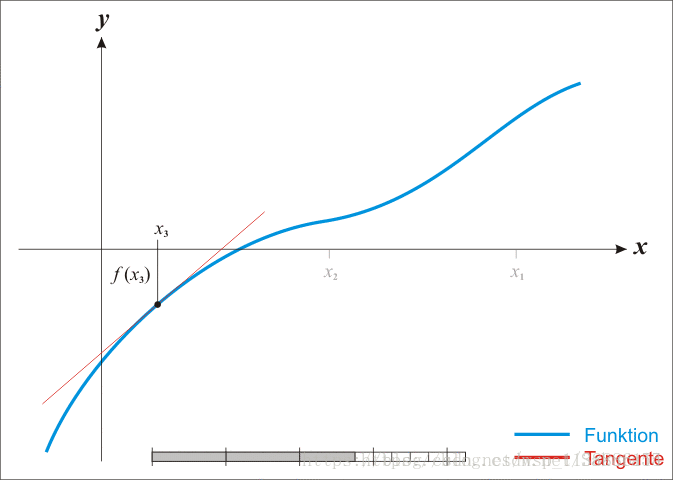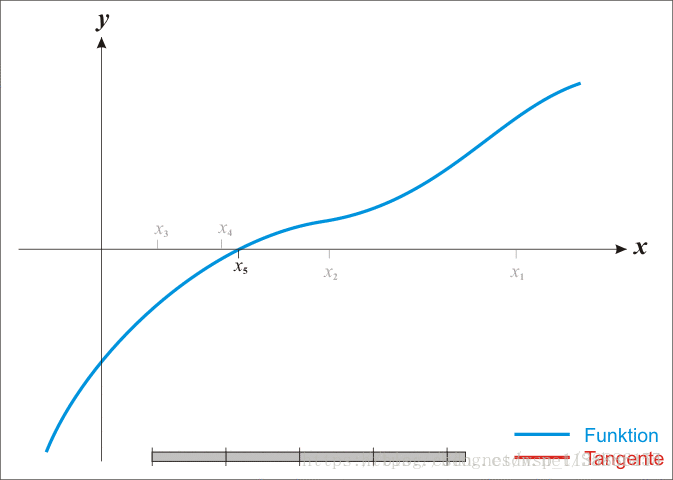
已经证明，如果f′是连续的，并且待求的零点x是孤立的，那么在零点x周围存在一个区域，只要初始值x0位于这个邻近区域内，那么牛顿法必定收敛。并且，如果f′(x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。
这里写图片描述

牛顿法和梯度下降法的效率对比：

从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。
通俗地说，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，
牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。
所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。
（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

牛顿法的优缺点总结：

优点：二阶收敛，收敛速度快；
　　缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。

三、拟牛顿法

拟牛顿法是求解非线性优化问题最有效的方法之一。: 拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。
拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。
通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这
类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟 牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。
如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。