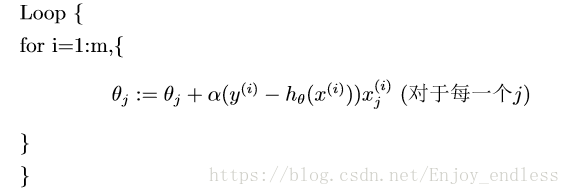首先最小二乘法是用来干什么的,他的目的是最小化误差平方之和,从而找到最优训练模型,这个模型可以用来更好的拟合训练的样本数据。
最小二乘法具体包括的执行算法有:随机梯度下降和牛顿法;随机梯度下降很简单,具体介绍在上一篇博客(与批梯度下降对比)及之前博客已有介绍;在这里重点学习一下牛顿法。
**
一、随机梯度下降:
再放一张随机梯度下降法的求解过程,以用来最后于牛顿法做一些对比:
二、牛顿法:
牛顿法的核心思想利用的是:泰勒展开!
(其实泰勒展开式仅是另一种表达等式方式而已,没必要深究,其实原理也很简单不在赘述)
泰勒展开式:
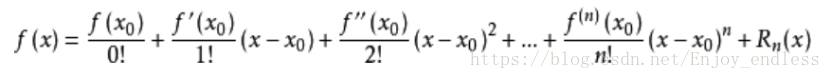
1、Guass-Newton:一阶泰勒展开求零点

在这里主要看的是解X k+1与X k的关系表示;
2、最优化求解(最小二乘法:Newton):二阶泰勒展开求最优点

其实如上图片已经解释的很详细了,二阶泰勒展开后对其求最优值(在模型当中最优值就是平方差和最小的值),如何求一个函数的最优值那就是求导为0的点,也就是对上面min函数内部求导使其值为0即式6如上,最后同样求出了X k+1与X k的关系;
最后并给出了利用牛顿法求解最优问题的迭代统一形式;
3、了解了牛顿法之后,现在我们将其应用于模型当中的具体实践中:
首先单个样本损失函数表示如下、并对其求一、二阶导:
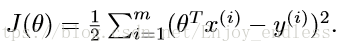
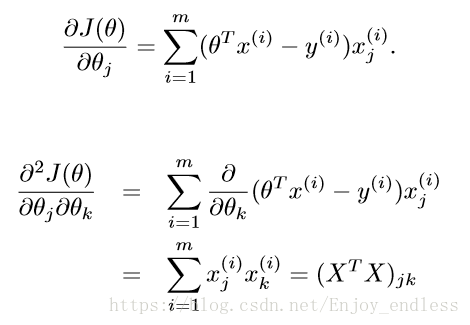
这里注意一点,前面的求和式转变成了后面的表达式是:矩阵乘法的转换(矩阵!!)
然后我们这里有了有了一阶导数、二阶导数,对比牛顿法我们可以写出此时的参数1与参数0之间的关系如下:
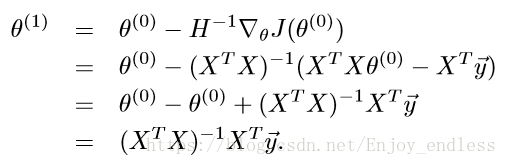
在这里的H就是二阶导数的简化表示,后面的J()就是对参数一阶求导数的表示;注意这里的参数及大写的X与y都是表示的矩阵(所有样本系数、未知数x及值yi共同组成的矩阵!其中二阶导数矩阵H就是hessian矩阵)
到这里牛顿法应用于求解模型最优解参数就算是介绍完了(注意:模型优化的过程就是一步步的更新参数,上面已经表示出了后一个参数与前一个参数的关系式)
三、对比随机梯度下降与牛顿法:
其实看其两式之间的差异已经非常明显了,一个是循环迭代(随机梯度下降法)求最后值,一个是一步出结果(牛顿法);是不是感觉有些不可思议,其实仔细一想、一看两者的区别也没有那么明显了;
为什么牛顿法可以一步出结果,因为他一步就把所有的xi、yi及参数全部以矩阵的形式计算进去了!所有这么来看两者也没有什么区别可言了!
但是在真正执行的工程当中,矩阵乘是有其独特优势的,因为大部分框架都已经将矩阵乘计算进行了封装优化(如python中numpy到pytorch中的Variable等等),不论是看起来还是操作起来都是十分方便快捷的!