简单介绍

sklearn中的LinearRegression类拟合了一个带有系数 $\theta=(\theta_1,\theta_2,...,\theta_n)$ 的线性模型，使得数据集实际观测数据和预测数据之间的残差平方和最小：

m i n_{θ} | | X θ - y | |_{2}^{2}

$min_{\theta}||X \theta-y||^2_2$

其中向量 $\theta=(\theta_1,\theta_2,...,\theta_n)$ 为coef_，定义 $\theta_0$ 为intercept_

coef为系数、intercept为截距；
sklearn在coef和intercept后加上的下划线是为了表明这个是模型更新的属性。

数学解释

普通最小二乘法是解决线性回归问题最为普通的一种方法。

约定:
- $x^{(i)}$ 表示第 $i$ 个样本点
- $x_j^{(i)}$ 表示第 $i$ 个样本点的第 $j$ 个特征
- $x_j$ 表示样本点 $x$ 的第 $j$ 个特征

$n$ 维平面里有 $m$ 个点 $x_1, x_2, x_3, ..., x_m$ , 其中 $x_i = ((x_{i, 1}, x_{i, 2}, ...x_{i, n}), y_i)$

假设函数 $hypothesis$ :

\hat{y} = h_{θ} (x) = θ_{0} + θ_{1} x_{1} + θ_{2} x_{2} + . . . + θ_{n} x_{n}

$\hat y=h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n$

h y p o t h e s i s

$hypothesis$ 的向量形式:

y = X θ

$y=X\theta$
其中:

y = {[\begin{matrix} y^{(1)} y^{(2)} \dots y^{(m)} \end{matrix}]}_{m \times 1} X = {[\begin{matrix} 1 & x_{1}^{(1)} & x_{2}^{(1)} & . . . & x_{n}^{(1)} \\ 1 & x_{1}^{(2)} & x_{2}^{(2)} & . . . & x_{n}^{(2)} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & x_{1}^{(m)} & x_{2}^{(m)} & ⋮ & x_{n}^{(m)} \end{matrix}]}_{m \times (n + 1)} θ = {[\begin{matrix} θ_{0} \\ θ_{1} \\ . . . \\ θ_{n} \end{matrix}]}_{(n + 1) \times 1}

$y=\begin{bmatrix} y^{(1)}y^{(2)}…y^{(m)} \end{bmatrix}_{m×1} X=\begin{bmatrix}1&x^{(1)}_1&x^{(1)}_2&...&x^{(1)}_n\\ 1&x^{(2)}_1&x^{(2)}_2&...&x^{(2)}_n\\ \vdots &\vdots &\vdots &\ddots&\vdots\\ 1&x^{(m)}_1&x^{(m)}_2&\vdots&x^{(m)}_n\end{bmatrix}_{m×(n+1)} \theta=\begin{bmatrix}\theta_0\\\theta_1\\...\\\theta_n\end{bmatrix}_{(n+1)×1}$

点 $s_i$ 的残差:

a x_{i} + b - y_{i}

$ax_i+b - y_i$

损失函数(残差平方和):

J (θ) = \frac{1}{2 m} \sum_{i = 1}^{m} (h_{θ} (x^{(i)}) - y^{(i)})^{2}

$J(\theta)=\frac 1 {2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$

损失函数的向量形式:

J (θ) = \frac{1}{2 m} (X θ - y)^{T} (X θ - y)

$J(\theta)=\frac 1 {2m}(X\theta-y)^T(X\theta-y)$

最小二乘法推导过程:

由 $\frac {\partial J(\theta)} {\partial \theta}=0$ 得出：

         $\frac 1 {2m}2X^T(X\theta-y)=0$
         $X^T(X\theta-y)=0$
         $X^TX\theta-X^Ty=0$
         $X^TX\theta=X^Ty$
         $(X^TX)^{-1}X^TX\theta=(X^TX)^{-1}X^Ty$
         $\theta=(X^TX)^{-1}X^Ty$

使用矩阵求解回归系数的方法不需要对数据进行归一化处理, 而用梯度下降法则需要
当维度未上万, 用最小二乘法, 维度上万了, 用梯度下降法

对于普通最小二乘的系数估计问题，其依赖于模型各项的相互独立性。当各项是相关的，且设计矩阵 X 的各列近似线性相关，那么，设计矩阵会趋向于奇异矩阵，这会导致最小二乘估计对于随机误差非常敏感，产生很大的方差。例如，在没有实验设计的情况下收集到的数据，这种多重共线性（multicollinearity）的情况可能真的会出现。

sklearn中的最小二乘

1、首先从sklearn的linear_model(即线性模型)模块中引用LinearRegression类并实例化一个对象(该对象即为一个模型)。该类实现了普通最小二乘法。

from sklearn.linear_model import LinearRegression
model = LinearRegression()

该方法使用 $X$ 的奇异值分解来计算最小二乘解。如果 $X$ 是一个 size 为 $(n, p)$ 的矩阵，设 $n \geq p$ ，则该方法的复杂度为 $O(n p^2)$

LinearRegression类有4个参数：

参数	解释	默认值	说明
fit_intercept	是否为该模型计算截距	True	如果设为False，计算的时候将不会考虑截距(如当你的数据已经中心化了可以设为False，否则不是特殊情况不建议修改改参数)。
normalize	是否在训练之前对X做归一化处理	False	如果设置为False，训练之前可以使用`sklearn.preprocessing.StandardScaler`来做归一化处理；如果设置为True，X将减去平均值然后除以 $l_2$ 范数
copy_X	是否保存一个X的副本	True	如果为True，保存一个副本，否则会被重写
n_jobs	计算机并行数	1	如果设为-1，所有cpu均会启用。只有当标签数大于1或者处理大型数据时这个选项才会起作用，一般情况不建议修改。

看到这么多参数讲真有点头疼，庆幸的是LinearRegression将这几个参数都设置了默认值，而且sklearn会尽量保证所设置的默认值最合理最高效(特别是在一些带超参数的模型如svm中，这点尤为重要)

2、然后使用model的fit方法来训练该模型

X = [[0, 0], [1, 1], [2, 2]]  # features
y = [0, 1, 2] # labels
model.fit(X, y)  # 训练

fit方法有3个参数

参数	解释	默认值	说明
X	训练数据	无	[n_samples, n_features]形状的numpy数组或稀疏矩阵。如果是别的形式(如列表)，将被自动转成numpy数组
y	目标值	无	[n_samples, n_targets]形状的numpy数组。如果是一维的，会自动转成[n_samples, 1]的形状
sample_weight	样本的权重	None	[n_samples]形状的numpy数组，是否计算样本的权重，若为None，则所有样本权重相等

3、调用model的属性来查看训练结果

print(model.coef_)
print(model.intercept_)

运行结果为

[0.5, 0.5]
2.220446049250313e-16

我们看到截距项约为 $2.2*10^{-16}$ ，近乎为0。其实手动计算一下我们会发现截距项就是0，之所以会出现intercept_非常接近于0但不为0这种情况，是因为计算机计算误差，不能保证完全一样。当然这个误差可以忽略不计。

4、利用predict方法进行预测

X2 = [[3, 4], [5, 6]]
print(model.predict(X2))

运行结果为

[3.5, 5.5]

predict方法只有X这一个参数

参数	解释	默认值	说明
X	需要预测的样本	无	[n_samples, n_features]形状的numpy数组

5、利用score方法计算 $R^2$ 系数

关于 $R^2$ 系数的数学解释，请查看这里

X_test = [[1.5, 2.5], [3.5, 4.5]]
y_test = [2.1, 3.9]
print(model.score(X_test, y_test))

运行结果为

0.9876543209876545

这个结果可以说是相当高了，说明数据拟合得非常好。

score方法有三个参数

参数	解释	默认值	说明
X	测试样本	无	[n_samples, n_features]
y	X的真实值	无	[n_samples]或[n_samples, n_outputs]
sample_weight	样本权重	None	[n_samples]

sklearn的api设计得十分合理，这5个方法在别的大部分算法里也可以套用，这一点对新人还是很友好的。

举个栗子

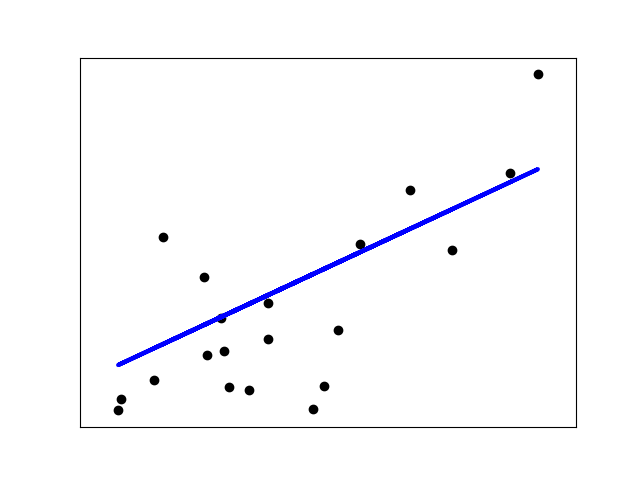
此示例使用糖尿病数据集的第一个特征。在图中可以看到直线，显示线性回归如何尝试绘制直线，这将最好地最小化残差平方。然后还计算了模型的系数，残差平方和 $R^2$ 系数。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

# 读取糖尿病数据
diabetes = datasets.load_diabetes()


# 仅使用一个特征
diabetes_X = diabetes.data[:, np.newaxis, 2]

# 将features分为训练集和测试集
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# 将labels分为训练集和测试集
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

# 创建线性回归模型对象
regr = linear_model.LinearRegression()

# 训练
regr.fit(diabetes_X_train, diabetes_y_train)

# 预测
diabetes_y_pred = regr.predict(diabetes_X_test)

# 模型的系数
print('Coefficients: \n', regr.coef_)
# 均方误差
print("Mean squared error: %.2f"
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# R^2系数
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))

# 绘图
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()

运行结果为

Coefficients:
 [ 938.23786125]
Mean squared error: 2548.07
Variance score: 0.47

普通最小二乘法

简单介绍

数学解释

sklearn中的最小二乘

举个栗子

猜你喜欢