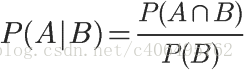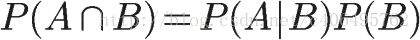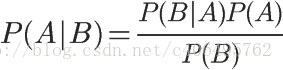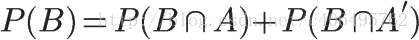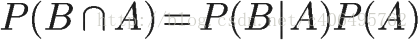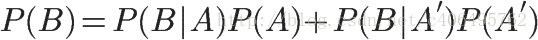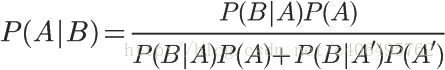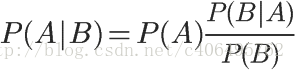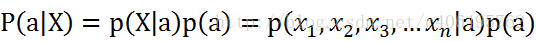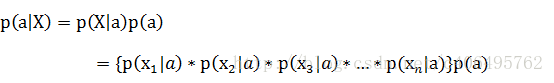一.概念:
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。首先学习贝叶斯理论。
二.贝叶斯理论 :
1 贝叶斯决策理论
假设现在我们有一个数据集,它由两类数据组成,数据分布如下图所示:
我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中红色圆点表示的类别)的概率,用p2(x,y)表示数据点(x,y)属于类别2(图中蓝色三角形表示的类别)的概率,那么对于一个新数据点(x,y),可以用下面的规则来判断它的类别:
- 如果p1(x,y) > p2(x,y),那么类别为1
- 如果p1(x,y) < p2(x,y),那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。已经了解了贝叶斯决策理论的核心思想,那么接下来,就是学习如何计算p1和p2概率。
2 条件概率
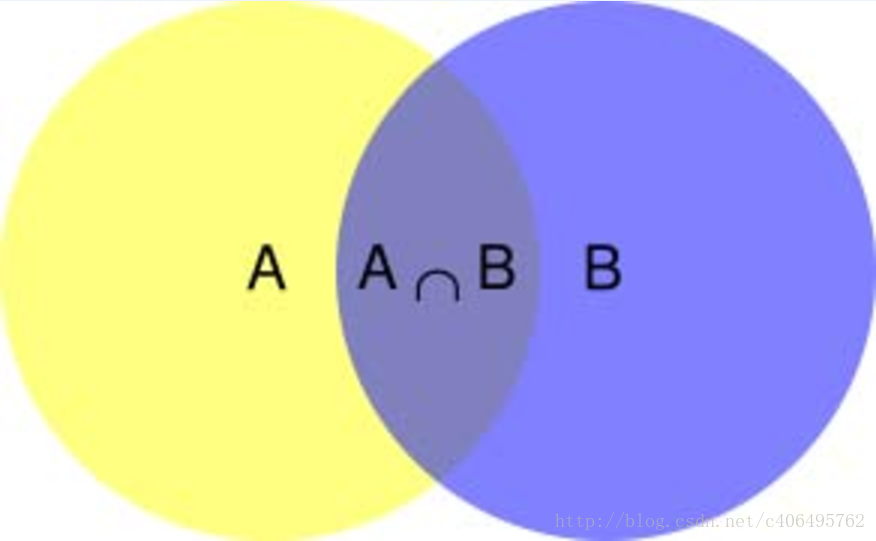
在学习计算p1和p2概率之前,我们需要了解什么是条件概率(Condittional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
因此,
同理可得,
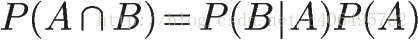
所以,
即
这就是条件概率的计算公式。
3 全概率公式
除了条件概率以外,在计算p1和p2的时候,还要用到全概率公式,因此,这里继续推导全概率公式。
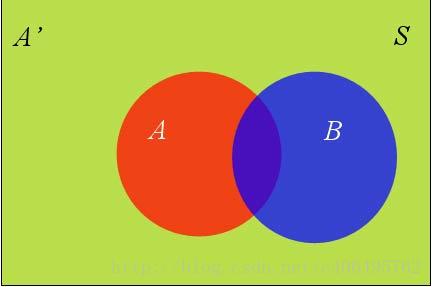
假定样本空间S,是两个事件A与A’的和。
上图中,红色部分是事件A,绿色部分是事件A’,它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。
即
在上一节的推导当中,我们已知
所以,
这就是全概率公式。它的含义是,如果A和A’构成样本空间的一个划分,那么事件B的概率,就等于A和A’的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法:
4 贝叶斯推断
对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为”先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子- 这就是贝叶斯推断的含义。我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是削弱了”先验概率”,由此得到更接近事实的”后验概率”。
在这里,如果”可能性函数”P(B|A)/P(B)>1,意味着”先验概率”被增强,事件A的发生的可能性变大;如果”可能性函数”=1,意味着B事件无助于判断事件A的可能性;如果”可能性函数”<1,意味着”先验概率”被削弱,事件A的可能性变小。
5 朴素贝叶斯推断
理解了贝叶斯推断,那么让我们继续看看朴素贝叶斯。贝叶斯和朴素贝叶斯的概念是不同的,区别就在于“朴素”二字,朴素贝叶斯对条件个概率分布做了条件独立性的假设。 比如下面的公式,假设有n个特征:
由于每个特征都是独立的,我们可以进一步拆分公式
这样我们就可以进行计算了。如果有些迷糊,让我们从一个例子开始讲起,你会看到贝叶斯分类器很好懂,一点都不难。
6 极大似然估计
模型推导
极大似然估计法认为参数是固有的,但是可能由于一些外界噪声的干扰,使数据看起来不是完全由参数决定的。没关系,数学家们觉得,虽然有误差存在,但只要让在这个数据给定的情况下,找到一个概率最大的参数就可以了。那问题其实就变成了一个条件概率最大的求解,即求使得p(θ|D)p(θ|D) 最大的参数θθ,形式化表达为求解
argmaxθp(θ|D)
而根据条件概率公式有
因为我们在极大似然估计中假设 θθ 是确定的,所以p(θ)p(θ)就是一个常数。p(D)p(D) 同样是根据已有的数据得到的,也是确定的,或者我们可以把其看作是对整个概率的一个归一化因子。这时候,求解公式(1)(1) 就变成了求解
的问题。
(3)式中的p(D|θ)p(D|θ) 就是似然函数,我们要做的就是求一个是似然最大的参数,所以称为极大似然估计。
想求解这个问题,需要假设我们的数据是相互独立的。D={x1,x2,x3,...,xn}D={x1,x2,x3,...,xn},这时候有
一般对(4)式取对数求解对数极大似然,就可以把连乘变成求和,然后求导取极值点就是要求的参数值,不在此赘述。
实例
为了便于理解,我们以之前的抛硬币实验作为实例。
回到当时我们一开始抛硬币实验,D=(1,1,0)D=(1,1,0) , θ=ρθ=ρ 的话,我们可以得到
然后使用对数极大似然估计就可以得到参数ρ 的值了。
7 可能的问题以及改进
A.贝叶斯估计
https://blog.csdn.net/liu1194397014/article/details/52766760
用极大似然估计可能出现所要估计的概率为0的情况, 这样会影响到计算后验概率的结果。采用贝叶斯估计,条件概率的贝叶斯估计是:
其中懒么大(>=0)。当=1时,称为拉普拉斯平滑。
B.解决下溢出:
另外一个遇到的问题就是下溢出,这是由于太多很小的数相乘造成的。学过数学的人都知道,两个小数相乘,越乘越小,这样就造成了下溢出。在程序中,在相应小数位置进行四舍五入,计算结果可能就变成0了。为了解决这个问题,对乘积结果取自然对数。通过求对数可以避免下溢出或者浮点数舍入导致的错误。同时,采用自然对数进行处理不会有任何损失。
三 总结
朴素贝叶斯推断的一些优点:
- 生成式模型,通过计算概率来进行分类,可以用来处理多分类问题。
- 对小规模的数据表现很好,适合多分类任务,适合增量式训练,算法也比较简单。
朴素贝叶斯推断的一些缺点:
- 对输入数据的表达形式很敏感。
- 由于朴素贝叶斯的“朴素”特点,所以会带来一些准确率上的损失。
- 需要计算先验概率,分类决策存在错误率。
参考资料:
- Jack-cui https://blog.csdn.net/c406495762/article/details/77341116
- 李航《统计学》