0. 前言

数据的特征数量，又称作向量的维度。降维（dimensionality reduction）是通过一些方法，减少数据的特征数量，以降低维度，通常采用主成分分析PCA（Principal Component Analysis）。降维的作用有：

数据压缩，减小占用的存储空间
加快算法的计算速度
低维平面可以可视化数据

初始作如下定义：

$x_{j}^{(i)}$ --- 第 $i$ 个数据的第 $j$ 个向量
$x$ --- 向量
$x_{approx}$ --- 高维向量映射到低维平面后，在高维空间中的位置
$z$ --- 高维向量映射到低维平面后，在低维空间中的位置

1. 主成分分析（PCA）

主成分分析PCA是寻找一个低维平面，使得各个数据点到平面的投影距离最小，换句话说，就是寻找 $k$ 个向量，作为子空间，将数据映射到这个子空间上，则数据的维度转换为 $k$ 。

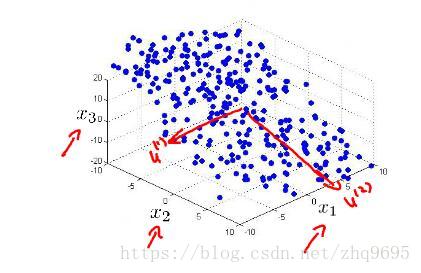
如下图所示（图源：吴恩达机器学习），三维空间的数据几乎可看作分布在一个斜面上，则可在这个斜面上建立一个二维的平面，将数据映射上去，转换为二维空间。

2. 主成分分析PCA的流程

主成分分析PCA的流程主要由两部分组成：

数据预处理（均值归一化）
计算低维空间向量（计算协方差 $\rightarrow$ 奇异值分解 $\rightarrow$ 计算低维矩阵 $\rightarrow$ 转换为低维数据）

数据预处理主要是进行均值归一化，对每个特征值进行如下变化：

$\large \begin{align*} \mu_{j} &=\frac{1}{m}\sum_{i=1}^{m}x_{j}^{(i)} \\ x_{j}^{(i)} &:= \frac{x_{j}^{(i)}-\mu_{j}}{s_{j}} \end{align*}$

均值归一化可使得特征的均值为 $0$ ，其中 $s_{j}$ 为特征缩放（取值范围的最大值减去最小值，使之取值范围接近 $[-1,1]$ ）。

计算低维空间向量，首先计算数据的协方差矩阵，采用如下公式，注意 $(x^{(i)})(x^{(i)})^{T}$ 是一个矩阵：

$\large \Xi =\frac{1}{m}\sum_{i=1}^{m}(x^{(i)})(x^{(i)})^{T}$

进行奇异值分解，在matlab中，可有如下公式：

$\large [U,S,V]=svd(\Xi)$

其中 $U$ 是一个 $n*n$ 的矩阵， $U=\begin{bmatrix} ... & &... \\ u^{(1)} &... &u^{(n)} \\ ... & & ... \end{bmatrix}$ ，取前 $k$ 列，得到 $U_{reduce}=\begin{bmatrix} ... & &... \\ u^{(1)} &... &u^{(k)} \\ ... & & ... \end{bmatrix}$ ，为一个 $n*k$ 的矩阵，接着：

$\large z=(U_{reduce})^{T}\cdot x$

将每一个向量 $x$ 转换为 $z$ ， $z$ 为 $k*1$ 的向量，达到了降维的目的。

注：最后一步转换的 $x$ 是没有偏置 $x_{0}$ 的。

3. 低维空间维度的选择

我们已知主成分分析是要寻找一个低维平面，使得各个数据点到这个平面的距离最小，这个距离可采用平均投影误差的平方（average squared projection error）量化，定义如下：

$\large \frac{1}{m}\sum_{i=1}^{m}\left\|x^{(i)}-x_{approx}^{(i)}\right\|^{2}$

其中， $x_{approx}$ 是在高维空间中映射到低维平面上的近似点（维度仍然是高维，与 $z$ 不同， $z$ 的维度是低维）， $x_{approx}=U_{reduce}\cdot z$ 。

我们需寻找满足下式的最小的 $k$ ：

$\large \frac{\frac{1}{m}\sum_{i=1}^{m}\left\|x^{(i)}-x_{approx}^{(i)}\right\|^{2}} {\frac{1}{m}\sum_{i=1}^{m}\left\|x^{(i)}\right\|^{2}}\leqslant 0.01$

其中，右侧的数值可根据实际情况调整， $0.01$ 为保证了 $99\%$ 的方差。

此外，还有一种计算方法，在奇异值分解 $[U,S,V]=svd(\Xi)$ 中， $S=\begin{bmatrix} s_{11} & &0 \\ & ... & \\ 0 & &s_{nn} \end{bmatrix}$ ，满足下式：

$\large \frac{\frac{1}{m}\sum_{i=1}^{m}\left\|x^{(i)}-x_{approx}^{(i)}\right\|^{2}} {\frac{1}{m}\sum_{i=1}^{m}\left\|x^{(i)}\right\|^{2}}= 1-\frac{\sum_{i=1}^{k}s_{ii}}{\sum_{i=1}^{n}s_{ii}}$

只需求解最小的 $k$ ，满足下式即可：

$\large 1-\frac{\sum_{i=1}^{k}s_{ii}}{\sum_{i=1}^{n}s_{ii}}\leqslant 0.01$

4. 主成分分析使用方式

用主成分分析PCA防止过拟合是不适合的，过拟合应该采用正则化
在项目中，应首先试着不采用PCA，若达不到预想的想过，则可采用PCA试试看

如果这篇文章对你有一点小小的帮助，请给个关注喔~我会非常开心的~

吴恩达机器学习（十二）主成分分析（降维、PCA）

目录

0. 前言

1. 主成分分析（PCA）

2. 主成分分析PCA的流程

3. 低维空间维度的选择

4. 主成分分析使用方式

猜你喜欢