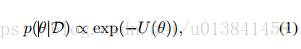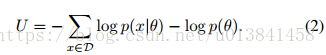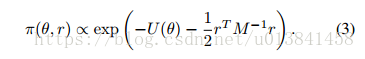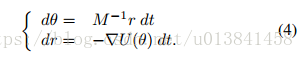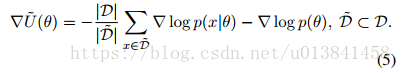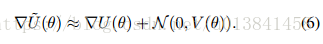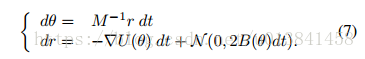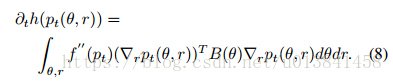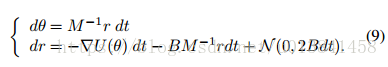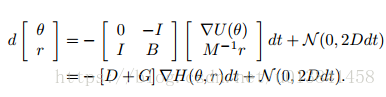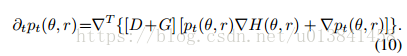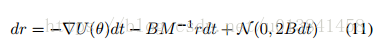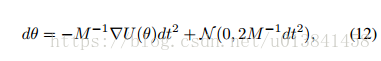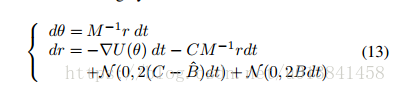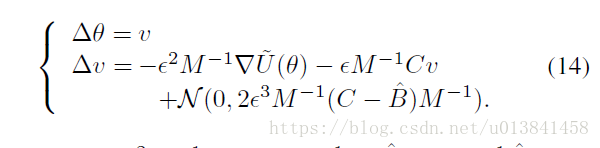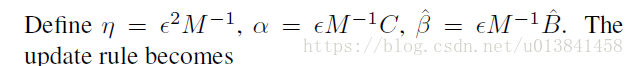Abstract
哈密尔顿蒙特卡罗(HMC)抽样方法提供了一种机制,用于在Metropolis-Hastings框架中定义具有高接受概率的远程建议,从而比标准随机游走建议更有效地探索状态空间。近年来,这种方法的普及已经显着增长。然而,HMC方法的限制是用于模拟哈密顿动力系统所需的梯度计算 - 这种计算在涉及大样本大小或流数据的问题中是不可行的。相反,我们必须依赖于从数据子集计算的噪声梯度估计。在本文中,我们探讨了这种随机梯度HMC方法的性质。令人惊讶的是,随机近似的自然实现可能是任意不好的。为了解决这个问题,我们引入了一个使用二阶Langevin动力学的变体,其摩擦项抵消了噪声梯度的影响,将所需的目标分布保持为不变分布。模拟数据的结果验证了我们的理论。我们还提供了我们的方法应用于使用神经网络的分类任务和在线贝叶斯矩阵分解。
1. Introduction
Hamiltonian Monte Carlo(HMC)(Duane等,1987; Neal,2010)采样方法提供了强大的马尔可夫链蒙特卡罗(MCMC)采样算法。 这些方法根据我们期望样本的目标分布定义哈密顿函数 - 势能 - 以及由一组“动量”辅助变量参数化的动能项。 基于对动量变量的简单更新,可以从哈密尔顿动力系统模拟,该系统能够实现远距离状态的建议。 目标分布在这些动态下是不变的; 在实践中,需要连续时间系统的离散化,需要Metropolis-Hastings(MH)校正,尽管仍具有高接受概率。 基于HMC在快速探索状态空间方面的吸引力特性,HMC方法最近越来越受欢迎(Neal,2010; Hoffman&Gelman,2011; Wang等,2013)。
然而,HMC的限制是必须计算势能函数的梯度以模拟哈密顿动力系统。我们越来越多地面对具有数百万到数十亿观察的数据集,或者数据作为流进入的数据集,我们需要在线推断,例如在线广告或推荐系统。在这些越来越常见的大批量或流数据场景中,这种梯度计算是不可行的,因为它们利用整个数据集,因此不适用于“大数据”问题。最近,在各种机器学习算法中,我们目睹了利用基于数据小批量的梯度的噪声估计来扩展算法的许多成功(Robbins&Monro,1951; Hoffman等,2013; Welling& Teh,2011)。这些发展中的大部分都是基于优化的算法(Robbins&Monro,1951; Nemirovski等,2009),并且问题在于是否可以通过基于采样的算法获得类似的效率,该算法为贝叶斯保持了许多理想的理论属性。推理。在采样环境中应用此类方法的一种尝试是最近提出的随机梯度Langevin动力学(SGLD)(Welling&Teh,2011; Ahn等人,2012; Patterson&Teh,2013)。该方法建立在一阶Langevin动力学的基础上,该动力学不包括HMC的关键动量项。
在本文中,我们探讨了将HMC的状态空间探索效率与随机梯度的大数据计算效率相结合的可能性。这样的算法将使得能够快速探索后验的大规模和在线贝叶斯采样算法成为可能。作为第一次切割,我们考虑简单地对HMC应用随机梯度修改并评估噪声梯度的影响。我们证明了由随机梯度在系统中注入的噪声不再导致哈密顿动力学,其具有期望的目标分布作为平稳分布。因此,即使在离散化动力系统之前,我们也需要纠正这种影响。可以通过MH步骤校正注入的梯度噪声,尽管这本身需要对整个数据集进行昂贵的计算。实际上,人们可能会建议在MH校正之前进行长时间的模拟运行,但由于哈密顿量与注入噪声的偏差很大,这会导致接收率低。使用最近的结果(Korattikara等,2014; Bardenet等,2014)可以潜在地改善该MH步骤的效率。在本文中,我们引入了随机梯度HMC方法,其中摩擦力增加了动量更新。我们假设注入的噪声是高斯的,吸引中心极限定理,并分析相应的动力学。我们表明使用这种二阶Langevin动力学使我们能够将所需的目标分布维持为静止分布。也就是说,摩擦抵消了注入噪声的影响。对于离散化系统,我们考虑让步长趋于零,这样就不需要MH步长,从而为我们提供了显着的计算优势。根据经验,我们证明即使设置为小的固定值,我们也有良好的性能。补充材料中提供了这种小方法的理论计算与准确性权衡。
许多模拟实验验证了我们的理论结果,并证明了(i)精确HMC,(ii)随机梯度HMC的简单实现(简单地用随机梯度代替梯度)和(iii)我们提出的方法之间的差异。 结合摩擦力。 我们还比较了SGLD的一阶Langevin动态。 最后,我们将所提出的方法应用于使用贝叶斯神经网络的分类任务以及标准电影数据集的在线贝叶斯矩阵分解。 我们的实验结果证明了该算法的有效性。
2. Hamiltonian Monte Carlo
2.哈密尔顿蒙特卡洛
假设我们想从θ的后验分布中给出一组独立的观察x∈D:
势能函数U由下式给出:
其中势能函数U由哈密顿(混合)蒙特卡罗(HMC)给出(Duane等,1987; Neal,2010)提供了一种在Metropolis-Hastings(MH)框架中提出θ样本的方法,该方法有效地探索了 状态空间与标准随机游走提案相比。 这些提议是基于引入一组辅助动量变量r的哈密顿系统生成的。 也就是说,从p(θ|D)进行采样,HMC考虑从由(θ,r)定义的联合分布生成样本。
如果我们简单地丢弃得到的r样本,则θ样本具有边际分布p(θjD)。 这里,M是质量矩阵,与r一起定义了动能项。 M通常设置为单位矩阵I,但是当我们有关于目标分布的更多信息时,可以用来预处理采样器。 哈密顿函数由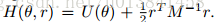
为了提出样本,HMC模拟哈密顿动力学
使Eq(4)具体,2D中常见的类比如下(Neal,2010)。 想象一下,冰球在不同高度的无摩擦冰面上滑动。 势能项基于当前圆盘位置的表面高度θ,而动能基于圆盘的动量r及其质量M.如果表面是平的(▽U( θ)= 0,∀θ),圆盘以恒定速度移动。 对于正斜率(▽U(θ)> 0),动能随着势能增加而减小,直到动能为0(r = 0)。 然后冰球向下滑回山坡,增加其动能并降低势能。 回想一下,在HMC中,位置变量是直接感兴趣的,而动量变量是人工构造(辅助变量)。
在任何时间间隔s,方程的哈密顿动力学。 (4)定义从时间t的状态到时间t + s的状态的映射。 重要的是,这种映射是可逆的,这对于表明动力学留下π不变性很重要。 同样,动态保留了总能量H,因此总是接受建议。 然而,在实践中,我们通常无法从方程的连续系统中精确地模拟。 (4)而是考虑一个离散化的系统。 一种常见的方法是“蛙跳”方法,该方法在Alg中概述。 1.由于通过离散化引入的不准确性,必须实施MH步骤(即,接受率不再是1)。 然而,即使对于距离上一个州很远的提案,接受率仍然很高。
HMC最近有许多发展,使算法更灵活,适用于各种环境。 “No U-Turn”采样器(Hoffman&Gelman,2011)和Wang等人提出的方法。 (2013)允许自动调整步长,和模拟步骤的数量,m。 黎曼流形HMC(Girolami&Calderhead,2011)利用黎曼几何来适应质量M,使算法能够利用曲率信息来执行更有效的采样。 我们尝试在重点关注计算复杂性的正交方向上改进HMC,但是这些自适应HMC技术可能与我们提出的方法相结合以获得进一步的益处。
3. Stochastic Gradient HMC
在本节中,我们研究了使用随机梯度实现HMC的含义,并提出了哈密顿动力学的变量,这些变量对随机梯度估计引入的噪声更具鲁棒性。 在所有场景中,不是使用Eq直接计算昂贵的梯度▽U(θ)。 (2),这需要检查整个数据集D,我们考虑基于从D随机均匀采样的小批量D的噪声估计:
我们假设我们的观察x是独立的,并且吸引中心极限定理,将这个噪声梯度近似为
这里,V是随机梯度噪声的协方差,其可以取决于当前模型参数和样本大小。 请注意,我们在方程式中滥用符号。 (6)其中N(μ;Σ)的加法表示引入根据该多元高斯分布的随机变量。 随着D~的大小增加,这种高斯近似变得更准确。 显然,我们希望小型小型机具有我们广受欢迎的计算收益。 根据经验,在广泛的设置中,简单地考虑数百个数据点的小批量大小就足以使中心极限定理近似准确(Ahn等,2012)。 在我们感兴趣的应用中,这种尺寸的小批量仍然代表了梯度计算成本的显着降低。
3.1. Na¨ıve Stochastic Gradient HMC
随机梯度HMC最直接的方法是简单地替换Alg中的▽U(θ)。 1 by▽U~(θ)。 参考Eq。 (6),这在动量更新中引入噪声,其变为Δr=-ε▽U~(θ)=-ε▽U(θ)+ 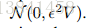
这里,B(θ)= 1 /2εV(θ)是由梯度噪声贡献的扩散矩阵。 与原始HMC配方一样,返回连续时间系统以获得方法的属性是有用的。 为了获得关于此设置的一些直觉,请考虑与Sec相同的曲棍球冰球类比。 在这里,我们可以想象冰球在同一个冰面上,但也有随风吹动。 这种风可能使冰球比预期的更远。 形式上,如定理3.1的推论3.1所给出的,当B非零时,等式3的π(θ,r)在等式7描述的动力学下不再是不变的。
定理3.1。 设pt(θ; r)为时间t处的(θ,r)分布,其动力学由等式1控制。(7)。 将pt的熵定义为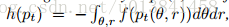
等式8表示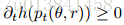
直觉上,定理3.1是正确的,因为无噪声哈密顿动力学保留熵,而附加噪声项严格增加熵如果我们假设(i)B(θ)是正定(由于Fisher的正常满秩性质的合理假设) 信息)和(ii)▽rpt(θ,r)6!= 0表示所有t。 然后,联合,熵随时间严格增加。 这暗示了分布pt倾向于均匀分布的事实,其可以非常远离目标分布π。
推论3.1。 在等式7的动力学下,分布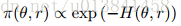
定理3.1和推论3.1的证明在补充材料中。
因为π在等式7的动力学下不再是不变的,所以我们必须在考虑动力系统离散化引入的误差之前引入校正步骤。为了MH步骤的正确性(基于整个数据集),我们呼吁为Neal(2010)的HMC数据分裂技术提出相同的论点。该方法同样考虑小批量数据并且顺序地模拟每个批次的(连续)哈密顿动力学。重要的是,Neal(2010)提到这样一个事实,即分裂数据场景中产生的H可能远远低于仿真后的全数据场景,这导致较低的接受率,从而降低了模拟中的表观计算收益。根据经验,正如我们在图2中所示,我们发现即使是来自噪声系统的有限长度模拟也可以与无噪声系统的模拟发生很大差异。虽然本文考虑的基于迷你型的HMC技术与Neal(2010)略有不同,但我们在定理3.1中开发的理论围绕等式7的最终不变分布的高熵特性,为观察到的偏差提供了一些直觉。在我们的实验和Neal(2010)的H中。
基于使用噪声梯度的模拟的H轨迹的表现不佳的特性导致复杂的计算与效率权衡。一方面,在大型数据集中,在短暂的模拟运行之后插入MH步骤是非常计算密集的(其中H的偏差不太明显,接受率应该合理)。这些MH步骤中的每一步都需要使用所有数据进行昂贵的计算,从而破坏了考虑噪声梯度的计算增益。另一方面,MH步骤之间的长时间模拟运行会导致非常低的接受率。每个拒绝对应于使用所提出的Alg变体的浪费(噪声)梯度计算和模拟。 1.未来研究的一个可能的方法是考虑使用Korattikara等人的最新结果。 (2014年)和Bardenet等人。 (2014)表明可以使用数据子集进行MH。但是,我们反而考虑在Sec。 3.2对哈密顿动力学的直接修改,减轻了随机梯度引入的噪声问题。特别是,我们的修改允许我们再次实现所需的π作为连续哈密顿动力系统的不变分布。
3.2. Stochastic Gradient HMC with Friction
3.2。 具有摩擦力的随机梯度HMC
在第二节 在图3.1中,我们表明具有随机梯度的HMC需要频繁昂贵的MH校正步骤,或者可选地,具有低接受概率的长模拟运行。 理想情况下,我们希望尽量减少注入噪声对动态本身的影响,以缓解这些问题。 为此,我们考虑对等式7进行修改,为动量更新添加“摩擦”术语:
在本文的其余部分,为了简化符号,我们省略了B对θ的依赖性。 让我们再做一个曲棍球比喻。 想象一下,我们现在正在玩街头曲棍球而不是冰球,这会引起沥青的摩擦。 仍然存在随机吹风,但是表面的摩擦阻止了冰球远离。 也就是说,摩擦项BM -1r有助于减小能量H(θ,r),从而减小噪声的影响。 这种类型的动力系统通常被称为物理学中的二阶Langevin动力学(Wang&Uhlenbeck,1945)。 重要的是,我们注意到SGLD中使用的Langevin动力学(Welling&Teh,2011)是一阶的,当摩擦项很大时,可以将其视为我们二阶动力学的极限情况。 有关此比较的更多详细信息,请参见本节末尾。
定理3.2。 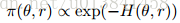
证明。 设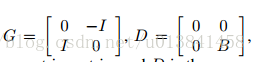
该动力系统下的分布演化由Fokker-Planck方程控制
有关详细信息,请参阅补充材料。 我们可以验证π(θ,r)在方程式下是不变的。 (10)通过计算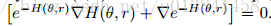
总之,我们已经证明等式(9)给出的动力学具有与等式(4)的原始哈密顿动力学相似的不变性,即使存在噪声也是如此。 关键是使用二阶Langevin动力学引入摩擦项。 我们修订的动量更新也可以被视为类似于部分动量更新(Horowitz,1991; Neal,1993),这也对应于二阶Langevin动力学。 在无噪声梯度的情况下,这种部分动量刷新被证明不会大大改善HMC(Neal,2010)。 然而,正如我们已经证明的那样,这个想法在我们的随机梯度情景中是至关重要的,以抵消噪声梯度的影响。 我们将得到的方法称为随机梯度HMC(SGHMC)。
与一阶LANGEVIN动力学的联系
正如我们之前所讨论的,等式(9)中引入的动力学与SGLD中使用的一阶Langevin动力学有关(Welling&Teh,2011)。 特别是,SGLD的动态可以被视为具有大摩擦项的二阶Langevin动力学。 为了直观地证明这种连接,让等式(9)中的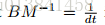
r的快速演化导致等式(11)的平稳分布的快速收敛,其由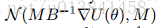
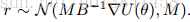
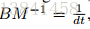
这与SGLD的动态完全一致,其中M -1作为预处理矩阵(Welling&Teh,2011)。 直觉上,这意味着当摩擦力很大时,动力学不依赖于dr所代表的过去梯度的衰减序列,而是降低到一阶Langevin动力学。
3.3. Stochastic Gradient HMC in Practice
在我们到目前为止所考虑的一切中,我们假设我们知道噪声模型B.显然,实际情况并非如此。 想象一下,我们只是简单地拥有一个B ^。 如将变得清楚的,替代地引入用户指定的摩擦项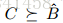
得到的SGHMC算法显示在Alg中。 2.请注意,该算法纯粹是根据用户指定或可计算的数量。 为了理解我们对动力学的选择,我们从完美估计B的不切实际的场景开始。
命题3.1。 如果B ^ = B,那么等式(13)的动力学产生静止分布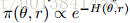
证明。 动量更新简化为r = 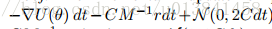
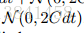
现在考虑在B的不准确估计的更现实的情况下引入C项和修正动力学的好处。例如,最简单的选择是B ^ = 0.尽管真正的随机梯度噪声B显然不为零,但是 步长ε - > 0,B = 1 /2εV变为0且C占优势。 也就是说,动力学再次受可控注入噪声N(0,2Cdt)和摩擦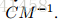
计算复杂性
Alg.2的复杂性取决于M,C和^ B的选择,估计者▽~U(θ)的复杂度 - 表示为g(| D |,d) - 其中d是参数空间的维数。 假设我们允许^ B是任意d * d正定矩阵。 使用^ B的经验Fisher信息估计,该估计步骤的每迭代复杂度为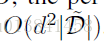
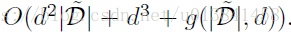
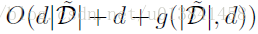
在实践中,我们必须假设B的估计不准确。对于衰减的一系列步长εt,不需要MH步骤(Welling&Teh,2011; Ahn等,2012)1。 然而,随着步长减小,采样器的效率同样降低,因为提议越来越接近其初始值。 在实践中,我们可能希望容忍采样精度中的一些误差以获得效率。 与SGLD中的(Welling&Teh,2011; Ahn等,2012)一样,我们考虑使用一个小的非零ε导致一些偏差。 我们探讨了对补充材料中这种有限ε近似引入的误差的分析。
与动力连接到SGD
为随机梯度下降(SGD)添加动量项是常见的做法。 从概念上讲,SGD与动力和SGHMC之间存在明确的关系,在这里我们将这种联系形式化。 让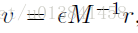
与具有动量法的SGD相比,从等式(15)可以清楚地看出,η对应于学习速率,而α对应于动量项。 当噪声被消除时(通过C = ^ B = 0),SGHMC自然地减少为具有动量的随机梯度方法。 我们可以使用等式(15)的等效更新规则来运行SGHMC,并借助SGD参数设置的经验来指导我们选择SGHMC设置。 例如,我们可以将α设置为固定的小数(例如,0.01或0.1),选择学习率η,然后确定^β=η^ V / 2。 更复杂的策略涉及使用动量调度(Sutskever等,2013)。 我们详细说明了如何在补充材料中选择这些参数。
图1.与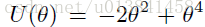
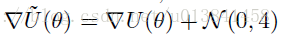
具有动量的梯度法。 我们可以使用Eq的等效更新规则。 (15)运行SGHMC,借鉴新元参数设置的经验,指导我们选择SGHMC设置。 例如,我们可以将α设置为固定的小数(例如,0.01或0.1),选择学习率η,然后确定^β=η^ V / 2。 更复杂的策略涉及使用动量调度(Sutskever等,2013)。 我们详细说明了如何在补充材料中选择这些参数。
4. Experiments
4.1. Simulated Scenarios4.1。 模拟场景
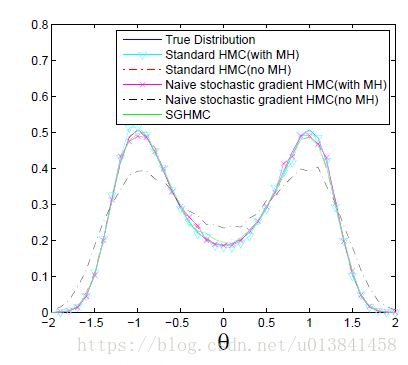
为了通过使用相对于随机梯度的精确梯度来实证地探索HMC的行为,我们在模拟设置上进行实验。作为基线,我们考虑Alg 1的标准HMC实现,有和没有MH校正。然后,我们将HMC与随机梯度进行比较,用▽~U代替Alg1中的▽U,并在有和没有MH校正的情况下考虑该提议。最后,我们将比较我们提出的SGHMC,它不使用MHM校正。图1显示了不同采样算法产生的经验分布。我们看到即使没有MH校正,HMC和SGHMC算法都提供接近真实分布的结果,这意味着考虑非零ε的任何误差都可以忽略不计。另一方面,除非增加MH校正,否则随机梯度HMC的结果与真实性显着不同。这些发现验证了我们的理论结果也就是说,标准HMC和SGHMC都将兀动作为不变分布保持为ε-> 0,而随机梯度HMC则没有,尽管这可以通过使用(昂贵的)MH步骤进行校正.
图2.使用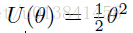
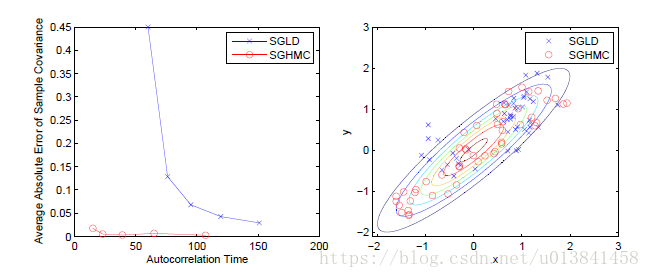
图3.使用SGHMC与SGLD的二元高斯的对比采样与相关性。 这里,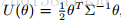
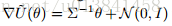
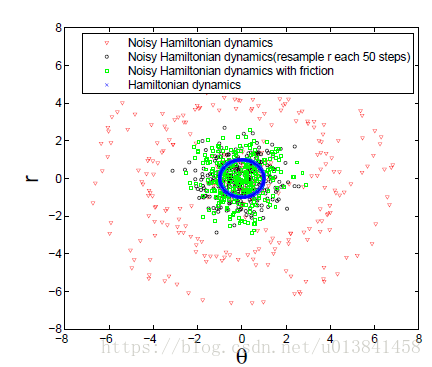
我们还考虑简单地模拟与各种采样器相关的离散化哈密顿动力系统。 在图2中,我们比较得到的轨迹,并看到来自没有摩擦的噪声系统的(θ,r)路径显着偏离。 通过添加摩擦(对应于SGHMC)来修改动力系统可以纠正这种行为。 我们也可以通过动量的周期性重新采样来校正这种偏差,尽管如图1所示,相应的MCMC算法(“朴素随机梯度HMC(无MH)”)不能产生正确的目标分布。 这些结果证实了摩擦项在维持良好的哈密顿量并导致正确的平稳分布方面的重要性。
众所周知,HMC相对于许多其他MCMC算法的好处是从相关分布中采样的效率(Neal,2010) - 这是动量变量引入的地方。 SGHMC继承了这个属性。图3比较了从具有正相关的双变量高斯采样时的SGHMC和SGLD(Welling&Teh,2011)。对于每种方法,我们以线性递减的比例检查初始步长的五种不同设置,并生成一千万个样本。对于这些样本集中的每一个(每步长设置一组),我们计算样本的自相关时间2和所得样本协方差的平均绝对误差。图3(a)显示了五种设置的自相关与估计误差。随着我们减小步长,SGLD具有相当低的估计误差,但是高自相关时间表明采样器效率低。相比之下,SGHMC在非常低的自相关时间内实现了更低的估计误差,从中我们得出结论,采样器确实有效地探索了分布。图3(b)显示了由两个采样器产生的前50个样本。我们看到SGLD的随机游走行为使探索分布的尾部具有挑战性。与SGHMC相关联的动量变量反而驱动采样器沿分布轮廓移动。
4.2. Bayesian Neural Networks for Classification
我们还使用MNIST数据集3在手写数字分类任务上测试我们的方法。该数据集由60,000个训练实例和10,000个测试实例组成。我们从训练数据中随机分割包含10,000个实例的验证集,以便选择训练参数,并使用剩余的50,000个实例进行训练。对于分类,我们考虑使用sigmoid单元和使用softmax的输出层的具有100个隐藏变量的两层贝叶斯神经网络。我们测试了四种方法:SGD,SGD with momentum,SGLD和SGHMC。对于基于优化的方法,我们使用验证集来选择网络权重的最优正则化因子4。对于基于采样的方法,我们采用完全贝叶斯方法,并在每个层的权重正则化器λ之前放置一个弱信息伽马。采样程序通过运行SGHMC和SGLD使用500个训练实例的小批量进行,然后在整个训练集通过后重新采样超参数。我们运行采样器800次迭代(每次都在整个训练数据集上)并丢弃最初的50个样本作为老化。
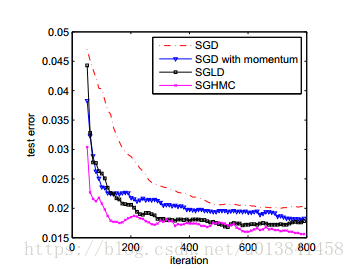
在图4中,针对这些方法中的每一种报告了作为MCMC的函数或优化迭代(在老化之后)的测试误差。从结果,我们看到具有动量的SGD收敛比SGD快。 SGHMC还具有优于SGLD的优势,可以更快地收敛到低测试误差。 就运行时而言,在这种情况下,反向传播中使用的梯度计算占主导地位,因此两者具有相同的计算成本。 基于采样的方法的最终结果优于基于优化的方法,在该设置中显示了贝叶斯推理的优势,从而验证了对可扩展且高效的贝叶斯推理算法(例如SGHMC)的需求。
图4.使用SGD,带动量的SGD,SGLD和SGHMC的MNIST数据集上的测试误差的收敛性,以推断贝叶斯神经网络的模型参数。
4.3. Online Bayesian Probabilistic Matrix Factorization for Movie Recommendations
4.3。 电影推荐的在线贝叶斯概率矩阵分解
协同过滤是Web应用程序中的一个重要问题。 任务是预测用户对一组项目(例如,电影,音乐)的偏好并产生推荐。 概率矩阵分解(PMF)(Salakhutdinov&Mnih,2008b)已证明对此任务有效。 由于推荐系统中评级矩阵(用户与项目)的稀疏性,过度拟合是贝叶斯方法提供自然解决方案的严重问题(Salakhutdinov&Mnih,2008a)。
我们在Movielens数据集ml-1M5上进行了在线贝叶斯PMF的实验。该数据集包含6,040个用户的3,952部电影的约100万个评级。潜在维度的数量设置为20.在比较基于随机梯度的方法时,我们使用4,000个评级的小批量来更新用户和项目潜在矩阵。由于与PMF模型相关的显着更大的参数空间,我们在此应用中选择比神经网络大得多的小批量大小。对于基于优化的方法,使用交叉验证来设置超参数(同样,我们没有看到与考虑MAP估计的性能差异)。对于基于采样的方法,超参数在每2个之后使用吉布斯步骤更新;采样模型参数的000步骤。我们运行采样器以生成2,000,000个样本,将前100,000个样本作为老化丢弃。我们使用五重交叉验证来评估不同方法的性能。
结果如表1所示.SGHMC和SGLD都比基于优化的方法提供更好的预测结果。 在本实验中,SGLD和SGHMC的结果非常相似。 我们还观察到两种方法的每次迭代运行时间是可比较的。 因此,该实验表明SGHMC是在线贝叶斯PMF的有效候选者。
5. Conclusion
在分布模式之间移动是基于MCMC的推理算法的关键挑战之一。为了在大规模或在线环境中解决这个问题,我们提出了SGHMC,这是一种在这种采样方法中产生高质量“远程”步骤的有效方法。我们的方法建立在HMC的基本框架之上,但使用梯度的随机估计来避免昂贵的全梯度计算。令人惊讶的是,我们发现将随机梯度估计结合到HMC中的自然方法可能导致理论上和实践中的差异和不良行为。为了应对这一挑战,我们引入了具有摩擦项的二阶Langevin动力学,该摩擦项抵消了噪声梯度的影响,将所需的目标分布保持为连续系统的不变分布。我们在模拟实验和实际数据中的实证结果验证了我们的理论,并证明了引入这种简单修改的实际价值。自然的下一步是探索将自适应HMC技术与SGHMC相结合。更广泛地说,我们认为有效优化和采样技术的统一,例如本文所述的那些技术,将能够实现贝叶斯方法的显着缩放。
Acknowledgements
这项工作部分得到了MARCO和DARPA赞助的TerraSwarm研究中心,ONR Grant N00014-10-1-0746,AFARR,NSF IIS-1258741和英特尔ISTC大数据协商的DARPA Grant FA9550-12-1-0406的支持。 我们也很欣赏与Mark Girolami,Nick Foti,Ping Ao和Hong Qian的讨论。