机器学习技法第四周学习笔记

1.Motivation and Primal Problem
之前我们学习的Hard-Margin SVM要求所有的数据都必须得正确分开，如下图所示，给定的数据并不能够被一条直线完全分开，所以SVM用线型核可能得不到解，从而得用高次核得到如右图所示的分类效果，但是右边的分类器及其可能过拟合。所以Hard-Margin SVM不适用于不能完全被分开的数据集。

而实践中碰到的数据集大部分都是不可完全分割的，所以为此人们提出了soft-Margin SVM.
如机器学习基石里面的pocket分类器，我们将条件要求降低，我们不再要求数据得全部分正确，而是转而要求分错的数据点要最低。于是得到下图下方所示的公式，对于分对的数据点，我们依据要求求得最大的margin，而对于分错的点，我们忽略然后对结果进行一定的惩罚，而用常数项c来调控惩罚的力度。比如我们对数据进行SVM分类，其中一个结果margin很大，但是里面有8个点被分错，而另一个结果margin相对小一点，但是其没有分错的点，这时就得靠C来决定选哪个结果，如果C很小那么选择前者，如果C很大那么选择后者。

但是以上式子有如下几个问题：
1.其优化式子和条件不再是二次式和一次式，所以该问题不再是二次规划问题，所以我们之前所推倒的东西都不在适用该问题。
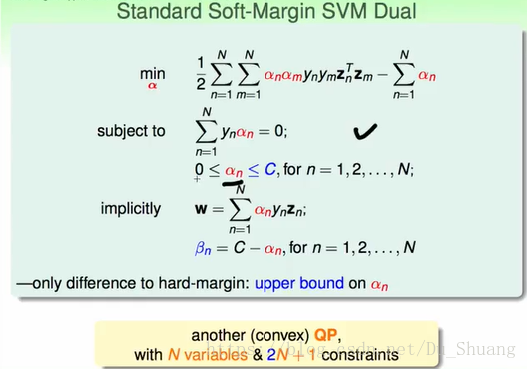
2.上述式子只能区分分错点的个数，而不能区分大错和小错，于是我们将上诉式子进行变形求出其对偶问题，如下图所示。
我们用ζ来表示点的错误程度即离最小边界的距离。用其和来决定惩罚项的大小，这时ζ和C共同决定惩罚项的大小其中C人为指定。

这时之前存在的两个问题就都不存在了。
这时新QP式子的变量增加了N个主要是用来确定错误大小的ζ，条件也增加了N个主要是保证ζ必须大于0。

2.Dual Problem
接下来我们来推导上式的对偶问题，首先写出拉格朗日式子，然后求其最大最小，然后交换最大最小的顺序变为最大最小的强对偶问题（这时求(w,b,ζ)将没有条件）。

同样对变量求导带入化简：

这时我们发现化简的式子与Hard-Margin SVM的式子一样只是条件$α_n$的范围变了。
于是我们可以将之前的推导直接照搬过来得到如下结果：

3.Messages behind Soft-Margin SVM
接下来我们将求解上面求得的二次规划式子，我们知道上面的二次规划式子和hard-margin-svm是一样的（除了条件有一点差别），所以我们求α的过程是能照搬的。

但是我们在利用kkt条件求解b的时候会产生区别因为我们的soft svm里面多了个ζ，而这个参数是和β（转换为与α）有关的，这样我们将α分为几种情况。
当α大于0我们称之为SV，当α小于C我们称之为free SV，而只有free SV才能求得(b).

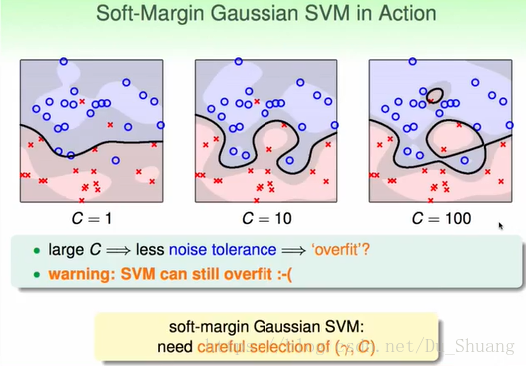
下面我们来分析C对结果的影响。
我们发现C越大，对错误越严格于是更容易过拟合。

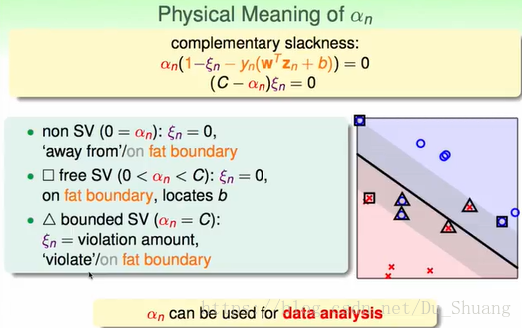
接下来我们来分析不同的α代表的物理意义：
对于free SV($0<α_n<C$):ζ=0,所以其代表的点刚好在边界上。
对于 non SV(0=$α_n$):ζ=0,所以其代表分类正确且远离于边界的点。
对于bounded SV($α_n$=C)：$ζ=1-y(w^Tz_n+b)$,所以其代表分类 错误的点离边界的距离。

4.Model Selection
下图为用Gaussian Kernel 做的SVM分类，其中横轴为C惩罚系数，纵轴为γ即Gaussian Kernel的系数。
那么我们该怎么选择C和γ呢?

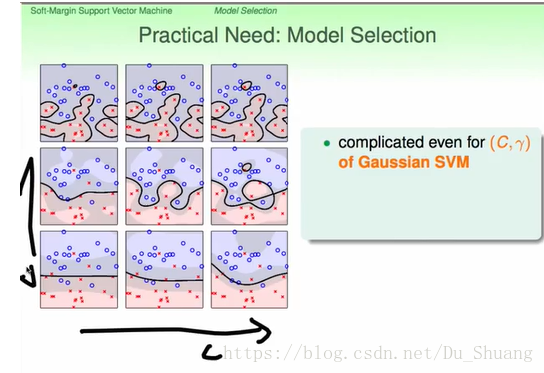
那么我们可以用我们之前的validation来进行选择判断，结果如下图所示。

我们发现当我们使用leave one out validation进行验证时，$E_loocv$的大小会小于SV的比例，证明如下：
因为对于looc非SV去掉后，其结果不会受到影响，所以验证的结果一定是对的。
只有当验证的结果为SV时，才有可能出错，所以其上限为sv在总点中的比例。

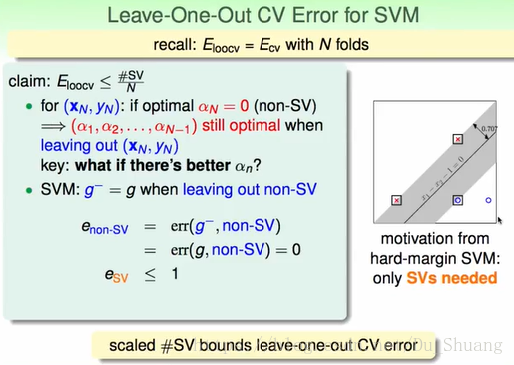
那么上面这个性质有什么用呢？
上面那个性质能够帮助我们对SVM的结果做初步的判断，当我么求得的SVM有较多的SV时，我们的分类结果较大可能是错的。