Learning Kalman filter

by luoshi006

参考：A practical approach to Kalman filter and how to implement it、 Kalman filter wikiPedia

参考 PX4 中 EKF 的matlab实现，并将代码注释于第6节。

1、 introduction

http://mathworld.wolfram.com/KalmanFilter.html

2、预备知识

3、定义

卡尔曼滤波器，是一种高效的递归滤波器，其输入是一组随时间变化观测到的数值序列（如：加速度计、陀螺仪），这些观测值包含噪声。卡尔曼滤波器基于当前和前一时刻的状态，估计出更为精确的系统状态。

这种滤波方法以它的发明者鲁道夫.E.卡尔曼（Rudolph E. Kalman）命名。

4、噪声来源

加速度计：
当机器人往复运动时，测量的重力加速度会有很多噪声。

陀螺仪：
它随着时间漂移。（就像旋转的陀螺失速时，转轴指向无法维持）【这个栗子(+﹏+)~】

简单说来，就是短时间内，陀螺仪的数据可信度高；长时间以后，加速度计的数据可信度高。

互补滤波
这种情况下，互补滤波器是种比较简单的处理方法。基本原理就是：对加速度计的数据低通滤波，对陀螺仪的数据高通滤波。它没有卡尔曼滤波器准确，但经过调节，也能够简单使用。

互补滤波器和卡尔曼滤波器的对比：

参考： blog

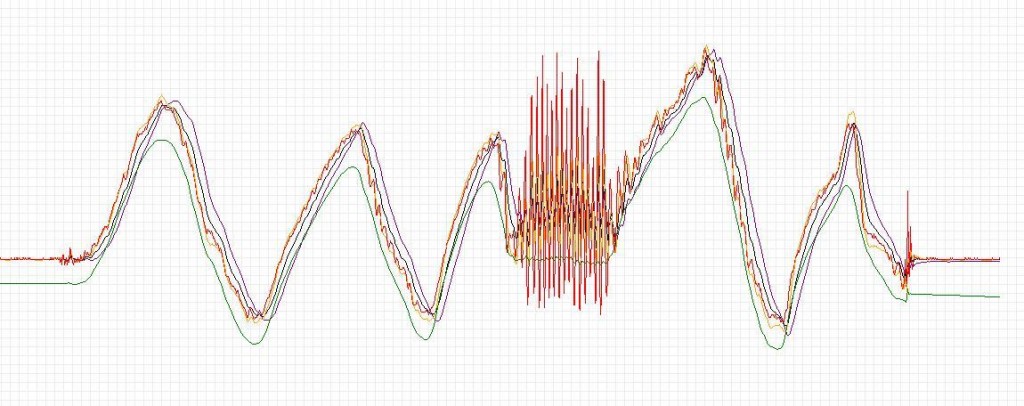
curve
图中：
红色：加速度计；绿色：陀螺仪；蓝色：卡尔曼滤波；黑色：互补滤波；黄色：二阶互补滤波；

可以看到，由于振动的影响，加速度计已被振傻，而陀螺仪的数据越来越飘~

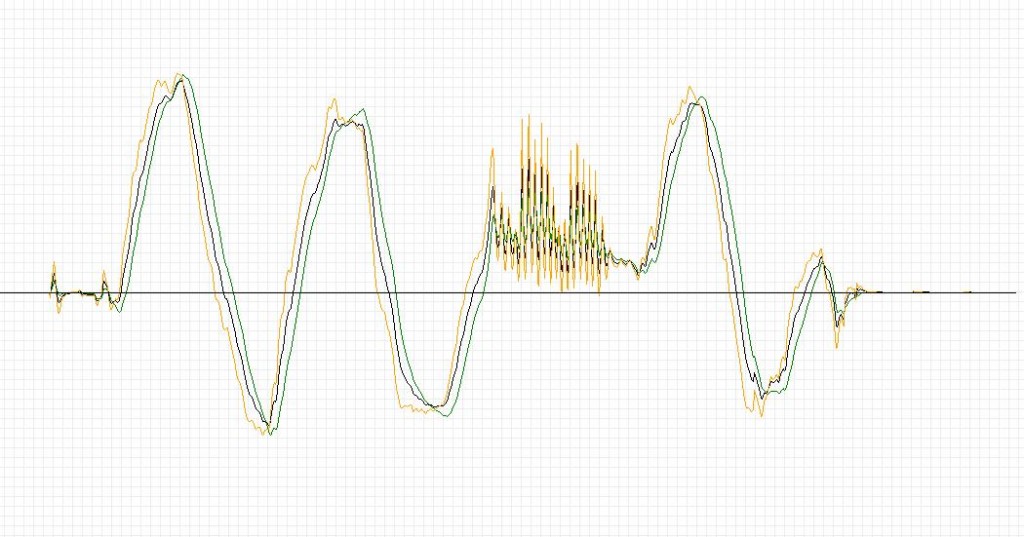
filter
图中：
绿色：卡尔曼；黑色：互补滤波；黄色：二阶互补滤波；

卡尔曼滤波比互补滤波多了延时，但更适应振动。二阶互补滤波曲线不理想，可能是参数的问题。

5、符号定义

卡尔曼滤波是对观测量的最优估计。首先，它需要知道观测器的测量噪声（measurement noise）和系统的过程噪声（process noise）。这些噪声必须是高斯分布，且均值为零。幸运的是，大部分随机噪声都有这些特性。

更多卡尔曼滤波信息：

wikiPedia Kalman filter

An Introduction to the Kalman Filter

Kalman Filtering Embedded Systems Programming

5.1 系统状态 $x_k$

文中使用的符号沿用wikiPedia Kalman filter。

其中，常数矩阵（与时间无关），不需要标下标 $k$ 。即， $F_k$ 表示为 $F$ 。
另外，还有一些记号表示的解释：

上一时刻状态（previous state）
${\hat{x}}_{k - 1 ∣ k - 1}$ $\hat{x}_{k-1\mid k-1}$

表示： $k-1$ 时刻，状态的最优估计

预测状态（先验状态）（priori state）
${\hat{x}}_{k ∣ k - 1}$ $\hat{x}_{k\mid k-1}$

表示： $k$ 时刻，状态的最优预测；由之前的状态和估计得到当前 $k$ 时刻的状态矩阵估计值。

校正状态（后验状态）（posteriori state）
${\hat{x}}_{k ∣ k}$ $\hat{x}_{k\mid k}$

表示： $k$ 时刻，状态的最优估计；由 $k$ 时刻的观测值校正后的最优估计。

提出问题：系统状态不能直接得到，只能通过观测值 $z_k$ 得到。称为：隐马儿可夫模型Hidden Markov model
这就意味着，系统状态只能由当前时刻观测值和之前所有的观测状态得到。同时，在卡尔曼滤波稳定之前，得到的状态估计是不可信的。

$\hat{x}$ 表示状态的估计值；
$x$ 表示状态的真实值（希望得到的值）；

故：

$k$ 时刻状态表示为：

$x_{k}$ $x_k$
$k$ 时刻的系统状态由该式给出：

$x_{k} = F x_{k - 1} + B u_{k} + w_{k}$ $x_k = F x_{k-1} + B u_k + w_k$
$x_k$ 是状态矩阵：

$x_{k} = {[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k}$ $x_k = \begin{bmatrix} \theta \\ \dot{\theta}_b\\ \end{bmatrix}_k$

所以，滤波器的输出是角度 $\theta$ 和偏差 $\dot{\theta}_b$ 。偏差为陀螺仪的偏移量。所以，有陀螺仪的测量值减去该偏差，就得到真是的速度值。

$F$ 矩阵，状态转换模型，用于上一时刻状态：

$F = [\begin{matrix} 1 & - Δ t \\ 0 & 1 \end{matrix}]$ $F= \begin{bmatrix}1 & -\Delta t \\ 0 & 1 \\ \end{bmatrix}$
$u_k$ 是系统输入。本文中，它表示陀螺仪在 $k$ 时刻的读数（单位：°/s），也被称为角速度 $\dot{\theta}$ 。
系统状态可重写为：

x_{k} = F x_{k - 1} + B {\dot{θ}}_{k} + w_{k}

$x_k=Fx_{k-1}+B\dot{\theta}_k+w_k$

其中，矩阵 $B$ 为控制/输入矩阵，定义为：

B = [\begin{matrix} Δ t \\ 0 \end{matrix}]

$B=\begin{bmatrix}\Delta t\\ 0 \\ \end{bmatrix}$

矩阵 $B$ 中的 $\Delta t$ 乘以角速度 $\dot{\theta}$ 可以得到角度 $\theta$ 。但是，偏差（bias）无法直接由角速度计算得到，所以矩阵 $B$ 底部元素设为0.

$w_k$ 是过程噪声，均值为0的高斯分布，协方差 $Q$ 与时间 $k$ 相关：

w_{k} \sim N (0, Q_{k})

$w_k \sim N(0,Q_k)$

其中， $Q_k$ 是过程噪声的协方差矩阵。在本文中，表示为加速度计和偏差的状态估计的协方差矩阵。本文认为偏差和加速度计的估计是独立的，所以，协方差等于加速度计和偏差的方差的乘积。
最终得到：

Q_{k} = [\begin{matrix} Q_{θ} & 0 \\ 0 & Q_{\dot{θ}} \end{matrix}] Δ t

$Q_k=\begin{bmatrix}Q_{\theta} & 0 \\ 0 & Q_{\dot{\theta}} \end{bmatrix} \Delta t$

可以看出， $Q_k$ 协方差矩阵随时间变化，所以，加速度计方差 $Q_\theta$ 和偏差的方差 $Q_{\dot{\theta}_b}$ 需要乘以时间变化量 $\Delta t$ 。
所以，距离上一次状态更新的时间越长，过程噪声会越大。例如：陀螺仪的漂移。【??? 存疑，待修正】。

必须知道卡尔曼滤波运行所需要的常数（值越大，状态估计的噪声越大）：
例如，如果估计的角度开始漂移，就必须增大 $Q_{\dot{\theta}_b}$ 的值。如果状态变化较慢，角度的估计更加可信，应该减小 $Q_\theta$ ，增大加速度计可信度。

5.2 观测值 $z_k$

现在开始考虑真实状态 $x_k$ 的观测值 $z_k$ 。
观测方程由下式给出：

z_{k} = H x_{k} + v_{k}

$z_k=Hx_k+v_k$

式中，观测值 $z_k$ 由当前状态 $x_k$ 乘以矩阵 $H$ ，再加上测量噪声 $v_k$ 。
矩阵 $H$ 是观测模型，用于将真实的状态映射到观测空间。因为，真实状态是不可直接获取的，测量值是加速度计的读数（加速度角度），

H = [\begin{matrix} 1 & 0 \end{matrix}]

$H=\begin{bmatrix}1&0 \end{bmatrix}$

测量噪声 $v_k$ 认为是高斯分布（正态分布），期望为0，协方差为 $R$ ：

v_{k} \sim N (0, R)

$v_k \sim N(0,R)$

以下部分待验证

相同变量的协方差等于其方差，当 $R$ 不是矩阵时，就等于测量值的方差。详情参见协方差矩阵的符号分歧。定义 $R$ ：

R = E [\begin{matrix} v_{k} & v_{k}^{T} \end{matrix}] = v a r (v_{k})

$R=E \begin{bmatrix} v_k&v_k^T\end{bmatrix}=var(v_k)$

假设测量噪声不随时间变化：

v a r (v_{k}) = v a r (v)

$var(v_k)=var(v)$

需要注意的是，如果将测量噪声值 $var(v)$ 设的太高，滤波器响应时间会变慢，因为新的测量值可信度较低；如果设的太低，可能会造成超调，引入大量噪声，因为此时加速度计可信度较高。

所以，找到过程噪声方差 $Q_\theta$ 、 $Q_{\dot{\theta}_b}$ 和测量噪声 $var(v)$ 十分重要。方法较多，另行开盘。。。

5.3 `AttitudeEKF.m`

以 px4 中的 EKF 代码为例。（该部分代码有matlab生成，在新版中已删除）

function [xa_apo,Pa_apo,Rot_matrix,eulerAngles,debugOutput]...
    = AttitudeEKF(approx_prediction,use_inertia_matrix,zFlag,dt,z,q_rotSpeed,q_rotAcc,q_acc,q_mag,r_gyro,r_accel,r_mag,J)

%LQG Position Estimator and Controller
% Observer:
%        x[n|n]   = x[n|n-1] + M(y[n] - Cx[n|n-1] - Du[n])
%        x[n+1|n] = Ax[n|n] + Bu[n]
%
% $Author: Tobias Naegeli $    $Date: 2014 $    $Revision: 3 $
%
%
% Arguments:
% approx_prediction: if 1 then the exponential map is approximated with a
% first order taylor approximation. has at the moment not a big influence
% (just 1st or 2nd order approximation) we should change it to rodriquez
% approximation.
% 预测近似方式，1 -- 一阶泰勒展开，
% use_inertia_matrix: set to true if you have the inertia matrix J for your
% quadrotor
% 是否使用转动惯量矩阵；
% xa_apo_k: old state vectotr
% 之前状态向量
% zFlag: if sensor measurement is available [gyro, acc, mag]
% 传感器信号可用（测量值）
% dt: dt in s 秒
% z: measurements [gyro, acc, mag]
% 测量值
% q_rotSpeed: process noise gyro
% 陀螺仪角速度 过程噪声 Q
% q_rotAcc: process noise gyro acceleration
% 陀螺仪角加速度 过程噪声 Q
% q_acc: process noise acceleration
% 加速度 过程噪声 Q
% q_mag: process noise magnetometer
% 磁力计 过程噪声 Q
% r_gyro: measurement noise gyro
% 陀螺仪 测量噪声 R
% r_accel: measurement noise accel
% 加速度计 测量噪声 R
% r_mag: measurement noise mag
% 磁力计 测量噪声 R
% J: moment of inertia matrix
% 惯性矩，惯性积？


% Output:

% xa_apo: updated state vectotr
% 状态向量
% Pa_apo: updated state covariance matrix
% 状态协方差
% Rot_matrix: rotation matrix
% 旋转矩阵
% eulerAngles: euler angles
% 欧拉角
% debugOutput: not used 调试用；


%% model specific parameters

初始化变量：

% compute once the inverse of the Inertia
% persistent 申明静态变量；
persistent Ji;
if isempty(Ji)
    Ji=single(inv(J));
end

%% init
%  起飞时的初始值；
persistent x_apo
if(isempty(x_apo))
    gyro_init=single([0;0;0]);
    gyro_acc_init=single([0;0;0]);
    acc_init=single([0;0;-9.81]);
    mag_init=single([1;0;0]);
    % NED 中指北；
    x_apo=single([gyro_init;gyro_acc_init;acc_init;mag_init]);
    % single 转换为单精度；

end

persistent P_apo
if(isempty(P_apo))
    %     P_apo = single(eye(NSTATES) * 1000);
    P_apo = single(200*ones(12));
    % 200 表示 P 协方差很大，数据可信度低；
end

debugOutput = single(zeros(4,1));

%% copy the states
wx=  x_apo(1);   % x  body angular rate
wy=  x_apo(2);   % y  body angular rate
wz=  x_apo(3);   % z  body angular rate

wax=  x_apo(4);  % x  body angular acceleration
way=  x_apo(5);  % y  body angular acceleration
waz=  x_apo(6);  % z  body angular acceleration

zex=  x_apo(7);  % x  component gravity vector
zey=  x_apo(8);  % y  component gravity vector
zez=  x_apo(9);  % z  component gravity vector

mux=  x_apo(10); % x  component magnetic field vector
muy=  x_apo(11); % y  component magnetic field vector
muz=  x_apo(12); % z  component magnetic field vector

6、卡尔曼滤波器

卡尔曼滤波器，主要用于估计当前时刻 $k$ 的系统状态。主要分为预测、校正两步。

6.1 预测

状态预测

滤波器通过先前状态和陀螺仪的测量值，预测当前的状态。得到预测状态（先验状态priori state） $\hat{x}_{k \mid k-1}$

{\hat{x}}_{k ∣ k - 1} = F {\hat{x}}_{k - 1 ∣ k - 1} + B {\dot{θ}}_{k}

$\hat{x}_{k \mid k-1}=F \hat{x}_{k-1 \mid k-1}+B\dot{\theta}_k$

%% prediction section
% compute the apriori state estimate from the previous aposteriori estimate
%body angular accelerations
if (use_inertia_matrix==1)
    wak =[wax;way;waz]+Ji*(-cross([wax;way;waz],J*[wax;way;waz]))*dt;
else
    wak =[wax;way;waz];
end

%body angular rates
% 更新 角速度；
wk =[wx;  wy; wz] + dt*wak;

%derivative of the prediction rotation matrix
% 更新后的旋转矩阵 求导；
O=[0,-wz,wy;wz,0,-wx;-wy,wx,0]';

%prediction of the earth z vector
% 更新 加速度计 向量
% 任何旋转向量都可以表示为斜对称矩阵 O 的指数
% 这里的指数是以泰勒级数定义的矩阵乘法。O 矩阵叫做旋转的“生成元”
% 此部分概念请参考 【李代数】。

if (approx_prediction==1)
    %e^(Odt)=I+dt*O+dt^2/2!O^2
    % so we do a first order approximation of the exponential map
    zek =(O*dt+single(eye(3)))*[zex;zey;zez];

else
    zek =(single(eye(3))+O*dt+dt^2/2*O^2)*[zex;zey;zez];
    %zek =expm2(O*dt)*[zex;zey;zez]; not working because use double
    %precision
end



%prediction of the magnetic vector
if (approx_prediction==1)
    %e^(Odt)=I+dt*O+dt^2/2!O^2
    % so we do a first order approximation of the exponential map
    muk =(O*dt+single(eye(3)))*[mux;muy;muz];
else
     muk =(single(eye(3))+O*dt+dt^2/2*O^2)*[mux;muy;muz];
    %muk =expm2(O*dt)*[mux;muy;muz]; not working because use double
    %precision
end

% 预测状态：
x_apr=[wk;wak;zek;muk];

误差协方差预测

根据先前的误差协方差矩阵 $P_{k-1 \mid k-1}$ ，预测当前的先验误差协方差矩阵 $P_{k \mid k-1}$ ：

P_{k ∣ k - 1} = F P_{k - 1 ∣ k - 1} F^{T} + Q_{k}

$P_{k \mid k-1}=FP_{k-1 \mid k-1}F^T+Q_k$

该矩阵用于估计当前状态估计的可信度。值越小，当前状态估计的可信度越高。
由上式可知，如果不进行校正（更新），误差协方差会一直累积。

% compute the apriori error covariance estimate from the previous
%aposteriori estimate

EZ=[0,zez,-zey;
    -zez,0,zex;
    zey,-zex,0]';
MA=[0,muz,-muy;
    -muz,0,mux;
    muy,-mux,0]';

E=single(eye(3));
Z=single(zeros(3));

% 根据 状态向量 求出；
A_lin=[ Z,  E,  Z,  Z
    Z,  Z,  Z,  Z
    EZ, Z,  O,  Z
    MA, Z,  Z,  O];

A_lin=eye(12)+A_lin*dt;

%process covariance matrix

persistent Q
if (isempty(Q))
    Q=diag([ q_rotSpeed,q_rotSpeed,q_rotSpeed,...
        q_rotAcc,q_rotAcc,q_rotAcc,...
        q_acc,q_acc,q_acc,...
        q_mag,q_mag,q_mag]);
end

P_apr=A_lin*P_apo*A_lin'+Q;

6.2 校正

新息
首先，由当前的观测值 $z_k$ 和预测状态 $x_{k \mid k-1}$ 计算出新息：

{\tilde{y}}_{k} = z_{k} - H {\hat{x}}_{k ∣ k - 1}

$\widetilde y_k =z_k-H \hat{x}_{k \mid k-1}$

观测阵 $H$ 用于将预测状态 $x_{k \mid k-1}$ 映射到观测空间（加速度计观测）;

新息是向量形式【？】：

${\hat{y}}_{k} = {[\begin{matrix} \hat{y} \end{matrix}]}_{k}$ $\hat{y}_k=\begin{bmatrix}\hat{y}\end{bmatrix}_k$

%% update
if zFlag(1)==1&&zFlag(2)==1&&zFlag(3)==1

%     R=[r_gyro,0,0,0,0,0,0,0,0;
%         0,r_gyro,0,0,0,0,0,0,0;
%         0,0,r_gyro,0,0,0,0,0,0;
%         0,0,0,r_accel,0,0,0,0,0;
%         0,0,0,0,r_accel,0,0,0,0;
%         0,0,0,0,0,r_accel,0,0,0;
%         0,0,0,0,0,0,r_mag,0,0;
%         0,0,0,0,0,0,0,r_mag,0;
%         0,0,0,0,0,0,0,0,r_mag];
     R_v=[r_gyro,r_gyro,r_gyro,r_accel,r_accel,r_accel,r_mag,r_mag,r_mag];
    %observation matrix
    %[zw;ze;zmk];
    H_k=[  E,     Z,      Z,    Z;
        Z,     Z,      E,    Z;
        Z,     Z,      Z,    E];

    y_k=z(1:9)-H_k*x_apr;

新息协方差：

S_{k} = H P_{k ∣ k - 1} H^{T} + R

$S_k=HP_{k \mid k-1}H^T+R$

式中：观测阵 $H$ 用于将误差协方差预测矩阵 $P_{k \mid k-1}$ 映射到观测空间；
该式根据误差协方差预测矩阵 $P_{k \mid k-1}$ 和测量协方差矩阵 $R$ 估计出观测值的可信度。测量噪声越大， $S$ 的值越大。即，当前测量值可信度较低。

本文中， $S$ 是向量：

$S_{k} = {[\begin{matrix} S \end{matrix}]}_{k}$ $S_k=\begin{bmatrix}S\end{bmatrix}_k$

卡尔曼增益
卡尔曼增益用于表征新息的可信度。

K_{k} = P_{k ∣ k - a} H^{T} S_{k}^{- 1}

$K_k=P_{k \mid k-a}H^TS_k^{-1}$

可以得出，若新息可信度低，新息协方差 $S$ 较大；状态估计可信度高，误差协方差矩阵 $P$ 较小，此时，卡尔曼增益 $K_k$ 较小。反之，同理。
式中，观测阵 $H$ 的转置用于将误差协方差矩阵 $P$ 映射到观测空间。
启动时不知道状态，可以将误差协方差矩阵设为：

P = [\begin{matrix} L & 0 \\ 0 & L \end{matrix}] ， （ L ： l a r g e n u m b e r ）

$P=\begin{bmatrix} L & 0 \\ 0 & L\end{bmatrix}，（L：large number）$

若启动状态完全已知，且陀螺仪已校准，可将误差协方差矩阵初始化为零阵。

本文中，卡尔曼增益为2*1的矩阵：

$K = [\begin{matrix} K_{0} \\ K_{1} \end{matrix}]$ $K=\begin{bmatrix}K_0 \\ K_1 \end{bmatrix}$

    %S_k=H_k*P_apr*H_k'+R;
     S_k=H_k*P_apr*H_k';
     S_k(1:9+1:end) = S_k(1:9+1:end) + R_v;
    K_k=(P_apr*H_k'/(S_k));

校正

{\hat{x}}_{k ∣ k} = {\hat{x}}_{k ∣ k - 1} + K_{k} {\tilde{y}}_{k}

$\hat{x}_{k \mid k}=\hat{x}_{k \mid k-1}+K_k \widetilde y_k$

式中，新息 $\widetilde y_k$ 为观测值 $z_k$ 和预测状态 $\hat{x}_{k \mid k-1}$ 的差，所以，正负均有可能。

P_{k | k} = (I - K_{k} H) P_{k | k - 1}

$\boldsymbol{P}_{k | k} = (\boldsymbol{I} - \boldsymbol{K}_k \boldsymbol{H}) \boldsymbol{P}_{k | k-1}$

式中： $\boldsymbol{I}$ 为单位矩阵。

滤波器根据当前状态估计的可信度，修正误差协方差矩阵。使得可以由误差协方差预测矩阵 $P_{k | k-1}$ 和新息协方差 $S_k$ 得到系统状态。

    x_apo=x_apr+K_k*y_k;
    P_apo=(eye(12)-K_k*H_k)*P_apr;

7、参考文献中 Implement

A practical approach to Kalman filter and how to implement it

该部分的 C 代码，需根据实际系统修改。

step 1:

{\hat{x}}_{k | k - 1} = F {\hat{x}}_{k - 1 | k - 1} + B {\dot{θ}}_{k}

$\boldsymbol{\hat{x}}_{k | k-1} = \boldsymbol{F}\hat{x}_{k-1 | k-1} + \boldsymbol{B}{\dot{\theta}_k}$

{[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k | k - 1} = [\begin{matrix} 1 & - Δ t \\ 0 & 1 \end{matrix}] {[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k - 1 | k - 1} + [\begin{matrix} Δ t \\ 0 \end{matrix}] {\dot{θ}}_{k}

$\begin{bmatrix} \theta \\ \dot{\theta}_b \end{bmatrix}_{k | k-1} = \begin{bmatrix} 1 & -\Delta t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \theta \\ \dot{\theta}_b \end{bmatrix}_{k-1 | k-1} + \begin{bmatrix} \Delta t \\ 0 \end{bmatrix} \dot{\theta}_k$

= {[\begin{matrix} θ - {\dot{θ}}_{b} Δ t \\ {\dot{θ}}_{b} \end{matrix}]}_{k - 1 | k - 1} + [\begin{matrix} Δ t \\ 0 \end{matrix}] {\dot{θ}}_{k}

$= \begin{bmatrix} \theta - \dot{\theta}_b \Delta t \\ \dot{\theta}_b \end{bmatrix}_{k-1 | k-1} + \begin{bmatrix} \Delta t \\ 0 \end{bmatrix} \dot{\theta}_k$

= [\begin{matrix} θ - {\dot{θ}}_{b} Δ t + \dot{θ} Δ t \\ {\dot{θ}}_{b} \end{matrix}]

$= \begin{bmatrix} \theta - \dot{\theta}_b \Delta t + \dot{\theta} \Delta t \\ \dot{\theta}_b \end{bmatrix}$

= [\begin{matrix} θ + Δ t (\dot{θ} - {\dot{θ}}_{b}) \\ {\dot{θ}}_{b} \end{matrix}]

$= \begin{bmatrix} \theta + \Delta t (\dot{\theta} - \dot{\theta}_b) \\ \dot{\theta}_b \end{bmatrix}$

rate = newRate - bias;
angle += dt * rate;

step 2:

P_{k | k - 1} = F P_{k - 1 | k - 1} F^{T} + Q_{k}

$\boldsymbol{P}_{k | k-1} = \boldsymbol{F}\boldsymbol{P}_{k-1 | k-1}\boldsymbol{F}^T + \boldsymbol{Q}_k$

{[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k - 1} = [\begin{matrix} 1 & - Δ t \\ 0 & 1 \end{matrix}] {[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k - 1 | k - 1} [\begin{matrix} 1 & 0 \\ - Δ t & 1 \end{matrix}] + [\begin{matrix} Q_{θ} & 0 \\ 0 & Q_{{\dot{θ}}_{b}} \end{matrix}] Δ t

$\begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k-1} = \begin{bmatrix} 1 & -\Delta t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k-1 | k-1} \begin{bmatrix} 1 & 0 \\ -\Delta t & 1 \end{bmatrix} + \begin{bmatrix} Q_\theta & 0 \\ 0 & Q_{\dot{\theta}_b} \end{bmatrix}\Delta t$

= {[\begin{matrix} P_{00} - Δ t P_{10} & P_{01} - Δ t P_{11} \\ P_{10} & P_{11} \end{matrix}]}_{k - 1 | k - 1} [\begin{matrix} 1 & 0 \\ - Δ t & 1 \end{matrix}] + [\begin{matrix} Q_{θ} & 0 \\ 0 & Q_{{\dot{θ}}_{b}} \end{matrix}] Δ t

$= \begin{bmatrix} P_{00} - \Delta t P_{10} & P_{01} - \Delta t P_{11} \\ P_{10} & P_{11} \end{bmatrix}_{k-1 | k-1} \begin{bmatrix} 1 & 0 \\ -\Delta t & 1 \end{bmatrix} + \begin{bmatrix} Q_\theta & 0 \\ 0 & Q_{\dot{\theta}_b} \end{bmatrix}\Delta t$

= {[\begin{matrix} P_{00} - Δ t P_{10} - Δ t (P_{01} - Δ t P_{11}) & P_{01} - Δ t P_{11} \\ P_{10} - Δ t P_{11} & P_{11} \end{matrix}]}_{k - 1 | k - 1} + [\begin{matrix} Q_{θ} & 0 \\ 0 & Q_{{\dot{θ}}_{b}} \end{matrix}] Δ t

$= \begin{bmatrix} P_{00} -\Delta t P_{10} -\Delta t (P_{01} - \Delta t P_{11}) & P_{01} -\Delta t P_{11} \\ P_{10} -\Delta t P_{11} & P_{11} \end{bmatrix}_{k-1 | k-1} + \begin{bmatrix} Q_\theta & 0 \\ 0 & Q_{\dot{\theta}_b} \end{bmatrix}\Delta t$

= [\begin{matrix} P_{00} - Δ t P_{10} - Δ t (P_{01} - Δ t P_{11}) + Q_{θ} Δ t & P_{01} - Δ t P_{11} \\ P_{10} - Δ t P_{11} & P_{11} + Q_{{\dot{θ}}_{b}} Δ t \end{matrix}]

$= \begin{bmatrix} P_{00} -\Delta t P_{10} -\Delta t (P_{01} - \Delta t P_{11}) + Q_\theta \Delta t & P_{01} -\Delta t P_{11} \\ P_{10} -\Delta t P_{11} & P_{11} + Q_{\dot{\theta}_b} \Delta t \end{bmatrix}$

= [\begin{matrix} P_{00} + Δ t (Δ t P_{11} - P_{01} - P_{10} + Q_{θ}) & P_{01} - Δ t P_{11} \\ P_{10} - Δ t P_{11} & P_{11} + Q_{{\dot{θ}}_{b}} Δ t \end{matrix}]

$= \begin{bmatrix} P_{00} + \Delta t (\Delta t P_{11} - P_{01} - P_{10} + Q_\theta) & P_{01} -\Delta t P_{11} \\ P_{10} -\Delta t P_{11} & P_{11} + Q_{\dot{\theta}_b} \Delta t \end{bmatrix}$

P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle);
P[0][1] -= dt * P[1][1];
P[1][0] -= dt * P[1][1];
P[1][1] += Q_gyroBias * dt;

step 3:

{\tilde{y}}_{k} = z_{k} - H {\hat{x}}_{k | k - 1}

$\boldsymbol{\tilde{y}}_k = \boldsymbol{z}_k - \boldsymbol{H}\hat{x}_{k | k-1}$

= z_{k} - [\begin{matrix} 1 & 0 \end{matrix}] {[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k | k - 1}

$= \boldsymbol{z}_k - \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} \theta \\ \dot{\theta}_b \end{bmatrix}_{k | k-1}$

= z_{k} - θ_{k | k - 1}

$= \boldsymbol{z}_k - \theta_{k | k-1}$

y = newAngle - angle;

step 4:

S_{k} = H P_{k | k - 1} H^{T} + R

$\boldsymbol{S}_k = \boldsymbol{H} \boldsymbol{P}_{k | k-1} \boldsymbol{H}^T + \boldsymbol{R}$

= [\begin{matrix} 1 & 0 \end{matrix}] {[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k - 1} [\begin{matrix} 1 \\ 0 \end{matrix}] + R

$= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k-1} \begin{bmatrix} 1 \\ 0 \end{bmatrix} + \boldsymbol{R}$

= {P_{00}}_{k | k - 1} + R

$= {P_{00}}_{k | k-1} + \boldsymbol{R}$

= {P_{00}}_{k | k - 1} + v a r (v)

$= {P_{00}}_{k | k-1} + var(v)$

S = P[0][0] + R_measure;

step 5:

K_{k} = P_{k | k - 1} H^{T} S_{k}^{- 1}

$\boldsymbol{K}_k = \boldsymbol{P}_{k | k-1} \boldsymbol{H}^T \boldsymbol{S}_k^{-1}$

{[\begin{matrix} K_{0} \\ K_{1} \end{matrix}]}_{k} = {[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k - 1} [\begin{matrix} 1 \\ 0 \end{matrix}] S_{k}^{- 1}

$\begin{bmatrix} K_0 \\ K_1 \end{bmatrix}_k = \begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k-1} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \boldsymbol{S}_k^{-1}$

= {[\begin{matrix} P_{00} \\ P_{10} \end{matrix}]}_{k | k - 1} S_{k}^{- 1}

$= \begin{bmatrix} P_{00} \\ P_{10} \end{bmatrix}_{k | k-1} \boldsymbol{S}_k^{-1}$

= \frac{{[\begin{matrix} P_{00} \\ P_{10} \end{matrix}]}_{k | k - 1}}{S_{k}}

$= \dfrac{\begin{bmatrix} P_{00} \\ P_{10}\end{bmatrix}_{k | k-1}}{\boldsymbol{S}_k}$

注意：此处 $S$ 是标量，但 $S$ 可以是矩阵，此时，需要计算矩阵的逆。

K[0] = P[0][0] / S;
K[1] = P[1][0] / S;

step 6:

{\hat{x}}_{k | k} = {\hat{x}}_{k | k - 1} + K_{k} {\tilde{y}}_{k}

$\boldsymbol{\hat{x}}_{k | k} = \boldsymbol{\hat{x}}_{k | k-1} + \boldsymbol{K}_k \; \boldsymbol{\tilde{y}}_k$

{[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k | k} = {[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k | k - 1} + {[\begin{matrix} K_{0} \\ K_{1} \end{matrix}]}_{k} {\tilde{y}}_{k}

$\begin{bmatrix} \theta \\ \dot{\theta}_b \end{bmatrix}_{k | k} = \begin{bmatrix} \theta \\ \dot{\theta}_b \end{bmatrix}_{k | k-1} + \begin{bmatrix} K_0 \\ K_1 \end{bmatrix}_k \boldsymbol{\tilde{y}}_k$

= {[\begin{matrix} θ \\ {\dot{θ}}_{b} \end{matrix}]}_{k | k - 1} + {[\begin{matrix} K_{0} \tilde{y} \\ K_{1} \tilde{y} \end{matrix}]}_{k}

$= \begin{bmatrix} \theta \\ \dot{\theta}_b \end{bmatrix}_{k | k-1} + \begin{bmatrix} K_0 \; \boldsymbol{\tilde{y}} \\ K_1 \; \boldsymbol{\tilde{y}} \end{bmatrix}_k$

angle += K[0] * y;
bias += K[1] * y;

step 7:

P_{k | k} = (I - K_{k} H) P_{k | k - 1}

$\boldsymbol{P}_{k | k} = (\boldsymbol{I} - \boldsymbol{K}_k \boldsymbol{H}) \boldsymbol{P}_{k | k-1}$

{[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k} = ([\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] - {[\begin{matrix} K_{0} \\ K_{1} \end{matrix}]}_{k} [\begin{matrix} 1 & 0 \end{matrix}]) {[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k - 1}

$\begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k} = \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} K_0 \\ K_1 \end{bmatrix}_k \begin{bmatrix} 1 & 0 \end{bmatrix}\right) \begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k-1}$

= ([\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] - {[\begin{matrix} K_{0} & 0 \\ K_{1} & 0 \end{matrix}]}_{k}) {[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k - 1}

$= \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} K_0 & 0 \\ K_1 & 0 \end{bmatrix}_k \right) \begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k-1}$

= {[\begin{matrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{matrix}]}_{k | k - 1} - [\begin{matrix} K_{0} P_{00} & K_{0} P_{01} \\ K_{1} P_{00} & K_{1} P_{01} \end{matrix}]

$= \begin{bmatrix} P_{00} & P_{01} \\ P_{10} & P_{11} \end{bmatrix}_{k | k-1} - \begin{bmatrix} K_0 \; P_{00} & K_0 \; P_{01} \\ K_1 \; P_{00} & K_1 \; P_{01} \end{bmatrix}$

float P00_temp = P[0][0];
float P01_temp = P[0][1];

P[0][0] -= K[0] * P00_temp;
P[0][1] -= K[0] * P01_temp;
P[1][0] -= K[1] * P00_temp;
P[1][1] -= K[1] * P01_temp;

一些建议参数：

float Q_angle = 0.001;
float Q_gyroBias = 0.003;
float R_measure = 0.03;

注意事项：

如果要求滤波器启动时输出有意义，需要给定初试状态；

未完待续。。。。