数据降维LDA，ICA，FA，MFA

书接上文，上文介绍了PCA，接下来介绍几种数据降维的方法。

LDA（Linear Discriminant Analysis, 线性判别分析）

理论推导

线性判别分析是一种有监督的降维方法，核心思想是通过线性变换进行降维，使得不同label下的特征最有区分度
假设有多类数据，类别 $i$ 为 $x\in X_i \Rightarrow y_i$ ，均值 $\mu_i=\frac{1}{|X_i|}\sum_{x\in X_i}x$ ，方差 $\Sigma_i=\frac{1}{|X_i|}\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T$
所有数据总体的均值为 $\mu=\frac{1}{|X|}\sum x$
定义间散度矩阵为 $S_{\mu}=\sum_i \frac{|X_i|}{|X|}(\mu_i-\mu)(\mu_i-\mu)^T$ ，可以看作是不同类别中心点的之间的离散程度
定义内散度矩阵为 $S_{\Sigma}=\sum_i \Sigma_i$ 也有地方定义为 $S_{\Sigma}=\sum_i \frac{|X_i|}{|X|}\Sigma_i$ ，可以看作是不同类别的集中程度

显然我们希望变换后散度矩阵越大越好，内散度矩阵越小越好，要求得线性变换矩阵 $W$ 形式上可以写作

W = a r g m a x_{W} \frac{W^{T} S_{μ} W}{W^{T} S_{Σ} W}

$W=argmax_{W}\frac{W^TS_{\mu}W}{W^TS_{\Sigma}W}$

分子分母都不是数值就很尴尬，我们把他进行变形，令 $W=S_{\Sigma}^{\frac{1}{2}}W$ 可得

W = a r g m a x_{W} \frac{W^{T} S_{μ} S_{Σ}^{- 1} W}{W^{T} W}

$W=argmax_{W}\frac{W^TS_{\mu}S_{\Sigma}^{-1}W}{W^TW}$

分母相当于归一化，等价于令 $W$ 为单位向量，那么上式可以看作是

W = a r g m a x_{W} W^{T} S_{μ} S_{Σ}^{- 1} W + λ (W^{T} W - I)

$W=argmax_{W} W^TS_{\mu}S_{\Sigma}^{-1}W+\lambda(W^TW-I)$

这个式子很熟，在PCA里也见过， $W$ 就是 $S_{\mu}S_{\Sigma}^{-1}$ 前几大的特征值对应的特征向量。

LDA VS PCA

LDA算法的主要优点有：

在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

LDA算法的主要缺点有：

LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
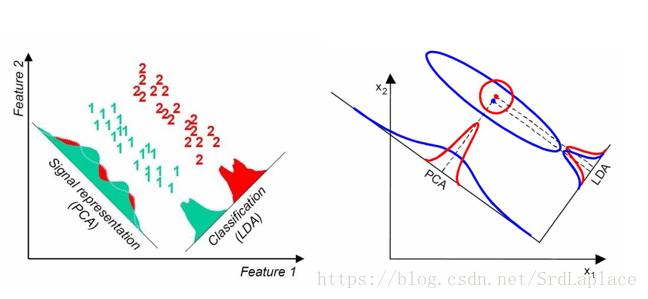
PCA选择保留波动最大的方向，LDA选择保留均值差距最大的方向。

直观示意图：
这里写图片描述

ICA(Independent Component Correlation，独立成分分析)

ICA和前面介绍的PCA和LDA不同的是ICA针对是时序信号，又称盲源分离(Blind source separation, BSS)，假设观察到的随机信号 $x$ 服从模型 $x=As$ ，其中 $s$ 为未知源信号，其分量相互独立， $A$ 为一未知混合矩阵。ICA的目的是通过且仅通过观察 $x$ 来估计混合矩阵A以及源信号 $s$ 。ICA针对是非高斯分布，这点与PCA不同。
大多数ICA的算法需要进行“数据预处理”（data preprocessing）：将 $x$ 白化得到 $z$ ，白化相当于PCA。预处理后得到的z满足下面性质：

z的各个分量不相关；
z的各个分量的方差都为1。

需要注意的是独立意味着不相关，而不相关并不意味着独立。
有许多不同的ICA算法，最大化非高斯指标，例如峰度(Kurtosis，缺点对outlier敏感，鲁棒性不强)、Negentropy(熵 $H(y_{guass})-H(y)$ ， $y_{guass}$ 相同方差情况下的熵，计算复杂度高，需要引入近似值)。这里介绍一种比较简单的方法：
因为 $x=As$ ，那么显然 $s=Wx$ ，可得 $p_x(x)=p_s(Wx)·|W|$
源 $s$ 的联合分布为： $p(s)=\prod_ip(s_i)$
那么 $p_x(x)=\prod p(w_i\cdot x)\cdot |W|$
指定 $s_i$ 的密度，先指定一个累积分布函数 cdf。一个 cdf 是从 0 到 1 的单调递增函数，根据之前的讨论，不能选择高斯累积分布函数，因为ICA在高斯数据上无效。要选择一个合理的能从 0 到 1 缓慢递增的函数，就选择 sigmoid 函数： $g(s)=\frac{1}{1+e^{-s}}$ ，所以 $p(s)=g'(s)$ 。
矩阵 $W$ 是模型的参数，给定训练集 $\{x_i;i=1,...,m\}$ ，log 似然为：

l (W) = \sum_{i} (\sum_{j} l n [g^{'} (w_{i} \cdot x_{i})] + l n | W |)

$l(W)=\sum_i(\sum_jln[g'(w_i\cdot x_i)]+ln|W|)$

梯度下降求 $W=W+α([1-2g(wx)]x_i^T+W^{-T})$
$x_i$ 之间不相互独立的,如果有足够的数据，即使训练集是相关的，也不会影响算法的性能。但是，对于连续训练例子是相关的问题，执行随机梯度下降时，有时碰到一些随机排列的训练集也会加速收敛。

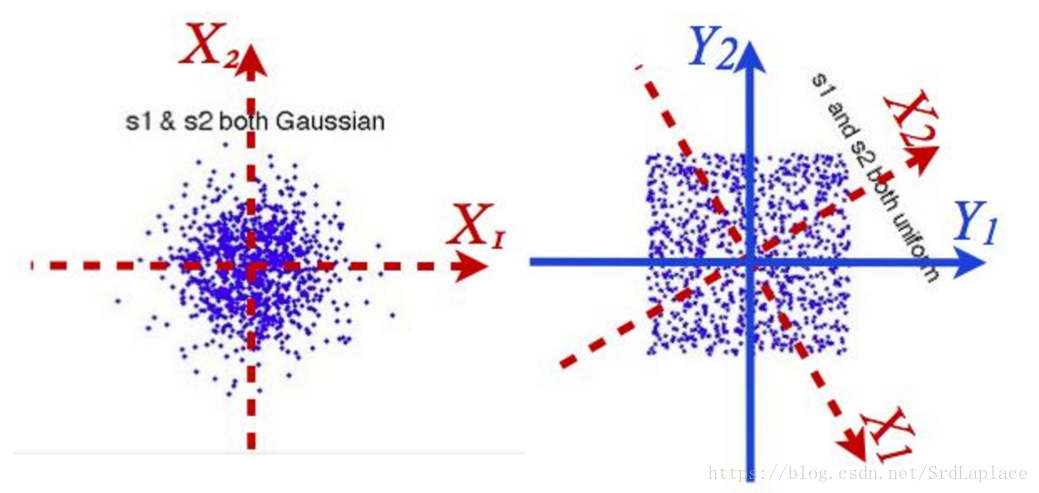
不管是PCA还是ICA，都不需要你对源信号的分布做具体的假设；如果观察到的信号为高斯，那么源信号也为高斯，此时PCA和ICA等价。
给个图就可以看出ICA到底在干啥
这里写图片描述

FA(factor analysis，因子分析)

因子分析的因子都是高斯分布，ICA因子至多一个高斯分布
因子分析的步骤

1.根据研究问题选取原始变量；
2.对原始变量进行标准化并求其相关阵，分析变量之间的相关性；
3.因子分析适合度检验，确定获取的测量数据是否适合于进行因子分析；
4.求解初始公共因子及因子载荷矩阵；
5.因子旋转，通过正交旋转或斜交旋转使得因子模型的意义更加明确；
6.因子得分的计算，以及因子的命名与解释；
7.根据因子得分值进行进一步分析。

$x=\mu +AF+\epsilon$
Optimization: EM算法等
因子都有一定的含义，把原始特征映射到有含义的特征空间，跟PCA有点类似。

MFA(Marginal Fisher Analysis，核技巧的LDA)

训练样本之间的类内紧密性和类间可分性可以采用本征图 $G^+ =\{X, W^+\}$ 和惩罚图 $G=\{X, W\}$ 来分别表示:
$W^+_{ij}=1~if~[i\in N^+_{k_1}(j)~or~j\in N^+_{k_1}(i)]~else~0$
$W_{ij}=1~if~[i\in N_{k_1}(j)~or~j\in N_{k_1}(i)]~else~0$
$N^+_{k_1}(i)$ 表示与样本 $x_i$ 同类的 $k_1$ 个最邻近节点下标集合， $N_{k_2}(i)$ 表示与样本 $x_i$ 异类的 $k_2$ 个最邻近节点下标集合。

与LDA类似，定义类内紧密性：

I n = \sum_{i = 1}^{N} \sum_{i \in N_{k_{1}}^{+} (j) o r j \in N_{k_{1}}^{+} (i)} | | V x_{i} - V x_{j} | |^{2} = \sum_{i = 1}^{N} \sum_{j = 1}^{N} | | V x_{i} - V x_{j} | |^{2} W^{+} = 2 t r (V^{T} X^{T} (D^{+} - W^{+}) X V)

$In=\sum^N_{i=1}\sum_{i\in N^+_{k_1}(j)~or~j\in N^+_{k_1}(i)}||Vx_i-Vx_j||^2=\sum^N_{i=1}\sum^N_{j=1}||Vx_i-Vx_j||^2W^+=2tr(V^TX^T(D^+-W^+)XV)$

Δ I n = X^{T} (D^{+} - W^{+}) X

$\Delta In=X^T(D^+-W^+)X$

$D^+$ 为网络 $W^+$ 的度矩阵（应该能明白啥意思吧。。）

类间紧密性：

I n t e r = \sum_{i = 1}^{N} \sum_{i \in N_{k_{1}} (j) o r j \in N_{k_{1}} (i)} | | V x_{i} - V x_{j} | |^{2} = \sum_{i = 1}^{N} \sum_{j = 1}^{N} | | V x_{i} - V x_{j} | |^{2} W = 2 t r (V^{T} X^{T} (D - W) X V)

$Inter=\sum^N_{i=1}\sum_{i\in N_{k_1}(j)~or~j\in N_{k_1}(i)}||Vx_i-Vx_j||^2=\sum^N_{i=1}\sum^N_{j=1}||Vx_i-Vx_j||^2W=2tr(V^TX^T(D-W)XV)$

Δ I n t e r = X^{T} (D - W) X

$\Delta Inter=X^T(D-W)X$

与LDA一样，求 $V=argmax_V\frac{Inter}{In}$ ， $V$ 为 $\Delta In \Delta Inter^{-1}$ 最大的前几个特征值对应的特征向量。