以下内容笔记出自‘跟着迪哥学python数据分析与机器学习实战’,外加个人整理添加,仅供个人复习使用。
若数据集特征十分庞大,可能会使计算任务变得繁重,在数据特征有问题时,可能会对结果造成不利影响。
因此可以用降维算法,通过某种映射方法,将原始高维空间中的数据点映射到低纬度的空间中。这里介绍LDA(有监督学习算法)。
线性判别分析(Linear Discriminant Analysis,LDA),也叫作Fisher线性判别,最开始用于分类任务,但由于其对数据特征进行了降维投影,成为一种经典的降维方法。
降维原理
降维任务是找到合适的投影方向,使得原始数据更容易被计算机理解并利用。
实例说明如下:
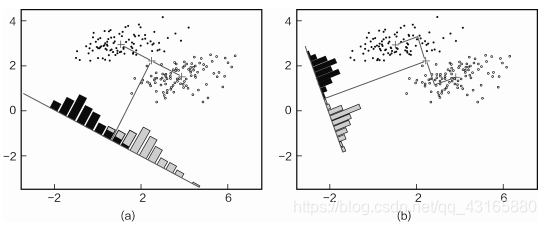
如上图,正,散点是原始数据,即原始数据是二维特征,现在想降到一维,就需要找一个合适的投影方向,把这些数据点全部映射过去。
(a)图中,数据点投影后,有一部分还是重合的,(b)图中,投影后数据点能够明显区别开,那么我们会选第二种降维方式。
由此可见,降维不仅要压缩数据特征,还要寻找最合适的方向,使得压缩后的数据更有利用价值。
我们的目标:
- 对于不同类别的数据点,希望经过投影后的能离得越远越好,区别地越开越好;
- 对于同类别的数据点,希望投影后能更集中,离组织的中心越近越好。
接下来围绕上面的目标进行。
优化目标
如何衡量不同类别数据点投影后越远越好
用矩阵变换表示数据操作,将数据映射到合适的方向上,就是投影。
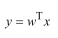
x表示原始数据所在空间,y表示降维后数据,目标就是求解最合适的参数W,这些参数能够保证一个最合适的投影方向。
要使得距离越远越好,我们用数据点均值表示中心位置,不同类别的中心点距离表示类别间距离。
中心点计算:
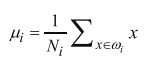
投影后中心点计算:
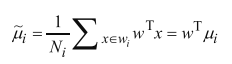
(因此LDA是有监督问题,需要知道类别标签,才能计算类别中心点)
不同类别的中间点距离计算:
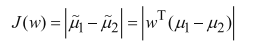
函数J(w) 越大,表示类别间区分的越开。
如何衡量相同类别投影后越集中越好
上面我们得到了不同类别距离的计算,但如果只将上一项作为目标是否可行呢?
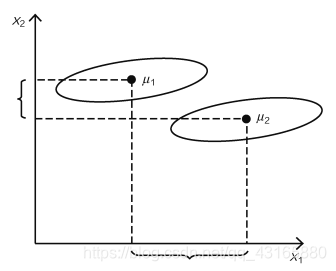
看图说话,上图两类数据点,假设现有两个投影方向,分别为X1,X2.
可以看到,在X1投影方向上,投影后不同类别中心点的距离要大于X2投影方向,X1投影方向的J(w)表现更好。
但X1上,投影后两类数据点依旧有很多重合在一起,但X2投影方向上,投影后数据重合比较好,这个层面上,X2的投影方向更优。
因此就涉及到第二个优化目标,同类别数据点越集中越好。
可以使用另一个度量指标——散列值(scatter)宝石同类别数据点的离散程度:
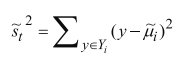
其中,y表示投影后数据点,散列值表示密集程度,值越大,越分散。(类似于方差的含义)。
判别分析求解
将上文中提到的两个目标整合:
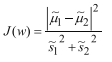
上式中,分子表不同类别数据投影后距离,越大越好;分母表示同类别数据投影后密集程度,越小越好,最终J(w)值越大越好,求解其极大值即可。
化简
首先分母部分:
将散列值(求方差)的式子化简:
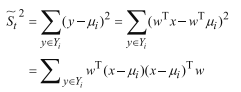
令:
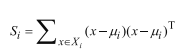
类内散布矩阵:
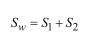
那么有:
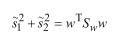
然后分子部分:
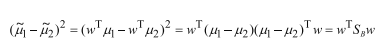
其中,Sb为类间散布矩阵。
最终目标函数:
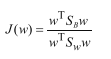
对于散列矩阵Sb和Sw,只要有数据和标签即可求解,但如何得最终结果?若同时求解,就会有无数多解,通用方案是先固定分母,经放缩变换后,限定为1,即:
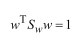
在这个条件下,用拉格朗日乘子法求解分子:
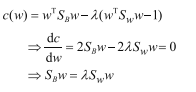
目标是求解w,上式左右两边同时乘以Sw的逆矩阵:
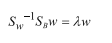
观察上式,与线代里面求特征向量有点像,如果把左式的
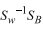
部分作为整体,那么w就是其特征向量。
因此,线性判别分析求解的过程,就是得到类内和类间散布矩阵,然后求其特征向量,就可以得到投影方向了!