目录
1 PCA/LDA
参考我的这篇博文 主成分分析(PCA)/线性判别分析(LDA)总结
2 Factor Analysis
FA 的思想与 PCA 其实很相似,假设高维度上的观测结果 X 其实是由低维 度上的 factors 来支配的。打个比方,笔者身边有一大群妹子,每个妹子都有很多的参数,例 如,身高,体重,肺活量,皮肤,眼睛大小,脸蛋形状,发型,性格等 8 个参数... 笔者经过大 量的调查研究把每个妹子在每个 feature 上都打了从 1到10 的分数(10 分最高),然后就在纠 结,到底要对哪个下手呢?于是就想把妹子们做个 ranking,但是只能 rank 一维的数据呀,于 是就在想能不能把妹子的 8 个 feature 抽象成一个终极打分 美貌。于是做了如下的假设:
假设每个妹子都有一个终极打分 z(一维),这个分数将会通过一个固定的映射到八个维度 上,然后加上 bias 修正,再加上一些误差(误差保证尽管俩妹子得分一样,也可以春兰秋菊 各有千秋),于是就得到了八维打分 X。这个过程的原理可以让下面这俩图来解释一下: 首先强行把一维的数据搬到二维平面的一条直线上,再加上噪声,bias,于是就 得到了红圈里的一个二维的数据,把二维想象成八维就重构了妹子们的参数。

有了这个模型,我们就可以就用 EM(expectationmaxminization) 来估算 , 估算过程比较复杂,一句话讲就是通过调整这些参数,令 P(X) 出现的概率最大。 模型确定下来,就可以算出妹子们的最终得分 z, 排个序, 就可以从容地选择了! 继续看下蛋卷图
原图:
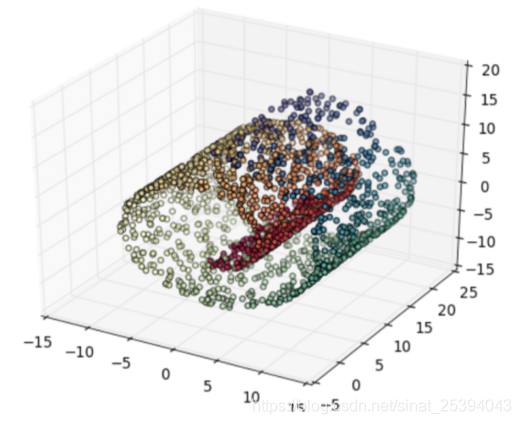
降维后的:
线性的算法基本就是这个样子,可以看到线性的算法能把最重要的维度们找出来,蛋卷的形状被保全了下来, 但是对很多应用场景来说线性的算法然并卵, 因为如果原来的数据线性不可分降维了之后还是不可分。于是就需要这些 nonlinear 的算法, 其实这些非线性算法像 LLE, Laplacian EM 都属于流形学习 (manifold learning)。何为流形呢? 笔者的理解就是尽管一个模型很复杂很nonlinear, 但是它的一个很小的局部还是可以近似成一个线性模型的。比如说, 地球是三维的,是个球, 但是在我们渺小的人类视野所及之内地球是平的, 是个 2D 平面, 我们也可以把地图做成二维平面的样子, 然后由一张张二维地图线性地拼接成世界地图。
3 LLE
Locally linear embedding 局部线性嵌入
LLE 可以说是流形学习里面最有代表性的一个算法, 最早由 NYU 的 Sam Roweis 教授发表在 Science 上,到现在已经有快 1 万的引用了, 可见 LLE 这个算法是多么的有影响力
LLE 的主要思想着眼于流形局部的结构,对每一个样本点 x,找出它的 topk 最近邻居,然后把 x 用邻居们线性表示。然后尝试到低维空间构造 y ,令 y 可以被邻居们用同样的线性规则表示。这样以来,高维里面的流形结构到了低维里面仍然会被保留下来。按照这个思想,LLE 由三个主要步骤组成:
- 找邻居:对于每一个样本 ,找到 topk 最近邻(欧式距离)
- 找到重构系数:用邻居们重构 并且最小化重构误差,用类似这样的优化问题
- 找低维点:令他们相互之间都可以用上个步骤计算出来的系数线性表示,用类似这样的优化问题
LLE 的思想就是这样,值得注意的是找低维点的那个优化问题最后又变成了 SVD 问题(SVD 真的是无处不在,而且真的非常重要,后面还会经常见到)。经过 LLE 打击后的蛋卷长这样:

与上两个蛋卷相比, LLE 蛋卷像是展开,那俩蛋卷像是压扁,这时候本来线型不可分的点变成了线型可分。
原理可参考这篇文章 局部线性嵌入(LLE)原理总结
4 LEP
拉普拉斯特征映射(Laplacian Eigenmaps)
参考这篇文章降维算法总结比较(二)中对于LEP的讲解
