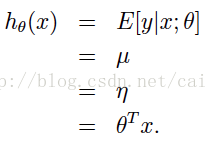菜鸟学习记003 ---------机器学习--------GLM广义线性模型

本文为学习笔记，供自己复习回顾，分享，交流，如果专家们发现谬误之处欢迎批评与修正。

----------------------------------------------------------------------------------------------------------------------------

1.什么是线性模型？

在数学中，变量间关系有两种基本类型：函数关系和相关关系，函数关系是确定的可以用函数式表达出来的。

因此，线性模型就是一个响应变量（因变量）与其解释变量（因变量）的线性组合存在线性关系的模型。

1.1 基本形式

给定由  个属性描述的示例,其中 是  在第  个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

                                              

其中  是属性权重， 是偏移项， 是误差项，一般情况下偏移项与误差项统一处理， 与  学得后，模型就可以确定了。

1.2 如何判别线性模型

我们很多情况认为直线就是线性模型，其实有些曲线也是线性模型，我刚接触这个概念时，一直很不解为什么逻辑模型是线性模型，所以在这里列出两条判断线性模型的标准方法。

1. 自变量前是否只有一个系数影响

e.g.  逻辑回归其分离面是一个线性超平面wx+b,  本质上是一个线性回归模型，其系数是线性函数，只是在其基础上加入了sigmoid映射，没有加入前其形式为

                                                               

加入后

                                                             

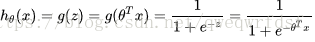
所以逻辑回归实质是一个线性模型。

2. 自变量前是否只有一个系数影响

 e.g.                     

  

虽然画出来是曲线关系，但是它是一个线性模型因为x1*w1 中可以观察到 x1只被一个w1影响。

这个模型就不是线性模型，因为x1不仅仅被参数w1影响，还被w5影响，如果自变量被两个以上参数影响，那么就是非线性。

1.3 条件假设

普通线性模型的假设条件有以下几点：

1. Y与  正态性： Y 与   服从正态分布，并且   具有零均值，同方差的特性。

2. 自变量X和其参数 W 非随机性：自变量具有非随机性，可测且不存在测量误差，参数W认为是未知但不具有随机性的常数，值得注意的是，运用最小二乘或者极大似然解出参数W的估计值具有正态性。

3. 研究对象，普通线性模型主要研究相应变量的均值 E[Y].

4. 联接方式， 在上面三点假设下，对基本公式两边取数学期望，可得

                       

因此，在普通线性模型中，响应变量的均值  与 描述变量的线性组合通过恒等式联接，也可以认为是通过形如的联接函数（link function）进行联接，即

     

1.4 特点

线性模型形式简单，易于建模，但却蕴含着机器学习中一些重要的基本思想，并且由于W直观表达了个属性的权重重要性，所以线性模型有很好的解释性。

但线性回归并不适用于所有情况，很多相应变量并不能简单地被变量线性组合解释，例如我们最熟悉的二分类问题采用的逻辑回归，所以我们扩展了简单线性模型为广义线性模型用来解决更多的问题，其实逻辑回归也是一种广义线性模型。

2.GLM 广义线性模型

2.1 指数分布族

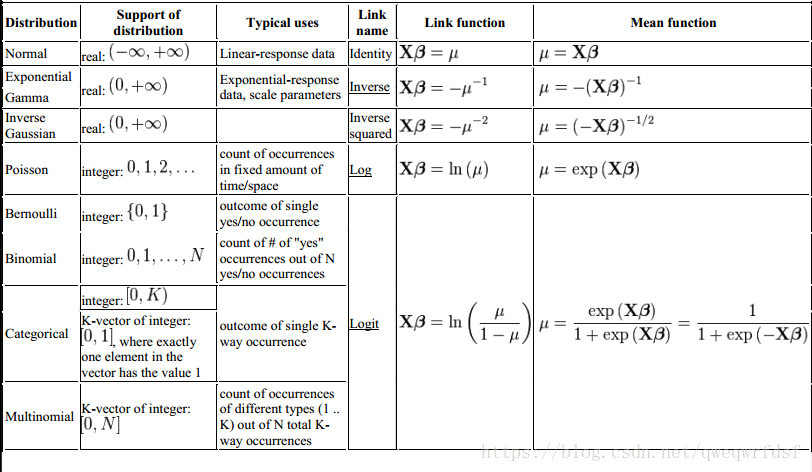
介绍GLM前，我们需要先了解指数分布族，大多数或者可以说我们接触的GLM都是服从指数分布族的，因为我们所见到的高斯分布，伯努利分布，泊松分布等等都是属于指数分布族的。

2.1.1 基本形式

服从指数分布族的条件是概率分布可以写成如下形式（注：不是概率密度函数，因为不同教材采用的不一样）：

                                                

: 底层观测值

 ：自然参数，指数分布族唯一参数，通常为一个实数

: 充分统计量，很多情况下 被称作 log partition function

: 配分函数

 本质上在归一化常数发挥了作用， 确保了   分布 关于  的和或积分 是 1.

固定的T , a,  b 函数定义了一个以  自以为ucabs关于的分布族，当改变  时，得到族内的不同分布。

2.1.2 常见分布推导

为了加深理解和认识，这里会推导出几种常见分布的指数分布形式。

1.伯努利分布

伯努利分布是对0，1分布的问题进行建模，对于, ,其概率密度函数如下，

                                                               

因此，

                                                          

                                                                           

                                                                           

其中：

                                                          

                                                          

                                                          

                                                          

2.高斯分布（正态分布）

方差没影响，所以为了方便起见将方差设为1，因此过程如下：

                                             

                                                               

其中：

                                             

                                             

                                             

                                             

2.2 假设条件

说是假设，其实更应该是设计广义线性模型的条件，下面由三个条件：

1.响应变量基于解释变量的条件概率分布服从指数分布族，即：

2. 对于给定的输入变量X，学习的目标是预测的期望值，其实，经常就是

3.和输入变量X的关联是线性的，即: 

e.g. 线性回归的条件概率分布是正态分布，为指数分布族； 我们的目的是预测 的期望，由上述高斯推导知道，，而  的期望值也就是正太分布参数  ，由上述可知，，而且，所以线性回归为广义线性回归的一个特例。

其模型为:

                                                                               

2.3 组成成分

GLM广义线性模型由三部分组成：

1. 随机部分（Random Component）

响应变量及其概率分布，服从指数族。

e.g.

当处理连续值时，服从正态分布，使用简单线性回归。

当处理服从二项分布的输出二分类的时候，使用逻辑回归。

当处理随机事件次数的时候，服从泊松分布，使用泊松回归。

2.系统部分 （Systermatic Component）

是一个线性模型形如：

                                

3.联接部分 （Link Component）

联接函数  用来联接 随机部分和系统部分，即：

                                                        

                           

注：联接函数是单调可导的。

常见分布的经典应用以及联接函数如下：

2.4 怎样使用广义线性模型

下面的流程图已经很好的解释了什么情况下如何使用GLM：

参考：1.周志华《机器学习》