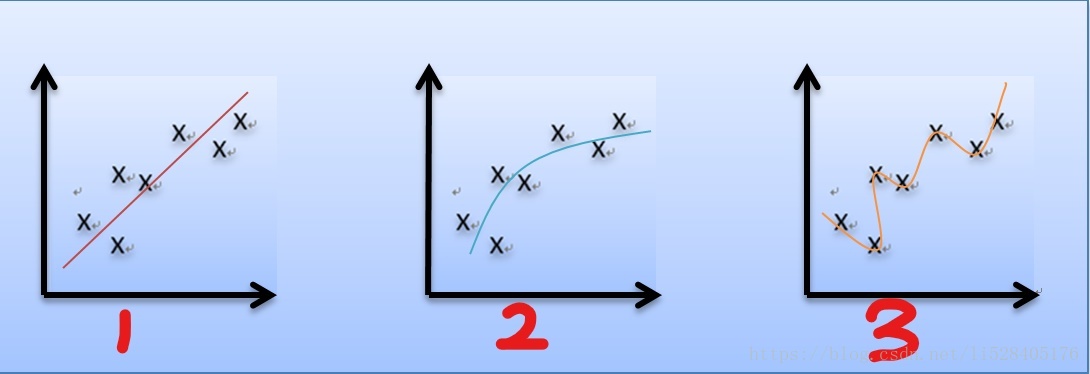
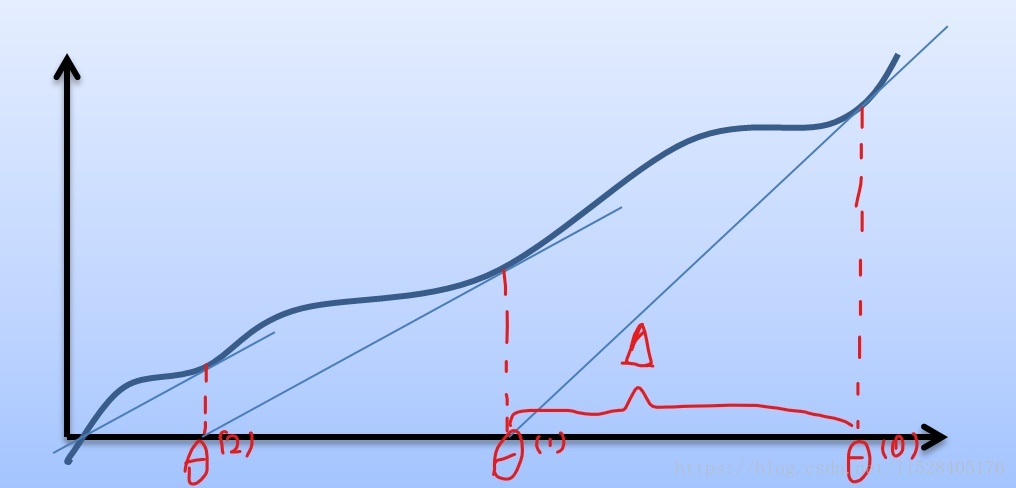
机器学习cs229——（三）局部加权回归、逻辑回归、感知器、牛顿方法、广义线性模型

首先，我们先来讨论一下欠拟合（underfitting）和过拟合（overfitting）问题。比如我们同样采用线性回归来对一组房屋价格和房屋大小的数据进行拟合，第一种情况下我们只选取一个数据特征(比如房屋大小 x)采用直线进行拟合。第二种情况下选取两个数据特征(比如房屋大小 x ,以及房屋大小的平方 $\small x^{2}$ )采用二次函数拟合。第三种情况由于只有七个数据样本所以最多只能选取六个数据特征(x、 $\small x^{2}$ ... )进行最高6次多项式的拟合。拟合效果如下图：

如图1所示，由于选取的特征太少，使得数据偏离曲线较远，拟合的效果并不能很好的体现数据的变化趋势，我们称之为欠拟合。而如图3所示，另一种情况下由于选取的特征过多，使得拟合所得曲线虽然精确的穿过了每一个数据样本，但却仅仅反映了所给的特定数据的特点，而不是隐藏在其中的房屋价格随房屋大小变换的一般规律。这种情况我们称之为过拟合。

参数学习算法（Parametric learning algorithm）

是指一类有固定数量的参数以进行数据拟合的算法。

非参数学习算法（Non-parametric learning algorithm）

是指参数数量会随着训练集合的大小线性增长的算法。即算法的每次运行是基于整个训练集合的，即使在训练学习之后。局部加权回归就是一个非参数学习算法。

局部加权回归（Locally weighted regression）

由于历史原因，也被称为 Loess/lowess 。这个算法可以让我们不用担心特征的选择。算法的模型不是固定的，且参数大小不是固定的，而是根据训练样本点与预测点的距离建立起临时模型。每次预测都需要重新计算一组参数值并建立新的临时模型，因此计算代价很大，不适合大规模的数据集。

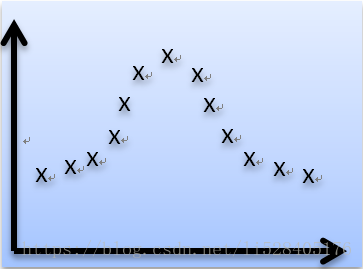
例如，对下图的数据集做局部加权线性回归：

对于局部加权线性回归，我们为每一个样本数据的预测损失添加一个权值，然后对加权后的损失值求和得到样本集合总的预测代价。然后调整参数向量 $\small \Theta$ 使得代价最小：

即最小化下式

$\tiny \sum_{i}\omega ^{\left ( i \right )}\left ( y^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}$

其中， $\small \omega ^{\left ( i \right )}$ 表示训练集合中第 i 个数据在拟合过程中所占的权值，即贡献度。定义如下：

$\tiny \sum_{i}\omega ^{\left ( i \right )}=e^{-\frac{\left ( x^{\left ( i \right )} -x\right )^{2}}{2\tau^{2} }}$

其中 $\small \tau$ 称为波长参数，它控制着权值随距离变化的速率。 越大远距离样本的权值下降更快。

观察权值函数形式易得，样本数据越靠近待预测点权值越大(接近于1)，相反样本数据越远离待预测点权值越小(接近于0)，相当于在待预测点邻域内构成局部线性回归。如下图

需要注意，局部加权回归并不能避免欠拟合和过拟合的问题，关键就在于设置的波长参数是否合适。

对于线性回归算法，一旦拟合出适合训练数据的参数向量 $\small \Theta$ ，就保存这些参数，对于之后的预测，不需要再使用原始训练数据集，所以是参数学习算法。

对于局部加权线性回归算法，每次进行预测都需要全部的训练数据（每次进行的预测得到不同的参数向量 $\small \Theta$ ），没有固定的参数，所以是非参数算法。

线性回归的概率解释

利用高斯概率分布（即正态分布）进行推导，最终可以得出线性回归代价函数采用最小二乘形式的原因。

假设：

$\tiny y^{\left ( i \right )}=\Theta ^{T}x^{\left ( i \right )}+\varepsilon ^{\left ( i \right )}$

其中， $\small \varepsilon ^{\left ( i \right )}$ 为误差项，它是对未利用的其他特征的补充(比如房子有没有花园、壁炉之类的特征)或者将其看成随机噪声(比如卖家当天的心情等)，总之误差项捕获了未建模的效应。

假设误差项服从正态分布： $\tiny \varepsilon ^{\left ( i \right )}\sim N\left ( 0,\sigma ^{2} \right )$ 即：

$\tiny P\left ( \varepsilon ^{\left ( i \right )}\right )=\frac{1}{\sqrt{2\pi }\sigma } e^{\left ( -\frac{\left ( \varepsilon ^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}} \right )}$

这意味着在给定样本特征 x 和参数 $\small \Theta$ 时房价也服从高斯分布，其概率密度函数：

$\tiny P\left ( y^{\left ( i \right )}|x^{\left ( i \right )};\Theta \right )=\frac{1}{\sqrt{2\pi }\sigma } e^{\left ( -\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}} \right )}$

即给定样本值和参数

$\tiny y^{\left ( i \right )}\sim N\left ( \Theta ^{T} x^{\left ( i \right )},\sigma ^{2}\right )$

再假设 $\small \varepsilon ^{\left ( i \right )}$ 之间满足独立同分布

则参数 $\small \Theta$ 的极大似然函数为：

$\tiny L\left ( \Theta \right )= \prod_{i=1}^{m}P\left ( y^{\left ( i \right )}|x^{\left ( i \right )};\Theta \right )=\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi }\sigma }e^{\left ( -\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}} \right )}$

对数似然函数：

$\tiny \dpi{300} \tiny l\left ( \Theta \right )= logL\left ( \Theta \right )= log\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi }\sigma }e^{\left ( -\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}} \right )}$

$\tiny =\sum_{i=1}^{m}log\left [ \frac{1}{\sqrt{2\pi }\sigma }e^{\left ( -\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}} \right )} \right ]$

$\tiny =mlog\frac{1}{\sqrt{2\pi }\sigma }-\sum_{i=1}^{m}\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}}$

最大化似然函数，相当于最小化

$\tiny \sum_{i=1}^{m}\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2\sigma ^{2}}$

其中 $\small \sigma$ 为常数，因此可忽略，即最小化

$\tiny \sum_{i=1}^{m}\frac{\left ( y ^{\left ( i \right )}-\Theta ^{T}x^{\left ( i \right )} \right )^{2}}{2}=J\left ( \Theta \right )$

参考：https://blog.csdn.net/shaohuacheng/article/details/51985944

https://blog.csdn.net/sz464759898/article/details/43957433?utm_source=blogxgwz0

分类

之前介绍过的回归算法中，我们预测的连续变量，其取值可以是任意的。分类算法中，我们预测的变量 y 是离散的，一般情况下限定 y 只能取给定的几个值。

这里我们先来介绍二分类问题 $\small y\in \left \{ 0,1 \right \}$

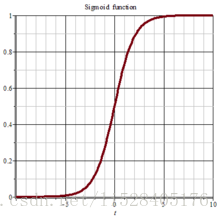
由此我们需要假设一个预测函数 $\small h_{\Theta }\left ( x \right )\in \left [ 0,1 \right ]$

多数情况下，我们会选择利用Sigmoid函数将 $\small h_{\Theta }$ 映射到[0,1]区间上。Sigmoid函数也称作logistic函数，形式如下：

$\large S\left ( x \right )= \frac{1}{1+e^{-x}}$

函数图形为

于是

$\tiny h_{\Theta }\left ( x \right )=S\left ( \Theta ^{T}x \right )= \frac{1}{1+e^{-\Theta ^{T}x}}$

预测时，当 $\small h_{\Theta }\left ( x \right )$ 小于等于0.5时，结果是0，如果 $\small h_{\Theta }\left ( x \right )$ 大于0.5时，结果是1。

下面进行概率意义上的解释

假设：

对于给定的以 $\small \Theta$ 为参数的 $\small x$ ， y=1 的概率为： $\small P\left ( y=1|x;\Theta \right )=h_{\Theta }\left ( x \right )$

对于给定的以 $\small \Theta$ 为参数的 $\small x$ ， y=0 的概率为： $\small P\left ( y=0|x;\Theta \right )=1-h_{\Theta }\left ( x \right )$

合并以上两式：

$\tiny P\left ( y|x;\Theta \right )=h_{\Theta }\left ( x \right )^{y}(1-h_{\Theta }\left ( x \right ))^{1-y}$

然后利用最大似然估计来求参数 $\small \Theta$ 。所谓最大似然估计：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

参数的似然性：

$\tiny L\left ( \Theta \right )= \prod_{i}P\left ( y^{\left ( i \right )}|x^{\left ( i \right )};\Theta \right )=\prod_{i}h_{\Theta }\left ( x^{\left ( i \right )} \right )^{y^{\left ( i \right )}}(1-h_{\Theta }\left ( x^{\left ( i \right )} \right ))^{1-y^{\left ( i \right )}}$

通常来讲，使参数的似然性最大化很难。但是使参数似然性的对数最大化要相对简单，并且对数能够保证样本原来的单调性。于是求似然性对数：

$\tiny l\left ( \Theta \right )= logL\left ( \Theta \right )= \sum_{i=1}^{m}\left [ y^{\left ( i \right )}log h_{\Theta }\left ( x^{\left ( i \right )} \right )+\left ( 1-y^{\left ( i \right )} \right )log\left ( 1-h_{\Theta }\left ( x^{\left ( i \right )} \right ) \right ) \right ]$

对于线性回归问题当中我们使用梯度下降(减去梯度的 $\small \alpha$ 倍)算法最小化代价函数，这里我们可以使用梯度上升(加上梯度的 $\small \alpha$ 倍)算法来最大化似然函数。参数 $\small \Theta$ 通过下式更新：

$\tiny \Theta = \Theta +\alpha \triangledown _{\Theta }l\left ( \Theta \right )$

其中经过简单计算可知

$\tiny \triangledown _{\Theta }l\left ( \Theta \right )= \frac{\partial }{\partial \Theta _{j}}l\left ( \Theta \right )= \sum_{i=1}^{m}\left ( y^{\left ( i \right )}-h_{\Theta }\left ( x^{\left ( i \right )} \right ) \right )x_{j}^{\left ( i \right )}$

所以推得

$\tiny \Theta _{j}=\Theta _{j}+\alpha \sum_{i=1}^{m}\left ( y^{\left ( i \right )}-h_{\Theta }\left ( x^{\left ( i \right )} \right ) \right )x_{j}^{\left ( i \right )}$

形式上类似于上一篇中最小二乘回归的梯度下降解法（https://mp.csdn.net/postedit/83015509）。但其实二者并不相同，因为两个式子中的 $\small h_{\Theta }\left ( x \right )$ 的定义不同。这里的函数并不是之前的线性函数，而是关于 $\small \Theta^{T}x$ 的logistic函数。

感知器

不同于逻辑回归，感知器算法的分类规则为：

$\tiny g\left ( z \right )= \left\{\begin{matrix} 1 & z \geqslant 0\\ 0& else \end{matrix}\right.$

于是预测函数定义为：

$\tiny h_{\Theta }\left ( x \right )=g\left ( \Theta ^{T}x \right )$

经过与逻辑回归部分相同的推导步骤，可得参数的批梯度更新公式：

$\tiny \Theta _{j}=\Theta _{j}+\alpha \sum_{i=1}^{m}\left ( y^{\left ( i \right )}-h_{\Theta }\left ( x^{\left ( i \right )} \right ) \right )x_{j}^{\left ( i \right )}$

由于其生成的值只有0和1，所以很难赋予其概率意义上的解释。

牛顿方法

牛顿方法对于逻辑回归效果很好，对广义线性模型来说效果也不错。

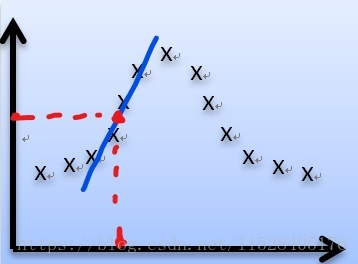
问题：给定一个函数 f( $\small \Theta$ ) ,找到其零点。

如上图所示，首先我们用某个值(通常为0)初始化 $\small \Theta$ ，记做 $\small \Theta ^{\left ( 0 \right )}$ 。然后求出该点的切线，与横轴交于一点，记做 $\small \Theta ^{\left ( 1 \right )}$ ，即完成一次迭代。然后按照同样的方法求出 $\small \Theta ^{\left ( 1 \right )}$ 处的切线，与横轴交于 $\small \Theta ^{\left ( 2 \right )}$ 点，完成第二次迭代。以此类推，最终将逼近函数零点。

根据斜率求 $\small \Delta$ ：

$\tiny f^{'}\left ( \Theta ^{\left ( 0 \right )} \right )=\frac{f\left ( \Theta ^{\left ( 0 \right )} \right )}{\Delta} \Rightarrow \Delta = \frac{f\left ( \Theta ^{\left ( 0 \right )} \right )}{f^{'}\left ( \Theta ^{\left ( 0 \right )} \right )}$

然后计算下个次迭代的切点：

$\tiny \Theta ^{\left ( 1 \right )}=\Theta ^{\left ( 0 \right )}-\Delta =\Theta ^{\left ( 0 \right )}- \frac{f\left ( \Theta ^{\left ( 0 \right )} \right )}{f^{'}\left ( \Theta ^{\left ( 0 \right )} \right )}$

易推得 $\small \Theta$ 迭代公式：

$\tiny \Theta ^{\left ( t+1 \right )}=\Theta ^{\left ( t \right )}- \frac{f\left ( \Theta ^{\left ( t \right )} \right )}{f^{'}\left ( \Theta ^{\left ( t \right )} \right )}$

比如我们想要使得对数似然函数 $\small l\left ( \Theta \right )$ 取得最大值，可以令其导数等于0（log函数单调），即 $\small l^{'}\left ( \Theta \right )= 0$ 。

于是可得迭代公式为：

$\tiny \Theta ^{\left ( t+1 \right )}=\Theta ^{\left ( t \right )}-\frac{l^{'}\left ( \Theta ^{\left ( t \right )} \right )}{l^{''}\left ( \Theta ^{\left ( t \right )} \right )}$

牛顿方法是一个收敛速度非常快的算法，其收敛速度为二次收敛。在一般化的牛顿方法中， $\small \Theta$ 是一个向量，迭代公式为：

$\tiny \Theta ^{\left ( t+1 \right )}=\Theta ^{\left ( t \right )}-H^{-1}\triangledown _{\Theta }l$

其中，H 是Hession矩阵

$\tiny H_{ij}= \frac{\partial ^{2}l}{\partial\Theta _{i}\partial \Theta _{j} }$

与梯度上升算法比起来，牛顿方法所需要的迭代次数要少得多。但其缺点是，每一次迭代都需要重新计算 Hession 矩阵的逆。Hession 矩阵是一个 n*n 的矩阵，n 为特征的数量，因此如果要处理具有大量特征的问题，矩阵的逆运算会消耗大量的计算资源。所以牛顿方法只适用于特征较少的问题。

广义线性模型（Generalized Linear Model）

前面我们介绍了两种算法对 $\small P\left ( y|x;\Theta \right )$ 进行建模：

当 $\small y\in \mathbb{R}$ ，我们假设 y 满足Gaussion分布 $\small \rightarrow$ 基于最小二乘法的线性回归

当 $\small y\in \left \{ 0,1 \right \}$ ，只有两个取值的随机变量满足Bernoulli分布 $\small \rightarrow$ logistic回归

事实上，这两种算法都属于广义线性模型的特例。

伯努利分布 Bernoulli( $\small \Phi$ ) 即 P(y=1; $\small \Phi$ )= $\small \Phi$ 同理看高斯分布 $\small N\left ( \mu ,\sigma ^{2} \right )$

这两类分布都属于指数分布族的特例。

如果一个概率分布可以写成下面的形式

$\tiny {\color{Magenta} P\left ( y;\eta \right )=b\left ( y \right )e^{\eta ^{T}T\left ( y \right )-a\left ( \eta \right )}}$

则称为指数分布族。

其中， $\small \eta$ 被称为分布的自然参数。T(y) 被称为充分统计量（对于未知参数的估计问题,保留了原始样本中关于未知参数θ的全部信息的统计量,就是充分统计量。通常T(y)=y ）

只要我们固定了a、b 和 T 三个函数，指数分布族的公式就定义了一个以 $\small \eta$ 为参数(通常为标量)的概率分布的集合（即定义了一类概率分布，对于固定的a、b 和 T，只要改变 $\small \eta$ 就可以得到一个不同的概率分布）。例如：

对于伯努利分布

$\tiny \dpi{300} \tiny P\left ( y;\Phi \right )=\Phi ^{y}\left ( 1-\Phi \right )^{\left ( 1-y \right )}= e^{\left ( log\Phi ^{y}\left ( 1-\Phi \right )^{\left ( 1-y \right )} \right )}$

$\tiny = e^{\left ( ylog\Phi +\left ( 1-y \right )log\left ( 1-\Phi \right ) \right )}$

$\tiny = e^{\left ( ylog\frac{\Phi }{1-\Phi } +log\left ( 1-\Phi \right )\right )}$

即 $\tiny \eta = log\frac{\Phi }{1-\Phi }$ ， $\tiny {\color{Red} T\left ( y \right )=y}$ ， $\tiny -a\left ( \eta \right )=log\left ( 1-\Phi \right )$ ， $\tiny {\color{Red} b\left ( y \right )=1}$

由 $\tiny \eta = log\frac{\Phi }{1-\Phi }$ 推得 $\tiny \Phi = \frac{1}{1+e^{-\eta }}$

将 $\tiny \Phi = \frac{1}{1+e^{-\eta }}$ 代入 $\tiny -a\left ( \eta \right )=log\left ( 1-\Phi \right )$ 可得 $\tiny {\color{Red} a\left ( \eta \right )=log\left ( 1+e^{\eta } \right )}$

对于高斯分布

$\tiny N\left ( \mu ,\sigma ^{2} \right )$ ，由于 $\small \sigma$ 对参数无影响，这里将其设置为 $\tiny \sigma ^{2}=1$ ,推导可得

$\tiny \frac{1}{\sqrt{2\pi }}e^{\left ( -\frac{1}{2}\left ( y-\mu \right ) ^{2}\right )}=\cdots = \frac{1}{\sqrt{2\pi }}e^{\left ( -\frac{1}{2} y ^{2}\right )}e^{\left ( \mu y-\frac{1}{2}\mu ^{2} \right )}$

即 $\tiny \eta = \mu$ ， $\tiny {\color{Red} T\left ( y \right )=y}$ ， $\tiny {\color{Red} a\left ( \eta \right )=\frac{1}{2}\mu ^{2}=\frac{1}{2}\eta ^{2}}$ ， $\tiny {\color{Red} b\left ( y \right )= \frac{1}{\sqrt{2\pi }} e^{ -\frac{1}{2}y^{2} }}$

实际上大部分常见的概率分布都可以写成指数分布族的形式，比如高斯分布、多元正态分布、伯努利分布(2个结果的事件)、多项式分布(k个结果的事件)、泊松分布(对计数过程进行建模，如网站的访客数量、商店的顾客数量)、伽马分布和指数分布(这两种考虑的是正数的分布，常用来对时间间隔进行建模，比如公车站下一辆车什么时候到)、 $\small \beta$ 分布和Dirichlet分布(这两种是用来对小数进行建模的，是对概率分布进行建模的概率分布)、Wishart分布(协方差矩阵的分布)等等都可以写成指数分布族的形式。

下面考虑选定了指数分布族，怎么用它来推导出一个广义线性模型？

1、假设 $\small P\left ( y|x;\Theta \right )$ 属于以 $\small \eta$ 为参数的指数分布族。我们可以选取 a、b、T 使得 y 在给定的以 $\small \Theta$ 为参数的 x 下的概率分布属于以 $\small \eta$ 为参数的指数分布族（即根据问题选定概率分布模型并推导其指数分布族）。

2、假设参数 $\small \eta$ 与输入特征之间的关系是线性的，即 $\tiny {\color{Blue} \eta = \Theta ^{T}x}$

3、计算 T(y) 在给定 x 下的期望作为该指数分布族的广义线性模型 $\small h_{\Theta }\left ( x \right )$ ，即 $\tiny {\color{Blue} h_{\Theta }\left ( x \right )=E\left [ T\left ( y \right )|x \right ]}$ 。

例如对于伯努利分布

$\tiny h_{\Theta }\left ( x \right )=E[y|x;\Theta ]=P\left ( y=1|x;\Theta \right )=\Phi$

$\tiny =\frac{1}{1+e^{-\eta }}$

$\tiny =\frac{1}{1+e^{-\Theta ^{T}x }}$

刚好得到的是逻辑回归模型。

介绍两个术语： $\tiny g\left ( \eta \right )=E\left [ y;\eta \right ]=\frac{1}{1+e^{-\eta }}$ 称作正则响应函数， $\tiny g^{-1}\left ( \eta \right )$ 称为正则关联函数

广义线性模型中最复杂的例子是多项式分布(多分类问题)

假设一共有 k 类，概率分别为 $\small \Phi _{1}$ 、 $\small \Phi _{2}$ 、 $\small \cdots$ 、 $\small \Phi _{k}$ 即

$\small P\left ( y=i \right )=\Phi _{i}$

由于 $\small \small \Phi _{1}+\small \Phi _{2}+\cdots +\small \Phi _{k}=1$ ，可以推得 $\small \Phi _{k}=1-(\Phi _{1}+\small \Phi _{2}+\cdots +\small \Phi _{k-1})$

因此以 $\small \Phi _{1}$ 、 $\small \Phi _{2}$ 、 $\small \cdots$ 、 $\small \Phi _{k}$ 作为参数对于多项式分布来说其实是冗余的，结果被过度参数化了。所以我们将多项式分布的参数设为： $\small \Phi _{1}$ 、 $\small \Phi _{2}$ 、 $\small \cdots$ 、 $\small \Phi _{k-1}$ 。以下推导过程中出现的 $\small \Phi _{k}$ 不看作单独的参数，而是代表 $\small 1-(\Phi _{1}+\small \Phi _{2}+\cdots +\small \Phi _{k-1})$

y有k个可能的取值：

$\tiny y\in \left \{ 1,2,\cdots ,k \right \}$

T(y)定义为：

$\tiny T\left ( 1 \right )= \begin{bmatrix} 1\\ 0\\ \vdots \\ 0 \end{bmatrix}$ ， $\tiny T\left ( 2 \right )= \begin{bmatrix} 0\\ 1\\ \vdots \\ 0 \end{bmatrix}$ ， $\tiny \cdots$ ， $\tiny T\left ( k-1 \right )= \begin{bmatrix} 0\\ 0\\ \vdots \\ 1 \end{bmatrix}\in {\color{Red} \mathbb{R}^{k-1}}$ ， $\tiny T\left ( k \right )= \begin{bmatrix} 0\\ 0\\ \vdots \\ 0 \end{bmatrix}$

定义T(y)是为了将多项式分布写成指数分布族的形式。这里我们引入一个新的符号叫做指示函数符号，记做 $\tiny I\left \{ true \right \}=1$ ， $\tiny I\left \{ false \right \}=0$ 。该符号用来指示括号中命题的真假，例如 $\tiny I\left \{ 1+1=2 \right \}=1$ 。

$\small T\left ( y \right )$ 是 k=1维向量，所以 $\small T\left ( y \right )_{i}$ 表示第 $\small i$ 个元素，容易得到 $\small T\left ( y \right )_{i}=I\left \{ y=i \right \}$

将多项式分布写成指数分布族的形式：

$\tiny P\left ( y \right )=\Phi _{1}^{I\left \{ y=1 \right \}}\Phi _{2}^{I\left \{ y=2 \right \}} \cdots \Phi _{k}^{I\left \{ y=k \right \}}$

$\tiny = \Phi _{1}^{T\left ( y \right )_{1}}\Phi _{2}^{T\left ( y \right )_{2}}\cdots \Phi _{k-1}^{T\left ( y \right )_{k-1}}\Phi _{k}^{1-\sum_{j=1}^{k-1}T\left ( y \right )_{j}}$

$\tiny = \cdots$

$\tiny =\small b\left ( y \right )e^{\eta ^{T}T\left ( y \right )-a\left ( \eta \right )}$

其中，

$\tiny \eta =\begin{bmatrix} log\left ( \Phi _{1}/\Phi _{k} \right )\\ \vdots \\ log\left ( \Phi _{k-1}/\Phi _{k} \right ) \end{bmatrix}\in \mathbb{R}^{k-1}$ ， $\tiny a\left ( \eta \right )= -log\left ( \Phi _{k} \right )$ ， $\tiny b\left ( y \right )=1$

根据上式推得

$\tiny \Phi _{i}= \frac{e^{\eta_{i} }}{1+\sum_{j=1}^{k-1}e^{\eta _{j}}}$ $\tiny \left ( i=1,2,\cdots k-1 \right )$

$\tiny = \frac{e^{\Theta _{i}^{T}x}}{1+\sum_{j=1}^{k-1}e^{\Theta _{j}^{T}x}}$ $\tiny \left ( \eta _{i}=\Theta _{i}^{T}x \right )$

于是推导出学习算法

$\tiny h_{\Theta }\left ( x \right )= E\left [ T\left ( y \right )|x;\Theta \right ]$

$\tiny = E\left [ \left.\begin{matrix} I\left \{ y=1 \right \}\\ \vdots \\ I\left \{ y=k-1 \right \} \end{matrix}\right|x;\Theta \right ]= \begin{bmatrix} \Phi _{1}\\ \Phi _{2}\\ \vdots \\ \Phi _{k-1} \end{bmatrix}$

$\tiny = \begin{bmatrix} \frac{e^{\Theta _{1}^{T}x}}{1+\sum_{j=1}^{k-1}e^{\Theta _{j}^{T}x}}\\ \vdots \\ \frac{e^{\Theta _{k-1}^{T}x}}{1+\sum_{j=1}^{k-1}e^{\Theta _{j}^{T}x}} \end{bmatrix}$

这个学习算法称作 softmax 回归，它是 logistic 回归的推广

当我们使用 softmax回归来解决问题时：

$\tiny y\in \left \{ 1,2\cdots k \right \}$

对于训练集合

$\tiny \left ( x^{\left ( 1 \right )} ,y^{\left ( 1 \right )}\right )$ ， $\tiny \cdots$ ， $\tiny \left ( x^{\left ( m \right )} ,y^{\left ( m \right )}\right )$

利用极大似然估计（通常情况下，似然性是训练集合中每个样本概率的乘积）求解参数 $\small \Theta$

$\tiny L\left ( \Theta \right )=\prod_{i=1}^{m}P\left ( y^{\left ( i \right )}|x^{\left ( i \right )};\Theta \right )$

$\tiny =\prod_{i=1}^{m}\Phi _{1}^{I\left \{ y^{\left ( i \right )} =1\right \}}\Phi _{2}^{I\left \{ y^{\left ( i \right )} =2\right \}}\cdots \Phi _{k}^{I\left \{ y^{\left ( i \right )} =k\right \}}$ （然后将 $\small \Phi$ 关于 $\small \Theta$ 的表达式代入，这里省略）

接下来对似然函数取对数，然后对 $\small \Theta$ 求导，并利用梯度上升之类的方法求解 $\small \Theta$ 。