何为LCA?LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。
对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。
另一种理解方式是把T理解为一个无向无环图,而LCA(T,u,v)即u到v的最短路上深度最小的点。
计算机竞赛中常常出现结合LCA及各种算法的题目,例如NOIP2015的运输计划、NOIP2013的货车运输等等...
可以说,LCA在近几年算是个热门的考点。如何高效地求LCA也成为了各Oier的关注点。
求解方法
方法一(暴力)
对于有根树T的两个结点u、v,首先将u,v中深度较深的那一个点向上蹦到和深度较浅的点,然后两个点一起向上蹦,直到蹦到同一个点,这个点就是u,v的最近公共祖先,记作LCA(u,v)。
但是这种方法的时间复杂度在极端情况下会达到O(n)。特别是有多组数据求解时,时间复杂度将会达到O(n*m)。
方法二(倍增求LCA)
对于下图我们要求\(u,v\)的LCA,我们首先将\(u,v\)提升至同一高度,然后一起向上跳,直到两点相遇的那一刻,我们就得到了两点的LCA。
但是每次只跳一步的效率太低,我们想要提高算法效率,就必须增大每次跳的步数,这里我们使用倍增。
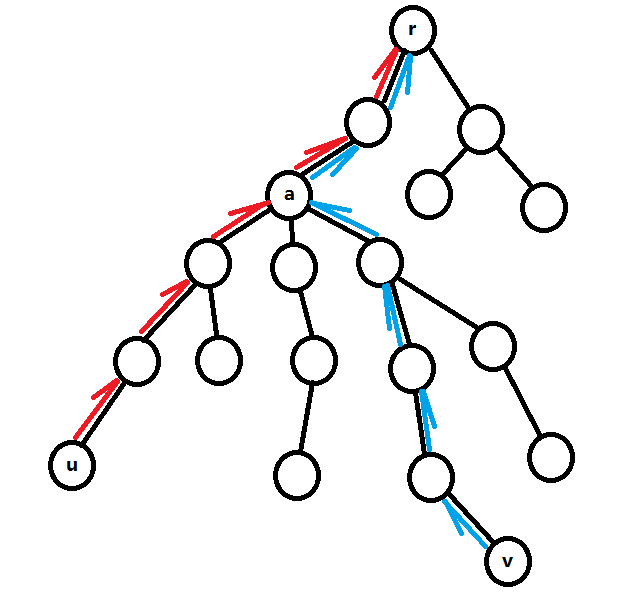
此算法基于动态规划。我们可以先预处理出点i往上跳\(2^j\)步距离到达的点为\(f[i][j]\),则令能够使\(f[u][j]==f[v][j]\)成立的最小的\(j\)对应的\(f[u][j](f[v][j])\)为\(u,v\)两点的LCA。注意:初始化时\(f[i][0]=father[i]\)
举个栗子,例如\(u\)要往上跳6点到达\(r\),则可先跳\(2^2\)到达\(a(a=f[u][2])\),再由\(a\)跳\(2^1\)步到达\(r(r=f[a][1]=f[f[u][2]][1])\)。任何一个数k都可以拆成\(2^i\)的和。
那么,怎么求两个点\(u,v\)的LCA呢?
1:对于\(u和v\)深度比较深的点,假设是\(u\),先把他的深度提到跟\(v\)一样,即一直往他的父节点走。
2:这是\(u和v\)的深度是一样的,然后就一直同时提高\(u,v\)的深度,即一直往他们的父节点走,直到\(u=v\),那么这个点就是\(u和v\)的LCA。
这时,我们已经得出了求两点LCA的方法,只需要将每次提升的步数做修改即可。剩下的我不多说,详细见模板。
模板
void dfs(int now,int fa)
{
f[now][0]=fa; d[now]=d[fa]+1; maxd=max(maxd,d[now]);
for (Re i=head[now];i;i=edge[i].next)
if (edge[i].to!=fa) dfs(edge[i].to,now);
}
int LCA(int u,int v)
{
if (d[u]>d[v]) swap(u,v); int i;
while (d[u]<d[v])
{
for (i=0; d[f[v][i]]>=d[u]; ++i);
v=f[v][i-1];
}
while (u!=v)
{
for (i=1; f[u][i]!=f[v][i]; ++i);
u=f[u][i-1]; v=f[v][i-1];
}
return u;
}
void Initialization()
{
dfs(1,0);
for (int j=1; (1<<j)<=maxd; ++j) //maxd为树的最大深度
for (int i=1; i<=N; ++i)
f[i][j]=f[f[i][j-1]][j-1];
}